计算机组成原理
课程源自B站“湖科大教学匠”的《计算机组成微课堂》 https://www.bilibili.com/video/BV1qG41197E4/?share_source=copy_web&vd_source=440fb90b593ac5ecf9b12f264d73b53b
BV1qG41197E4
1.1 计算机系统的组成
计算机系统分为 硬件 和 软件
其中,硬件包括 主机 和 外设
软件包括 系统软件 和 应用软件
计算机系统性能的好坏,取决于硬件和软件功能的总和
1.2 计算机的发展
第一台真正意义上的电子数字计算机 :ABC
第一台实用的电子数字计算机 :ENIAC
计算机硬件的发展 :电子管计算机 -> 晶体管计算机 -> 集成电路计算机 -> 超大规模集成电路
计算机软件的发展 :机器语言 -> 汇编语言 -> 高级语言 -> 面向对象
1.3 计算机硬件
冯诺依曼计算机主要特点 :
- 构成程序的指令和数据均采用 二进制 表示
- 指令和数据存放在存储器 中,按地址访问
- 指令 在存储器中 按顺序存放 ,一般情况下,指令是 顺序执行 的
- 指令由 操作码 和 地址码 组成
- 机器 以运算器为中心 ,输入输出设备与存储器间的数据传送通过运算器完成
- 计算器硬件由 运算器、控制器、存储器、输入输出设备 组成
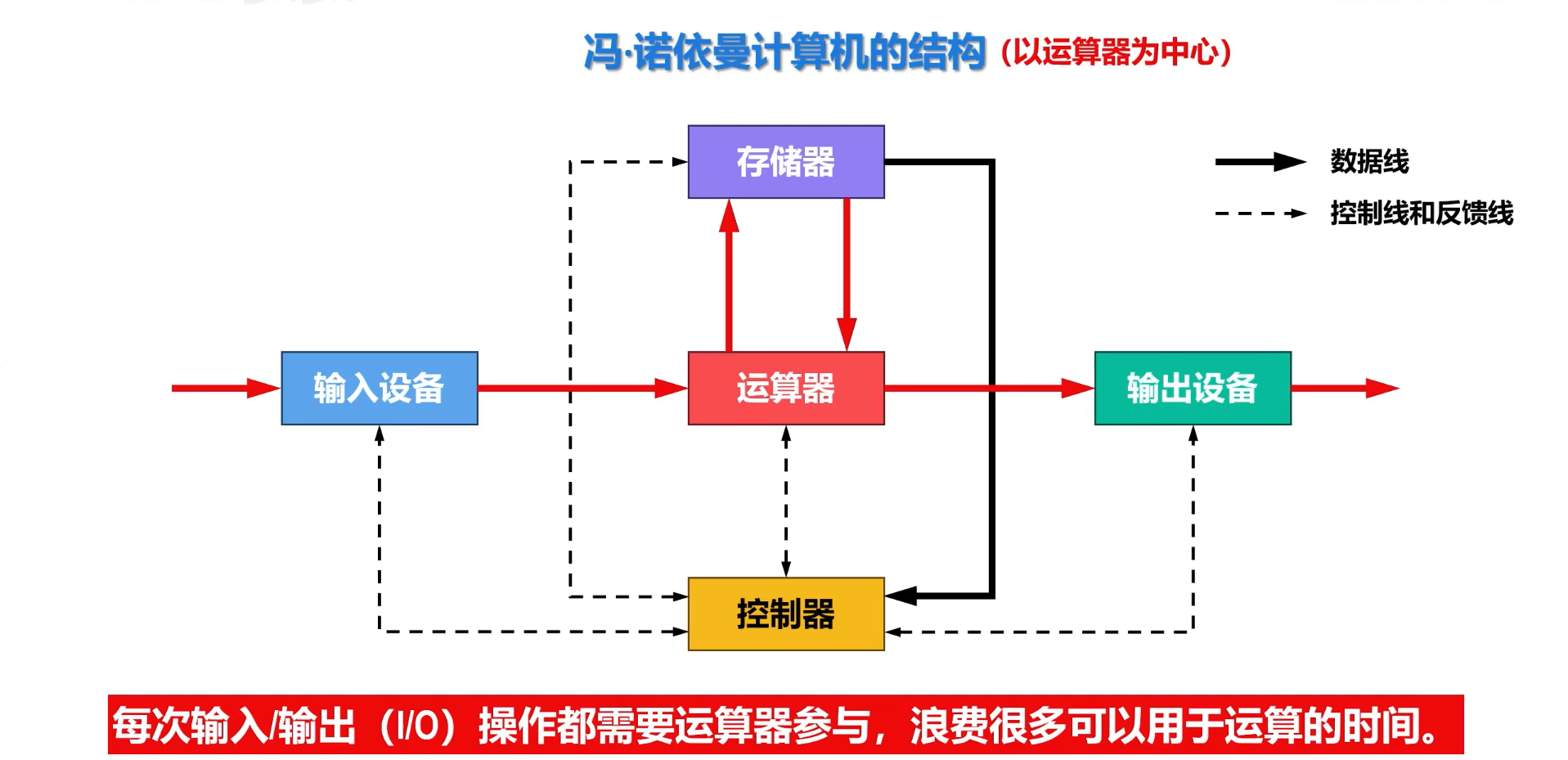
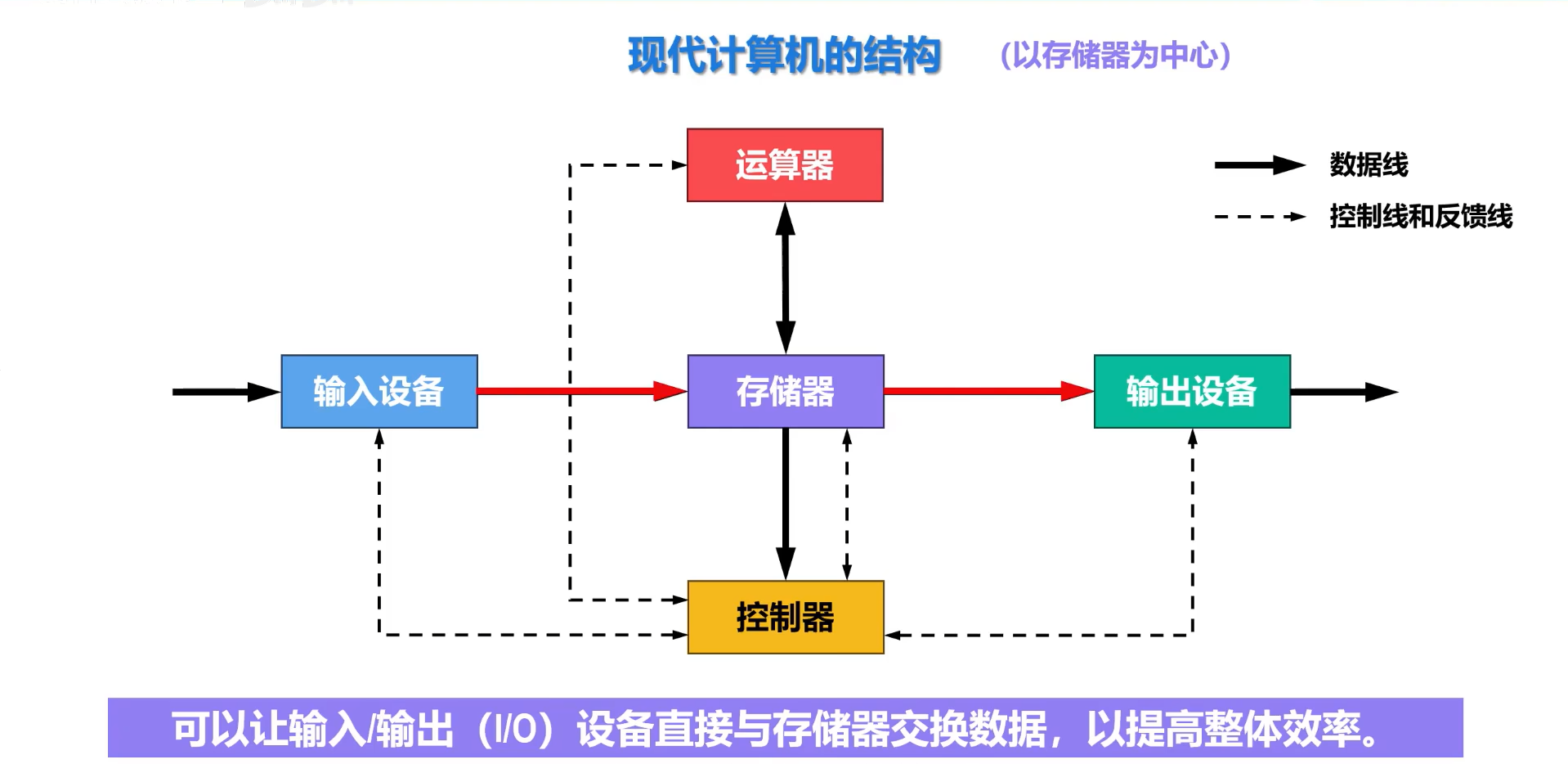
其中,存储器分为 主存储器 和 辅助存储器
主存储器:用于存放程序和数据,可以 直接与CPU交换信息 ,又称为内存储器,简称内存或主存。
辅助存储器:用于帮助主存存储更多的信息。又称外部存储器,简称为外存或辅存。 储存中的信息必须调入主存后,才能被CPU访问 。
运算器 的核心为 算术逻辑单元ALU ,主要功能有算术运算和逻辑运算。
1.4 计算机软件
分为 系统软件 和 应用软件
计算器软件的发展:
-
用机器语言编程
使用 机器指令的二进制编码 编写程序
编程繁琐,易出错且不易排错
计算机可以直接识别和执行
-
用汇编语言编程
使用 表示机器指令的特殊符号 编写程序
相比于用机器语言编写,汇编语言这种符号语言简单直观,便于记忆
计算机不能识别和执行 用汇编语言编写的程序,须通过汇编器翻译成机器语言程序
-
用高级语言编程
使用 规定好的一套基本符号和编程规则
直观通用, 与具体机器无关
计算机不能识别和执行 用高级语言编写的程序,须通过编译器翻译成汇编语言或机器语言
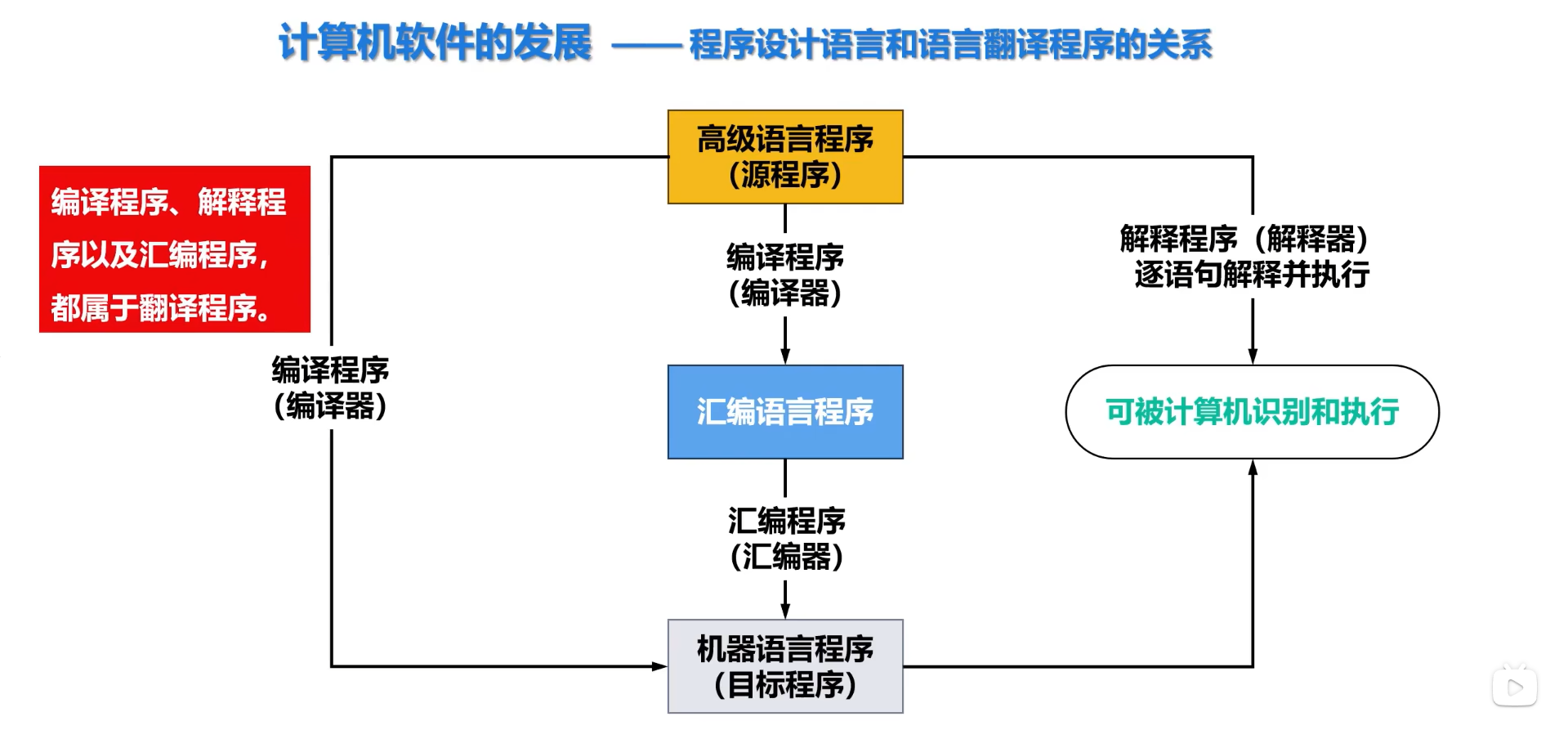
将高级语言程序转换成可执行目标程序的主要过程:
预处理 -> 编译 -> 汇编 -> 链接
随着硬件和软件的不断发展,人们又创造出了一类程序,称为 操作系统
操作系统提供了在 汇编语言和高级语言的使用和实现过程中所需的某些基本操作 。
操作系统负责 控制并管理计算机系统全部硬件资源 (例如CPU、内存和外部设备)和 软件资源 (例如编译程序、应用程序等)。
1.5 计算机系统的层次结构
| 层次 | 描述 | 说明 |
|---|---|---|
| 第 6 层 | 高级语言层 | 使用与机器无关的高级语言编程,无需掌握机器的底层技术细节,只要掌握某种高级语言的语法规则以及算法和数据结构等方面的知识进行编程。 |
| 第 5 层 | 汇编语言层 | 使用汇编语言进行编程。由于汇编语言的每条语句都与机器语言的某条语句对应,因此仍要求程序员对实际机器的内部组成和指令系统非常熟悉。 |
| 第 4 层 | 操作系统层 | 设计人员不仅要对操作系统的设计理论有比较深入的理解,还需要掌握具体机器的指令集和汇编语言以及适于编写操作系统软件的高级语言。 |
| 第 3 层 | 指令集体系结构层 ISA | 定义了某计算机可执行的所有机器指令的集合,规定了对于每条机器指令计算机应执行什么操作,所处理的操作数应存放的位置以及操作数的类型等。 |
| 第 2 层 | 微程序层 | 将一条机器指令编写成一个微程序。每个微程序包含若干条微指令,每条微指令对应一条或多条微操作。 |
| 第 1 层 | 逻辑电路层 | 计算机硬件系统的底层,由逻辑门、寄存器等逻辑电路组成。 |
1.6 计算机的基本工作原理
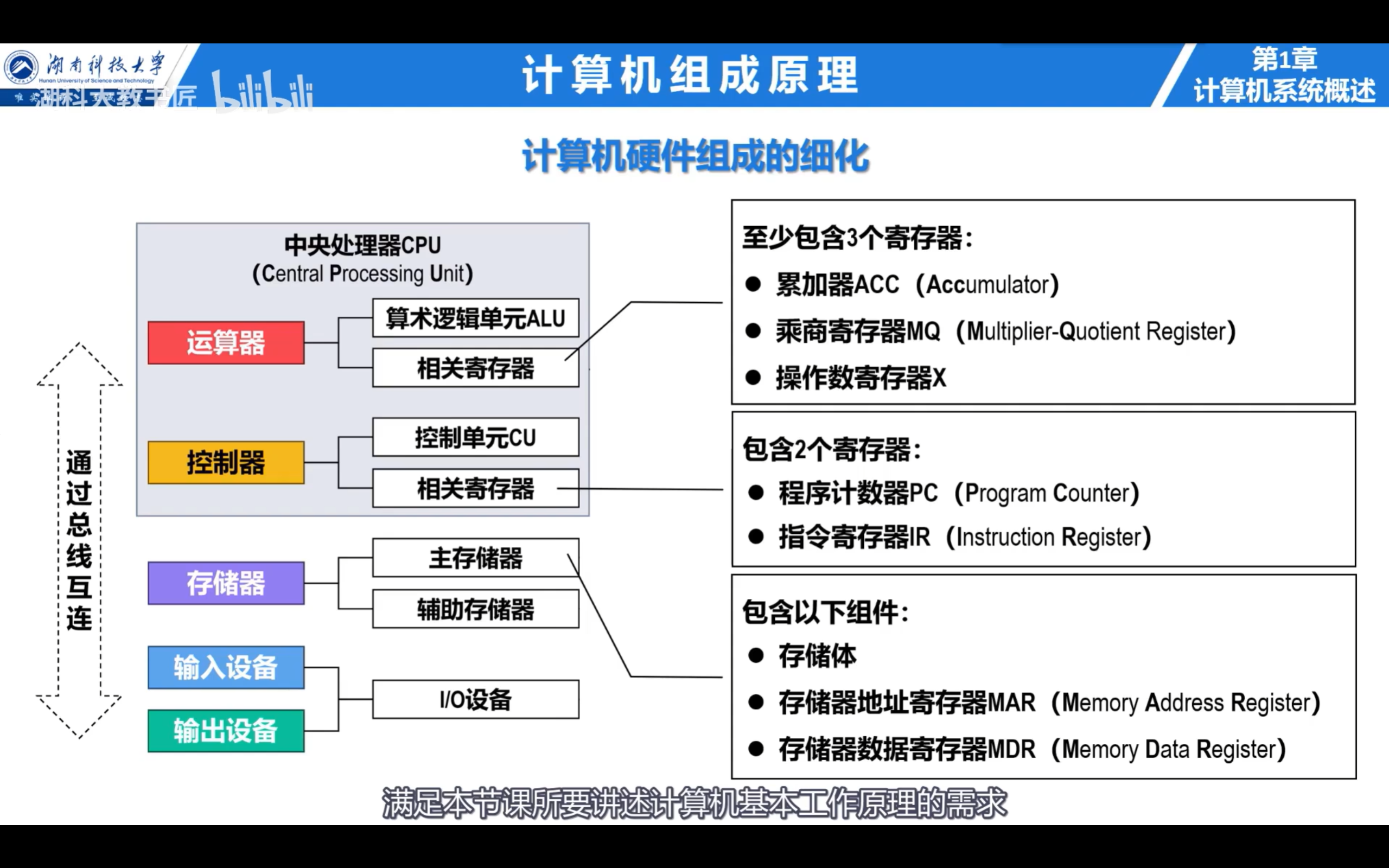
运算器
| ALU | 加 | 减 | 乘 | 除 |
|---|---|---|---|---|
| ACC | 被加数和 | 被减数差 | 乘积高位 | 被除数余数 |
| MQ | 乘数 乘积低位 | 商 | ||
| X | 加数 | 减数 | 被乘数 | 除数 |
- ACC 表示累加器
(ACC)表示累加器中的内容- MQ 表示乘商寄存器
(MQ)表示乘商寄存器中的内容- X 表示操作数寄存器
(X)表示操作数寄存器中的内容- M表示主存储器中某个存储单元的地址
(M)表示地址为M的存储单元中的内容
加法操作过程:
- (M)→X
取出存放在主存中地址为M的存储单元中的内容(M)(加数),送到操作数寄存器X中 - (ACC) + (X) → ACC
将累加器ACC中的内容(ACC)(被加数)与操作数寄存器X中的内容(X)(加数)相加,结果(和)保留在累加器ACC中
减法操作过程:
- (M)→X
取出存放在主存中地址为M的存储单元中的内容(M)(减数),送到操作数寄存器X中 - (ACC) - (X) → ACC
将累加器ACC中的内容(ACC)(被减数)与操作数寄存器X中的内容(X)(减数)相减,结果(差)保留在累加器ACC中
乘法操作过程:
- (M)→MQ
取出存放在主存中地址为M的存储单元中的内容(M)(乘数),送到乘商寄存器MQ中 - (ACC)→X
将累加器ACC中的内容(ACC)(被乘数),送到操作数寄存器X中 - (X) × (MQ)→ACC // MQ
将操作数寄存器X中的内容(X)(被乘数)与乘商寄存器MQ中的内容(MQ)(乘数)相乘,结果(积)的高位保留在累加器ACC中,低位保留在乘商寄存器MQ中
除法操作过程:
-
(M)→X
取出存放在主存中地址为M的存储单元中的内容(M)(除数),送到操作数寄存器X中 -
(ACC) ÷ (X) → MQ
将累加器ACC中的内容(ACC)(被除数)除以操作数寄存器X中的内容(X)(除数),结果(商)保留在乘商寄存器MQ中,余数保留在累加器ACC中。
存储器
存储体 由很多个 存储单元 组成
每个 存储单元 由若个 存储元件 组成
每个存储元件能存储一位 二进制数"0"或"1"
一个存储单元中可存储一串二进制信息,称这串二进制信息为一个 存储字 ,这串 二进制信息的位数 称为 存储字长
给每个存储单元都赋予一个编号,称为 存储单元的地址
存储器 地址寄存器 MAR ,用来 存放欲访问的存储单元的地址
MAR的位数 ,决定了 存储单元的数量
存储器 数据寄存器MDR ,用来 存放从存储体的某个存储单元取出的信息或者准备往某个存储单元存入的信息
MDR的位数(长度) ,与 存储字长相等 。
主存(内存)的这种按存储单元的地址来实现对其写入和读取的存取操作,需要在CPU中的控制器的控制下进行。
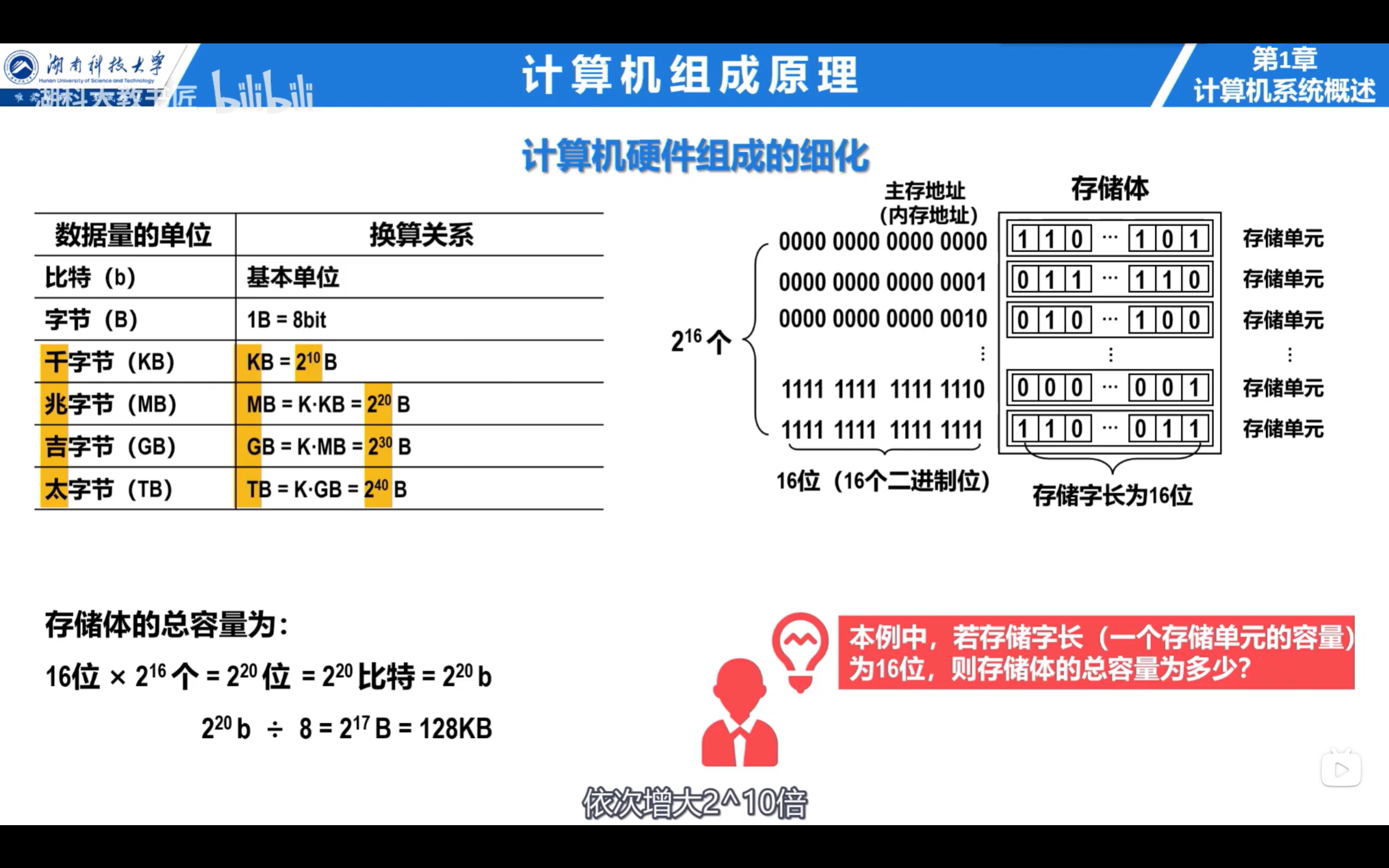
控制器
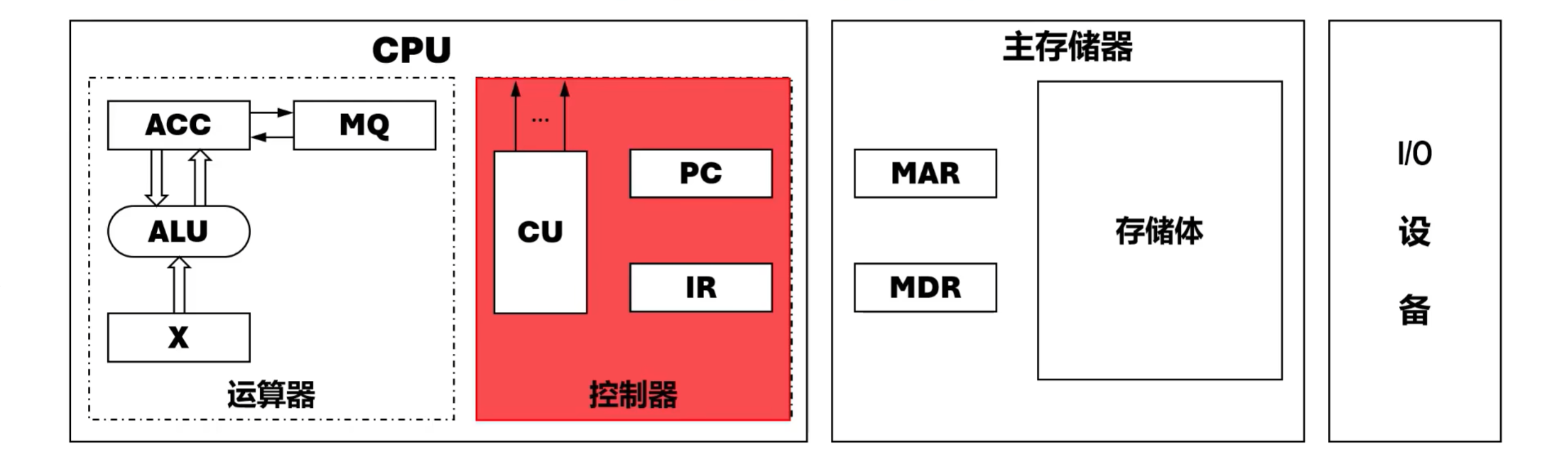
控制器是计算机的神经中枢,由它指挥各部件自动、协调地工作。
- 控制从主存中读取一条指令,称为 取指 过程(阶段)。
- 对指令进行分析,指出该指令要完成何种操作,并按寻址特征指明操作数的地址,称为 分析 过程(阶段)。
- 根据指令的操作码和操作数所在的地址完成某种操作,称为 执行 过程(阶段)。
程序计数器PC 用来 存放当前欲执行指令的地址
-
PC与MAR 之间有一条直接通路。
-
PC自动形成 下一条指令的地址 “自动加1”功能)
指令寄存器IR 用来存放当前的指令
-
IR的内容来自MDR。
-
IR中的 操作码 (用OP(IR)表示)会送至CU(用 OP(IR)→CU 表示),用来 分析指令 。
-
IR中的 地址码 (用Ad(IR)表示)作为操作数的地址送至MAR(用 Ad(IR)→MAR 表示),用来 从内存中取操作数 。
控制单元CU 用来 分析当前指令所需完成的操作,并发出各种微操作命令序列 ,用以控制所有被控对象。
机器指令简介
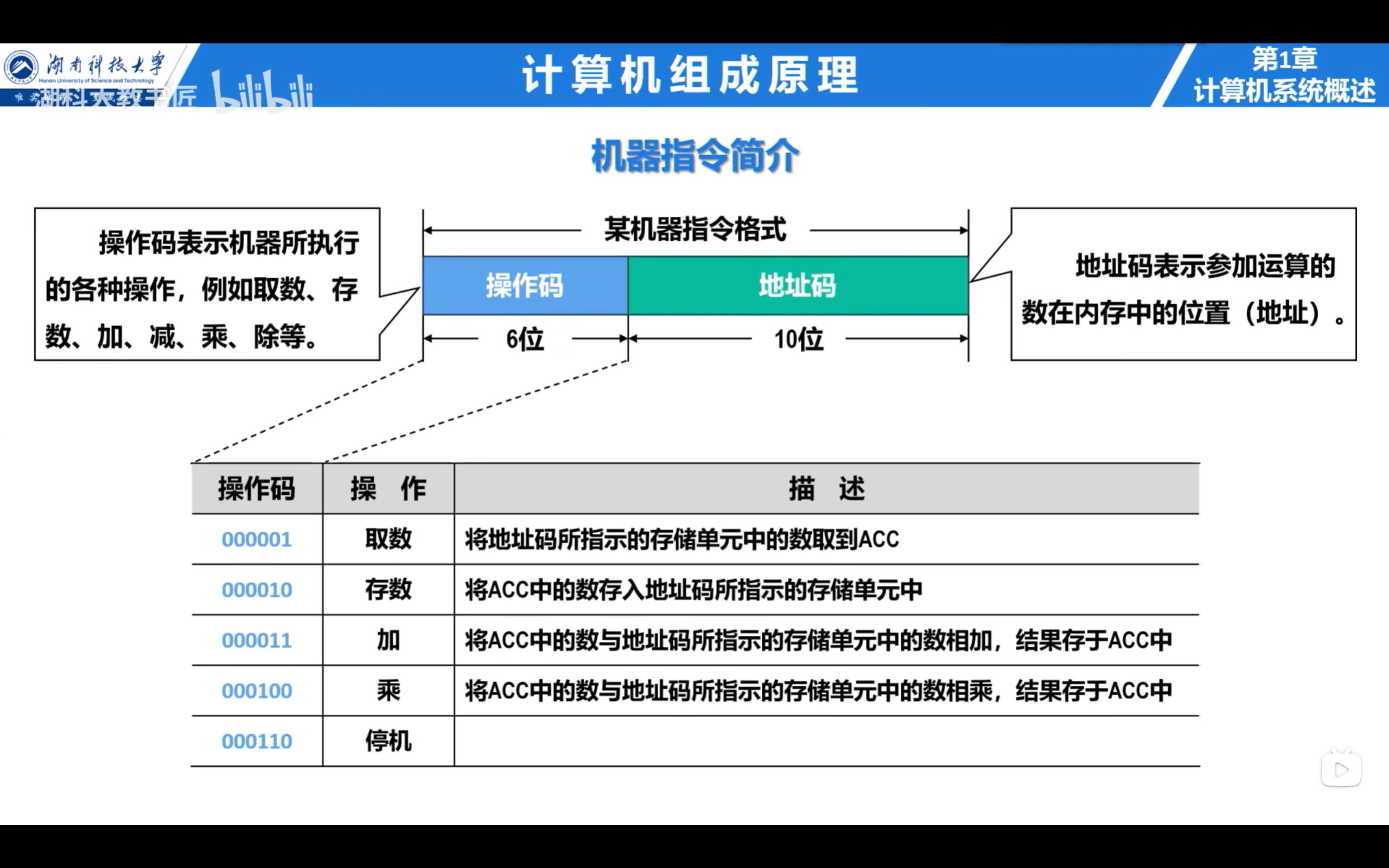
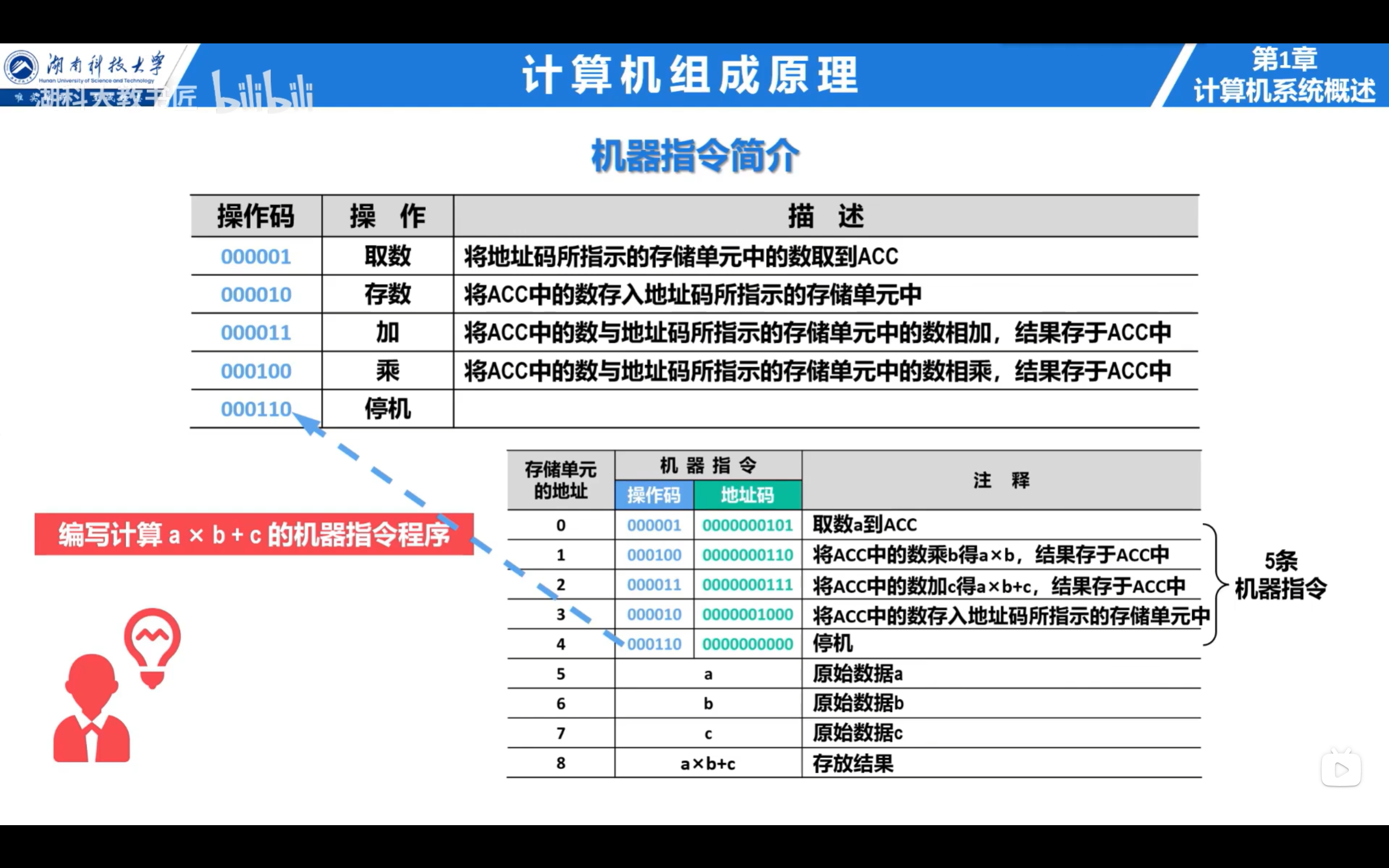
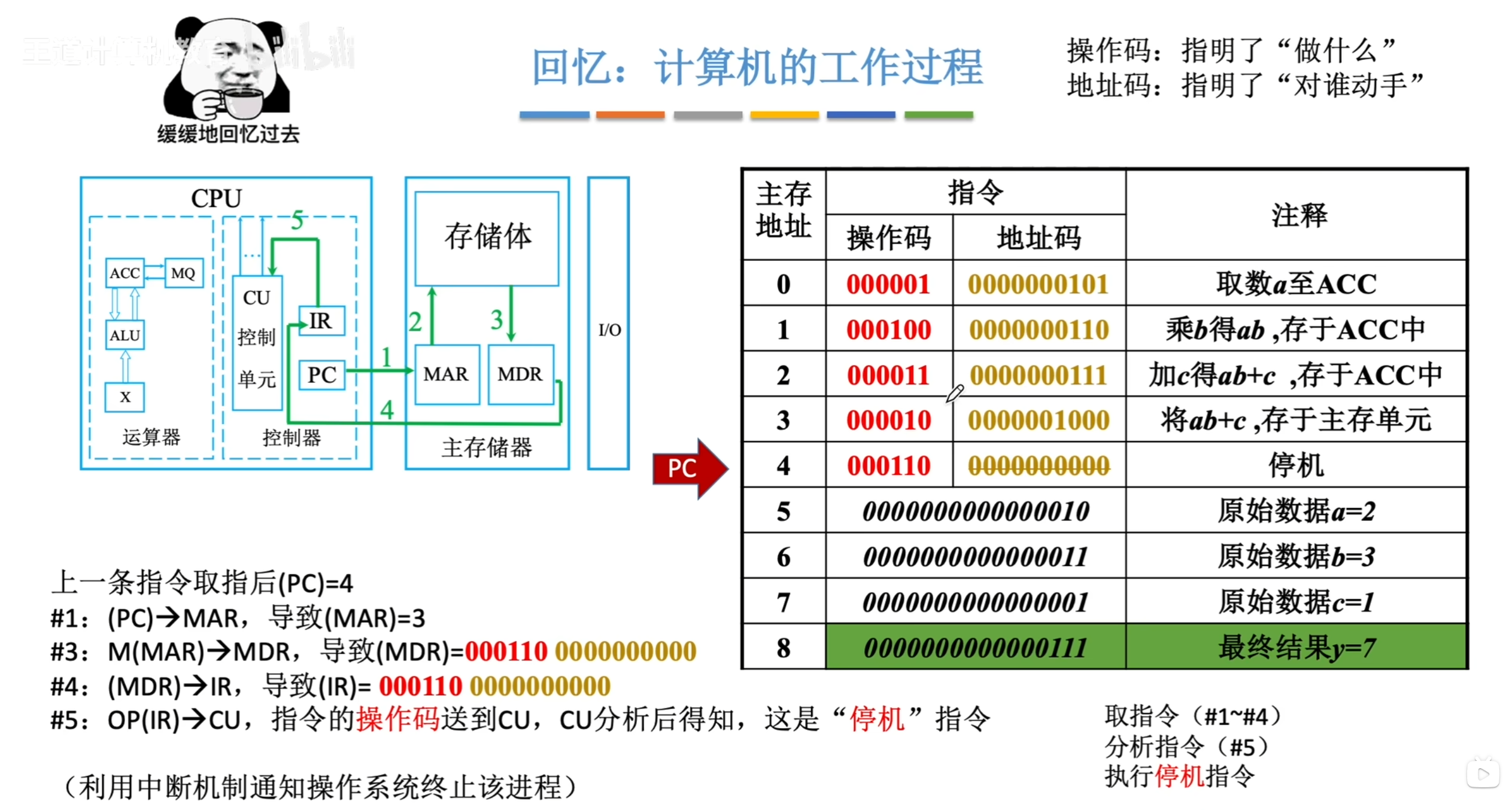
计算机的基本工作原理
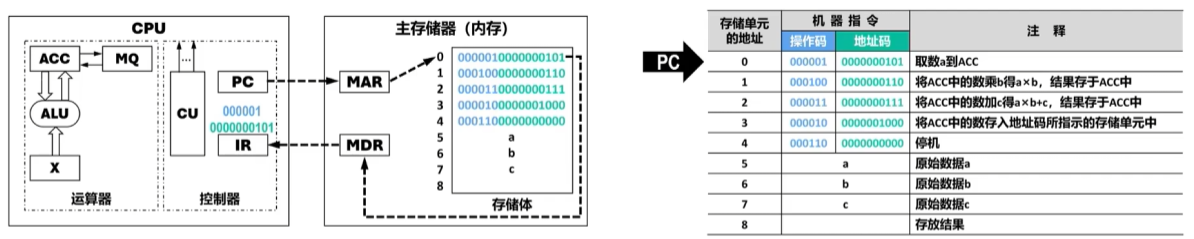
初始化:(PC)=0,指向内存中的编号为0的存储单元,该存储单元的内容是第一条机器指令
对第一条指令进行 取指 :
- 控制器将PC的内容送至内存的MAR(用(PC)→MAR表示)对内存进行寻址,并命令内存做读操作,此时所寻址的存储单元(0号存储单元)的内容“0000010000010101”被送入MDR内。
- 将MDR的内容传送至控制器的IR(用(MDR)→IR表示)。
接下来,程序计数器PC中的值从0自动增加到了1,在完成对第一条指令的取指操作后,对该指令进行 分析
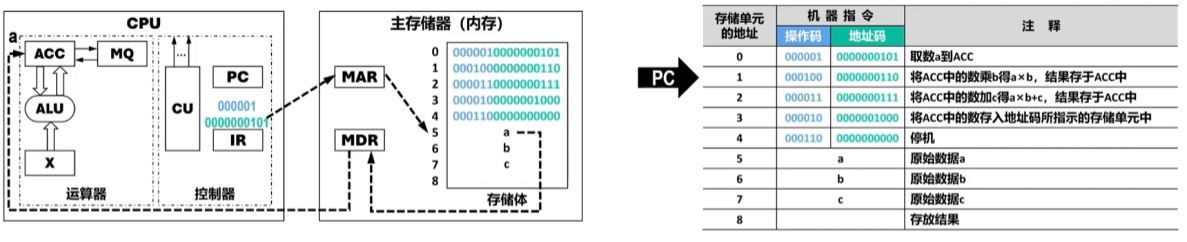
对第一条指令进行 执行 :
- 将IR中保存的指令的地址码送至MAR(用Ad(IR)→MAR)对内存进行寻址,并命令内存做读操作,此时所寻址的存储单元(“0000000101”号存储单元,即5号存储单元)的内容“a”被送入MDR内。
- 将MDR的内容传送至运算器的ACC(用(MDR)→ACC表示)。
例题
【习题3】存放当前指令的寄存器是(C)。
A. PC B. MDR C. IR D. MAR
【习题4】用来存放当前欲执行指令的地址的寄存器是(B)。
A. IR B. PC C. MAR D. CU
解析:
- 指令寄存器IR用来存放 当前的指令
- IR的内容来自存储器数据寄存器MDR。
- 程序计数器PC用来存放 当前欲执行指令的地址
- PC与存储器地址寄存器MAR之间有一条直接通路。
- PC自动形成下一条指令的地址(“自动加1”功能)
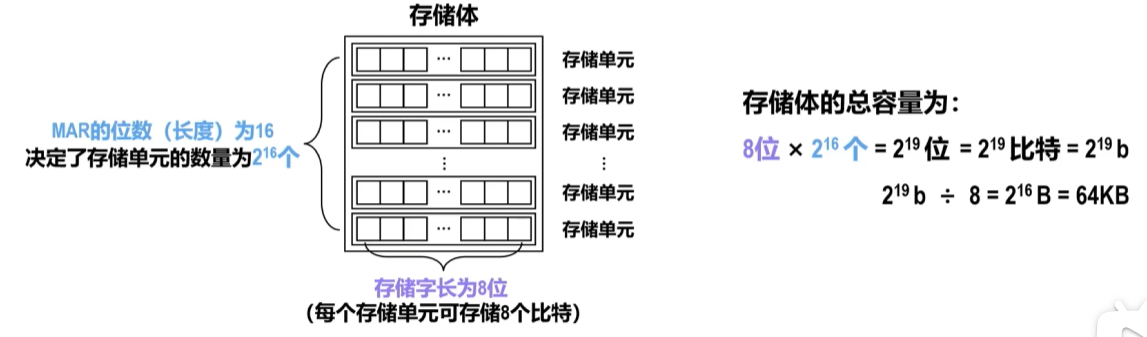
【习题7】若存储字长为8位,MAR的位数为16位,则存储体的总容量为(B)。
A.128B B.64KB C.128KB D.256KB
解析:
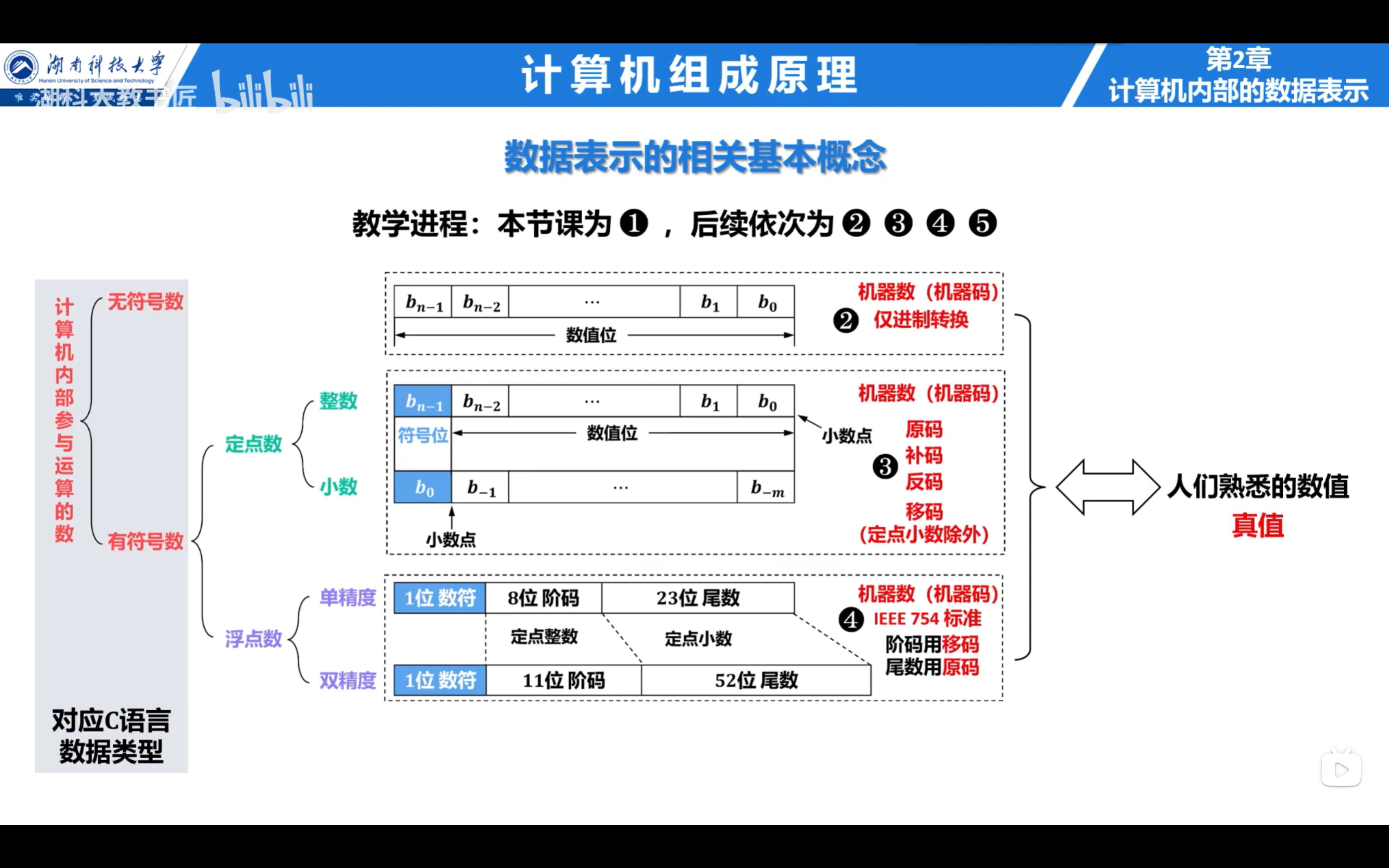
2.1 数据表示的相关基本概念
数字分类:
- 无符号数:3238264832
- 有符号数:-1056702464(整数)、-0.491943359375(纯小数)、-8.25(带小数)
数字表示方式:
- 整数:小数点位置固定
- 纯小数:小数点位置固定
- 定点数:小数点位置固定
- 浮点数:小数点位置浮动
2.2 进位计数制及其数据之间的相互转换
常用的进位计数制有十进制、二进制、八进制、十六进制
任意进制->十进制

常用进制数对照表
| 十进制 | 二进制 | 八进制 | 十六进制 |
|---|---|---|---|
| 0 | 0000 | 0 | 0 |
| 1 | 0001 | 1 | 1 |
| 2 | 0010 | 2 | 2 |
| 3 | 0011 | 3 | 3 |
| 4 | 0100 | 4 | 4 |
| 5 | 0101 | 5 | 5 |
| 6 | 0110 | 6 | 6 |
| 7 | 0111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
二进制->其他进制
3位二进制数 ↔ 1位八进制数
举例:
- 二进制:
- 转换为八进制:
转换过程:
-
将二进制数按每 三位一组 进行分组:
小数部分:110 110(后面少位则补零)
整数部分:001 011 001 100(前面少位则补零)
4位二进制数 ↔ 1位十六进制数
举例:
- 二进制:
- 转换为十六进制:
转换过程:
-
将二进制数按每 四位一组 进行分组:
小数部分:1101 1000
整数部分:0010 1100 1100
十进制->任意进制

2.3.1 原码
符号位 ,值为 0表示正数,1表示负数
数值位 (二进制),为真值的绝对值
原码表示又称为 带符号的绝对值表示
定点整数的原码定义
假设真值 x 为 定点整数 ,n 为 x 的原码表示中数值位的位数(比特数量):
假设真值 ,,x的原码表示中符号位为 (其位权值为 24)。
= 24 + | | = = 10000 + = 1,
举例:
x = +1110 则
x = -1110 则
须注意 第一位的1是负数 的含义
定点小数的原码定义
假设真值x为定点小数:
举例:
x = +0.1101 则
x = -0.1101 则
原码的特点
原码在计算机中目前仅仅用于表示浮点数的尾码
优点:
- 表示方法简单直观
缺点:
-
真值0 在原码中 有两种不同的表示
-
-
符号位不能直接参与运算
2.3.2 补码
将补数的概念应用到计算机内部,便出现了补码这种机器码(机器数)。
- 正数的补码:符号位为0,数值位是它本身。
- 负数的补码:等于 模数加上该负数本身 ,而模数就是最高位进位的位权值。
补数
-
模的概念
- 模 (或称模数)是一个数值计量系统的 计量范围 ,记作mod或M。
- 只要确定了“模”,就可找到一个 与负数等价的正数 来代替此负数,该正数就是负数的 补数 。
- 超过计量范围的数都应该自动舍弃模数 。
-
补数的特点
- 一个负数可用它的正补数来替代,而这个正补数可以用 模数加上负数本身 求得。
- 一个正数和一个负数 互为补数时,它们的绝对值之和即为模数 。
- 正数的补数即该正数本身 。
-
寻找一个负数的正补数的意义
- 把减法运算用加法实现
- 符号位也可以直接参与运算
举例:设 A = 9 , B = 5 , 求 A - B , (mod 12)
作加法运算:A - B = + = + = 9 + (模数 + (-5)) = 9 + (12 + (-5)) = 16 = 4
定点整数的补码定义
假设真值为定点指数,为的补码表示中首位位的位数(比特数),为的补码表示中数值位的位数(比特数),加上1个符号位,的补码表示共有 位,最低位的位权值为 ,而最高位(符号位)的位权数为 ,因此最高位进位的位权值为值为 ,即 模数为 。
【举例】 某计算机的字长为8位,真值为定点整数 , 求。
模数为 2⁸ ,
定点小数的补码定义
假设真值为定点小数(纯小数),小数点在左侧的位为最高位(符号位),其位权值为 ,而最高位进位的位权值为,即 模数为 。
【举例】
现代计算机中多采用IEEE 754标准表示浮点数,而其中的 定点小数采用原码表示 ,因此通常 不会涉及设计定点小数的补码表示 。
补码的特点
目前计算机中普遍采用补码表示有符号定点整数,例如C语言中char,short,int,long型整数都是采用补码进行表示的。
优点:
- 补码表示方法使得减法运算可以转换成加法运算。
- 真值0在补码中只有一种表示,这使得补码比原码多表示一个最小负数。
- 符号位可以直接参与运算,运算时符号位的进位作为模会被自动舍弃。
缺点:
- 补码的表示相对原码更加复杂
- 原码的数值位与真值的绝对值相同。因此,通过原码可以很容易地得出真值。但是,补码就没有这么简单了。
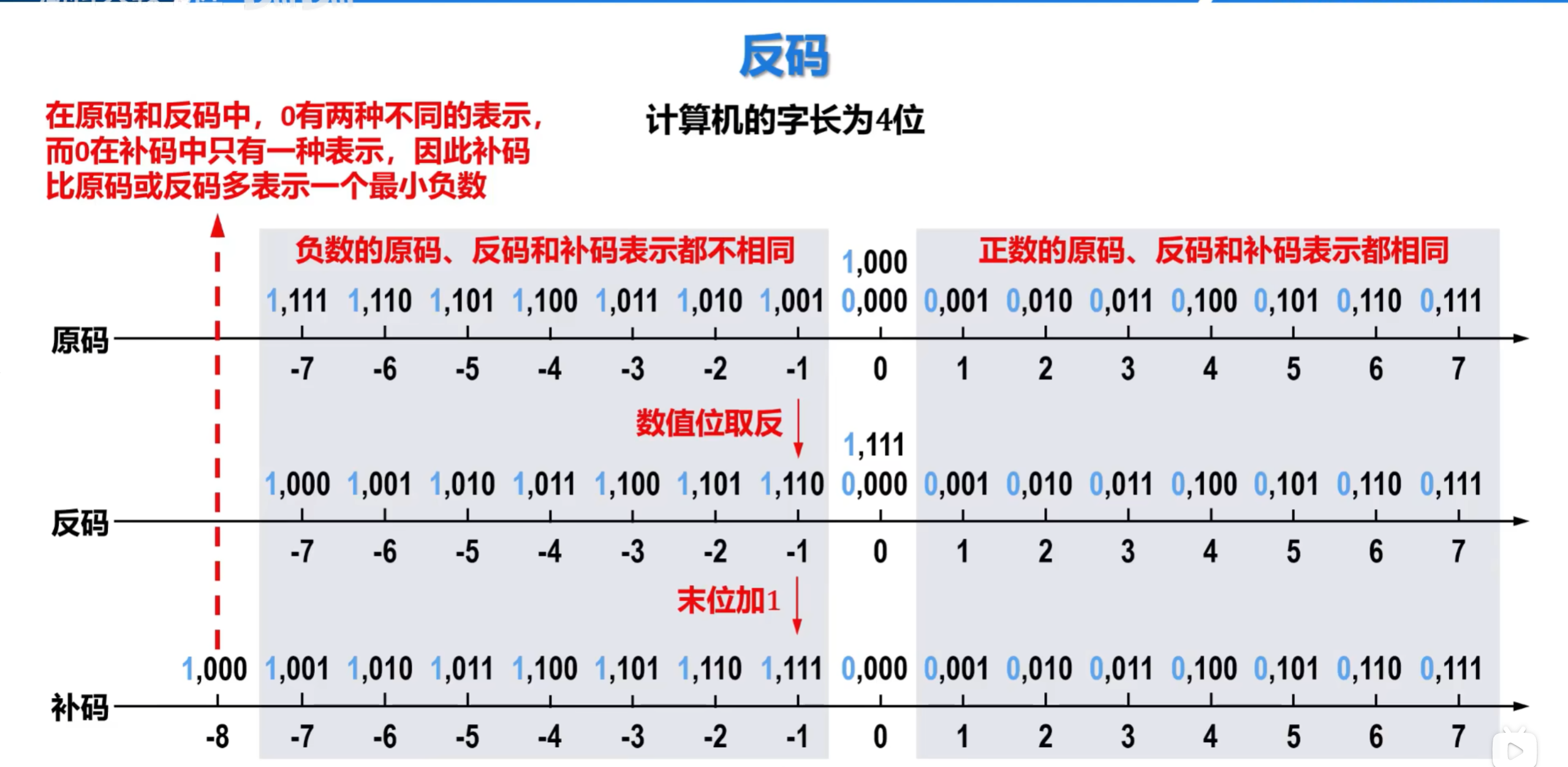
2.3.3 反码
反码通常用来作为有原码求补码或者由补码求原码的 中间过渡
- 正数的反码:符号位为0,数值位就是它本身。
- 负数的反码:符号位为1,数值位就是真值数值位取反。
原码->反码->补码
原码的符号位不变,数值位取反,之后末位加一
| 真值 | 原码 | 取反说明 | 反码 | 加1说明 | 补码 |
|---|---|---|---|---|---|
| -1 | 1,001 | 符号位不变,数值位取反 | 1,110 | 末位加1 | 1,111 |
| -2 | 1,010 | 符号位不变,数值位取反 | 1,101 | 末位加1 | 1,110 |
| -3 | 1,011 | 符号位不变,数值位取反 | 1,100 | 末位加1 | 1,101 |
| -4 | 1,100 | 符号位不变,数值位取反 | 1,011 | 末位加1 | 1,100 |
| -5 | 1,101 | 符号位不变,数值位取反 | 1,010 | 末位加1 | 1,011 |
| -6 | 1,110 | 符号位不变,数值位取反 | 1,001 | 末位加1 | 1,010 |
| -7 | 1,111 | 符号位不变,数值位取反 | 1,000 | 末位加1 | 1,001 |
定点整数的反码定义
假设真值位定点整数,为的反码表示中数值位的位数(比特数量)。
【举例】
定点小数的反码定义
假设真值为定点小数,为的反码表示中数值位的位数(比特数量)。
【举例】
【练习】
反码的特点
反码在计算机中目前很少被使用
优点:
- 符号位可以参与运算
缺点:
- 最高位(符号位)产生的进位要加到运算结果的低位(循环进位)
- 真值0在反码中由两种不同的表示
2.3.4 移码
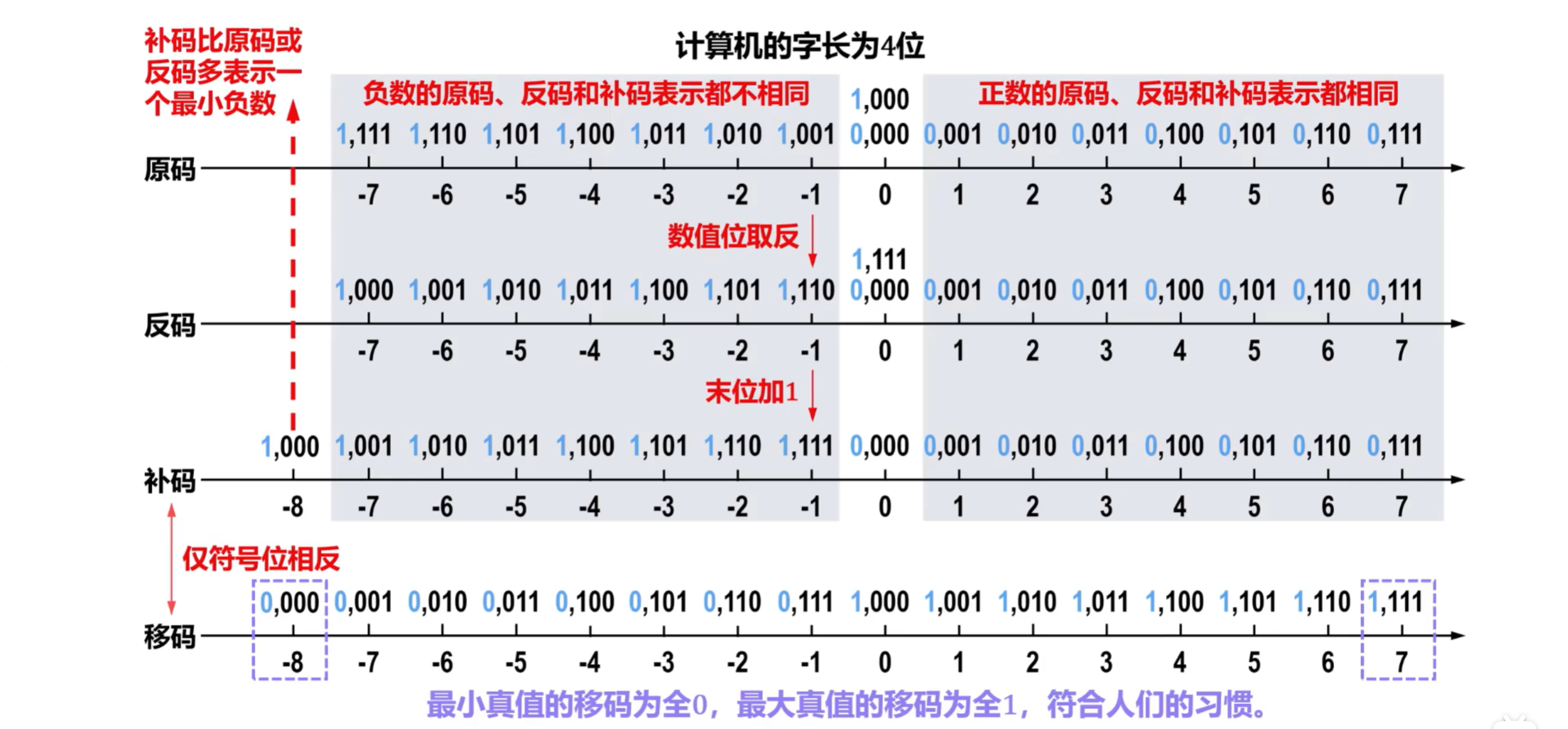
移码就是在 **真值上加一个常数 **
- 在数轴上,移码所表示的范围对应于真值在数轴上的范围 向轴的正方向移动个单元
- 移码 只用于定点整数 的表示
移码定义
假设真值为定点整数, 为 的移码表示中数值位的位数(比特数量)
【举例】
移码的特点
优点;
- 真值0 在移码中只有 一种表示 。
- 移码保持了 真值原有的大小顺序 ,可以直接比较大小。
- 最小真值的移码为全0,最大真值的移码为全1,符合人们的习惯。
- 当浮点数的阶码用移码来表示时,就能很方便地比较阶码的大小。
2.3.5 定点数的编码间的相互转化
原码和补码互为补码,补码的补码是原码
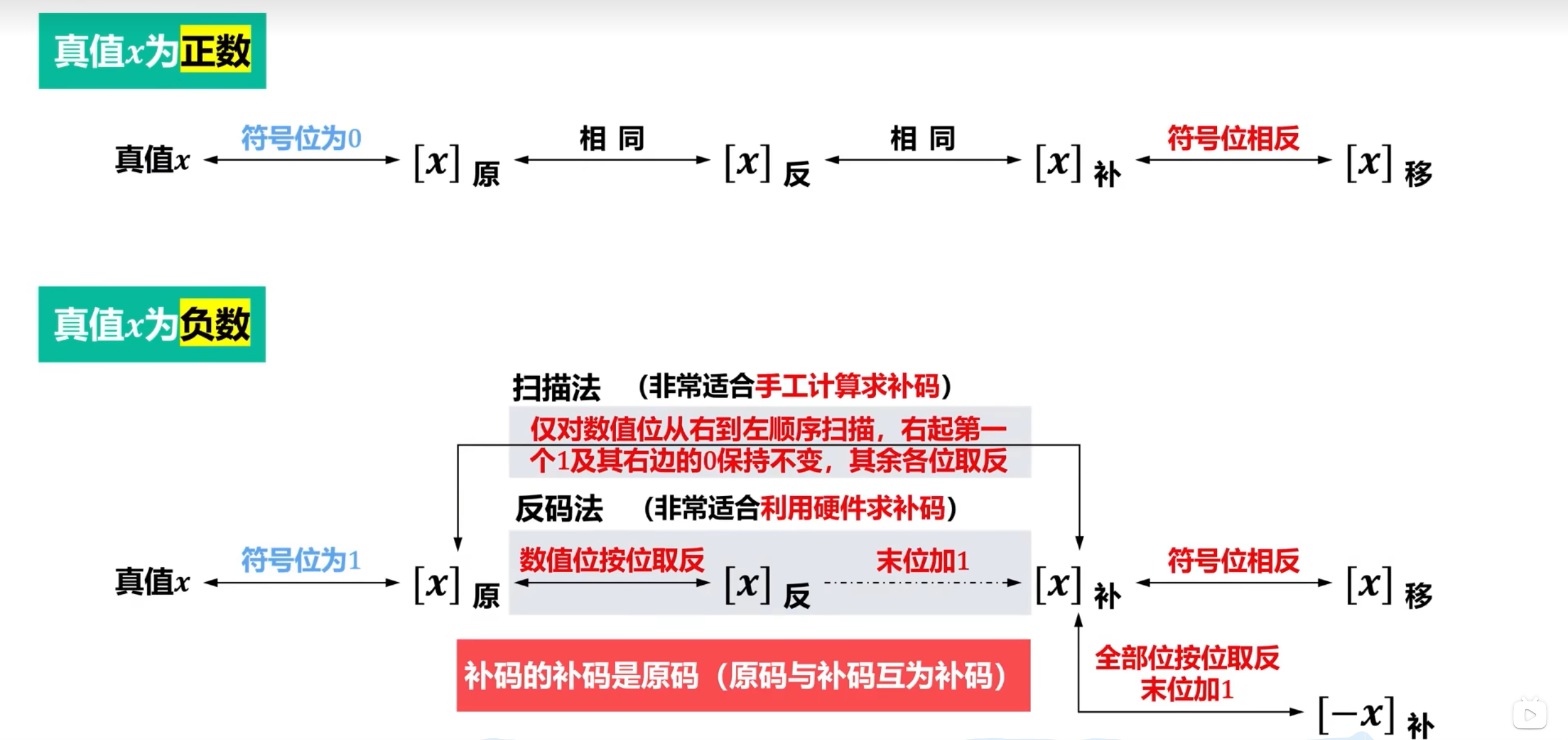
仅对数位值 从右到左 顺序扫描,右起第一个1及其右边的0保持不变,其余各位取反(也可以反过来从补码求原码)
【举例】
原码 从右到左,也就是最右侧 的部分不变,而剩下的数值位上的数字均取反,即 这部分取反,最后可得补码为
再者,若已知 求 ,则可以先将 全部位 按位取反,然后 末位加1
已知原码、反码、补码,如何算出真值(十进制形式):
-
正数:
将原码、反码、补码的数值位按权展开相加,符号位的0表示“+”。 -
负数:
将反码、补码转换成原码,然后将原码的数值位按权展开相加,符号位的1表示“-”。
2.3.6 定点数的编码——习题课
【习题1】对真值0具有唯一表示形式的机器数是( C )
- A. 原码 B.补码和反码 C.移码和补码 D.以上都不对
0的数量 取决于机器字长
原码 反码 补码 移码 [+0] 0,000…0 0,000…0 0,000…0 1,000…0 [−0] 1,000…0 1,111…1 0,000…0 1,000…0
【习题2】8位原码能表示的不同的数据的量是( C )
- A.127 B.128 C.255 D.256
8位原码应共有 个组合,但0在原码中有[+0]和[-0]两种表示(见上题),算是重复的数据
【习题3】某机器字长为8位,机器码采用补码,则机器码所能表示的范围是( B )
- A. -127 ~ +127 B. -128 ~ +127 C. -128 ~ +128 D.以上都不对
补码(二进制) 十进制值 说明 0000 0000 0 0000 0001 +1 0000 0010 +2 0000 0011 +3 … … 0111 1111 +127 最大值 1000 0000 -128 最小值 1000 0001 -127 1000 0010 -126 1000 0011 -125 … … 1111 1111 -1
【习题4】若 , 则 是( D )
- A. 0,1001011 B. 0,1001100 C. 1,1001011 D. 1,1001100
详见2.3.5的 原码<->补码 扫描法
【习题5】若 , 则 是( D )
- A. +75 B. +76 C. -75 D. -76
先转化为原码,再将二进制原码转化为十进制数(注意第一位的符号位)
【习题6】设机器码采用补码形式,若寄存器内容为9BH,则对应的十进制数是( C )
- A. -27 B. -97 C. -101 D. 155
H表示为16进制数,即
十六进制转为二进制,1个数转换成4个数
则原码为
【习题7】假定十进制数为-66,按补码形式存放在一个8位寄存器中,该寄存器的内容用十六进制表示为( B )
- A. C2H B. BEH C. BDH D. 42H
【习题8】已知 , 则 是( B )
- A. 0,1001011 B. 0,1001100 C. 1,1001011 D. 1,1001100
详见2.3.5
【习题9】已知 , 则 是( D )
- A. 0,1111111 B. 0,0000001 C. 1,0000000 D. 无法表示
所以
然而8位定点整数补码能表示的最大正数为 , 128无法用8位补码表示,结果溢出
若是用2.3.5的全取反再加1的方法,可得 成了正数相加为负数,结果溢出
【2015考研 题13】由3个1和5个0组成的8位二进制补码,能表示的最小整数是( B )
- A. -126 B. -125 C. -32 D. -3
首先要用一个1放在符号位取负,另外两个一,按照原码补码转换方法反向思考,将它们放到最低位,组成 , 接下来再转换,可得
【2021考研 题13】已知带符号整数用补码表示,变量 的机器数分别为
下列结论中,正确的是( D )
-
A. 若和为无符号整数,则
-
B. 若和为无符号整数,则
-
C. 若和为带符号整数,则
-
D. 若和为带符号整数,则
无符号整数可以直接比较大小,
带符号整数则要写成二进制形式:
【2022考研 题13】32位补码所能表示的整数范围是( B )
- A. ~ B. ~ C. ~ D. ~
以8位补码为例,最小值是 最大值是
2.4.1 浮点数的表示形式和表示范围
定点小数
┌──────┬──────┬──────┬──────┬─────┬──────┐ |
| 原码 | 反码 | 补码 | ||||
|---|---|---|---|---|---|---|
| 二进制 | 数值表达式 | 二进制 | 数值表达式 | 二进制 | 数值表达式 | |
| 最大正数 | 0.111…11 | 0.111…11 | 0.111…11 | |||
| 最小正数 | 0.000…01 | 0.000…01 | 0.000…01 | |||
| 0 | 0.000…00 | 0 | 0.000…00 | 0 | 0.000…00 | 0 |
| 1.000…00 | 0 | 1.111…11 | 0 | |||
| 最大负数 | 1.000…01 | 1.111…10 | 1.111…11 | |||
| 最小负数 | 1.111…11 | 1.000…00 | 1.000…00 | -1 |
定点数所能表示的 数据范围 与下列因素有关:
- 机器字长 :字长越长,其表示的数据范围就越大
- 所采用的 机器码 :补码和移码所能表示的数据范围,比原码和反码所能表示的数据范围 要多一个最小负数
实际上,计算机中处理的数 不一定都是纯小数或者纯整数 例如 , 因此这样的数 不能直接 用定点数表示
浮点数表示
二进制浮点数可采用 类似十进制科学记数法 的表示方法
其中底数(如2)是 基数r 在机器中是隐含约定的,不需要专门存储表示
指数(如10, 11)为二进制数,指数也就是 阶码E , 用 定点整数 表示
小数点后面的部分是 尾数M , 用 定点小数 表示
任意一个二进制数N可表示成如下形式 :
浮点数在机器中的表示形式
┌───────────────────────────────┬────────────────────────────────┐ |
阶码 :
-
阶码的位数决定了数据表示的范围,位数越多,能表示的数据范围就越大。
-
阶码的值决定了小数点的位置。
-
阶码可采用原码、补码、反码、移码进行表示。
尾数 :
- 尾数的位数决定了数据的表示精度。阶码长度相同时,分配给尾数的位数越多,数据表示的精度就越高。
- 尾数可采用原码、补码、反码进行表示。
| N | 阶码E | 尾数M | |
|---|---|---|---|
| 正数N最大值 | 最大值 | 正数最大值 | |
| 正数N最小值(浮点数的最小精度) | 最小值 | 正数最小值 | |
| 负数N最小值 | 最大值 | 负数最小值 | |
| 负数N最大值 | 最小值 | 负数最大值 |
【练习】
(1)设浮点数字长为8位,其中阶码3位(含1位阶符),尾数5位(含1位数符),阶码和尾数均以原码表示,基数r为8,则浮点数的最大最小值分别是多少?
(2)设定点数原码为8位,则定点数的最大最小值分别是多少?
(3)比较(1)(2)能得出什么结论?
(1)浮点数取最大值,即阶码取最大值,尾数取正数最大值
最大值=浮点数取最小值,即阶码取最大值,尾数取负数最小值
最小值=
(2)定点数最大值 =
定点数最小值 =
(3)浮点数有效扩大了数据表示范围
浮点数表示范围
尽管浮点数有效扩大了数据表示范围,但 受机器字长限制,浮点数仍然存在溢出现象
- 当浮点数的阶码大于最大阶码时,称为 上溢 ,此时机器 停止运算 ,浮点运算器件会显示溢出标志。
- 当浮点数的阶码小于最小阶码时,称为 下溢 ,虽然此时数据 不能被精确表示 ,但由于发生下溢时数据的绝对值很小,通常将尾数各位强置为0, 按机器0处理 ,此时机器可以 继续运行 。
当一个浮点数在正、负区域中但并不在某个数轴刻度上时,也会出现 精度 溢出的问题,此时只能用 近似数 表示
| 最小负数 | 最大负数 | 最小正数 | 最大正数 |
|---|---|---|---|
最小负数和最大负数之间是 负数区域 ,最小正数和最大负数之间是 正数区域
| 上溢 | 负数区域 | 下溢 | 0 | 下溢 | 正数区域 | 上溢 | |
一旦浮点数的位数确定后,合理分配 阶码E 和 尾数M 的位数,直接影响浮点数的 表示范围 和 精度
- 短实数(32位): 阶码E取8位(含1位阶符)尾数M取24位(含1位数符)
- 长实数(64位): 阶码E取11位(含1位阶符)尾数M取53位(含1位数符)
- 临时实数(80位): 阶码E取15位(含1位阶符)尾数M取65位(含1位数符)
【习题2】假设浮点数A和B的字长相同,A的阶码位数大于B的阶码位数,A的尾数位数小于B的位数位数,其他规定都相同,则A和B可表示的数的范围和精度是( C )。
A. B可表示的数的范围大且精度高
B. A和B可表示的数的范围和精度相同
C. A可表示的数的范围大但精度低
D. A可表示的数的范围大且精度高
【习题3】
某浮点数字长为12位,其中阶码4位(含1位阶符号),基数为2,尾数8位(含1位数符),若阶码和尾数都用补码表示,则该浮点数所能表示的最大正数是( D )。
A. B. C. D.
最大正数:
阶码数值位是3位,尾数数值位是7位
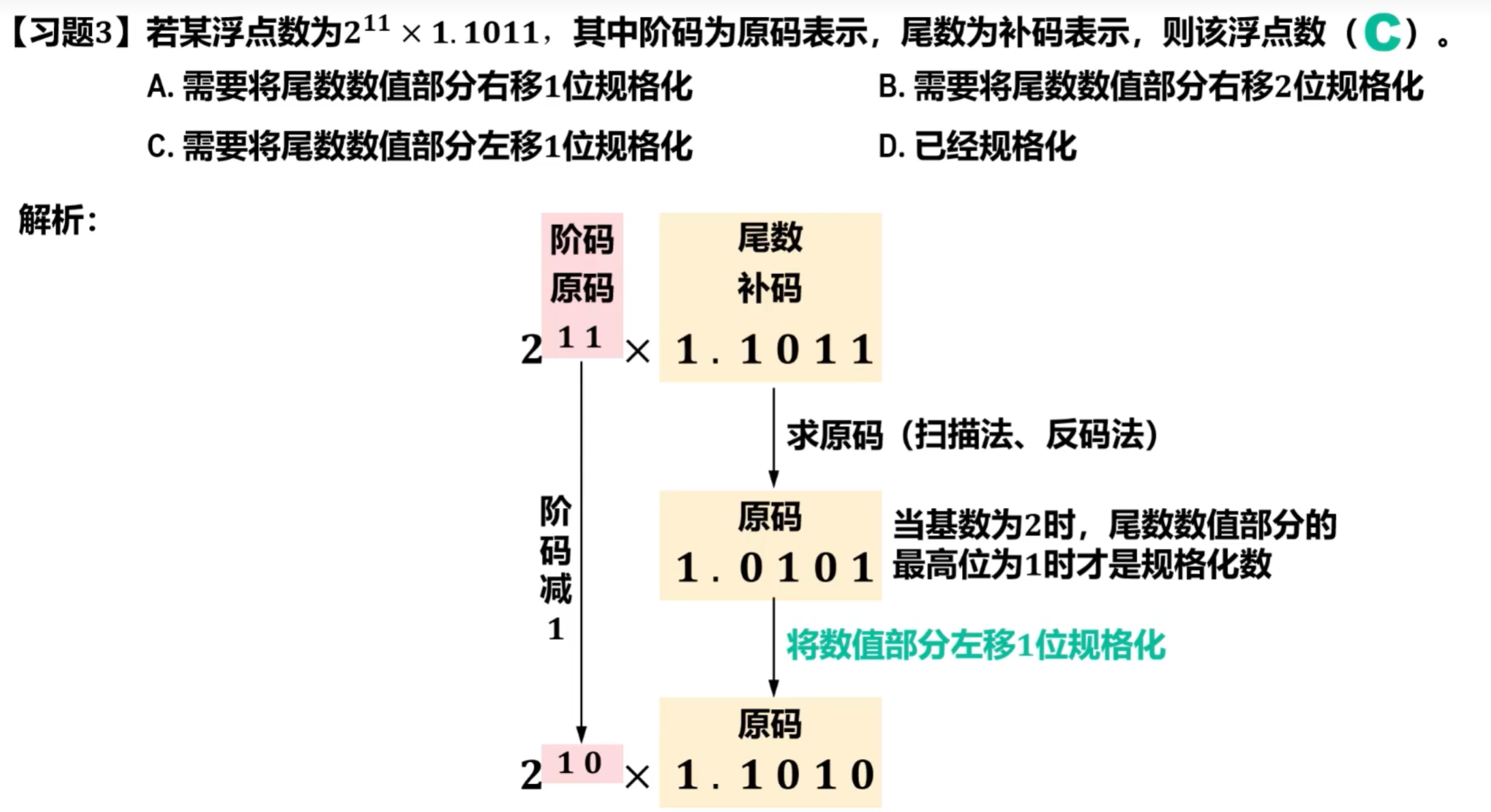
2.4.2 浮点数的规格化
通常要求浮点数在数据表示时 对尾数进行规格化处理 ,即 使得尾数的最高数值位必须是一个有效值 。
浮点数规格化有以下好处:
- 使浮点数的表示 形式唯一
- 使浮点数的表示 精度最高
对于非规格化尾数,需要对其进行 规格化操作 ,即根据具体形式通过将非规格化 尾数的数值部分 进行 左移或右移 ,并 相应减少或增加阶码值 的操作进行规格化,对应的规格化方法分别称为向左规格化(简称 左规 )和向右规格化(简称 右规 )。
对于 基数r不同的浮点数 ,因其 规格化数的形式不同 ,规格化 过程也不同 。
-
当 r = 2 时,尾数 数值部分最高位为1 的数为规格化数。
-
左规:尾数数值部分 每左移1位,阶码减1 。
-
右规:尾数数值部分 每右移1位,阶码加1 。
-
【举例】二进制浮点数
非规格化表示: 阶码数减1,尾数小数点左移1位
规格化表示:
-
-
当 r = 4 时,尾数 数值部分最高2位不全为0 的数为规格化数
- 左规:尾数数值部分每左移2位,阶码减1。
- 右规:尾数数值部分每右移2位,阶码加1。
-
当 r = 8 时,尾数 数值部分最高3位不全为0 的数为规格化数。
- 左规:尾数数值部分每左移3位,阶码减1。
- 右规:尾数数值部分每右移3位,阶码加1。
基数r不同,对数的 表示范围和精度等都有影响 ,一般来说:
- 基数r越大 ,可表示的 浮点数范围越大 ,而且所表示的数的 个数越多 ,但浮点数的 精度反而下降
【举例】
第二行为基数r=16的浮点数的尾数规格化
第三行为基数r=2的浮点数的尾数规格化
可见基数r=2时,比r=16时多3位精度
| … | |||||||
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | … | |||
| 1 | … |
浮点数规格化后的表示范围
相较于2.4.1,最小负数和最大正数不变
最大负数变为: 最小正数变为:
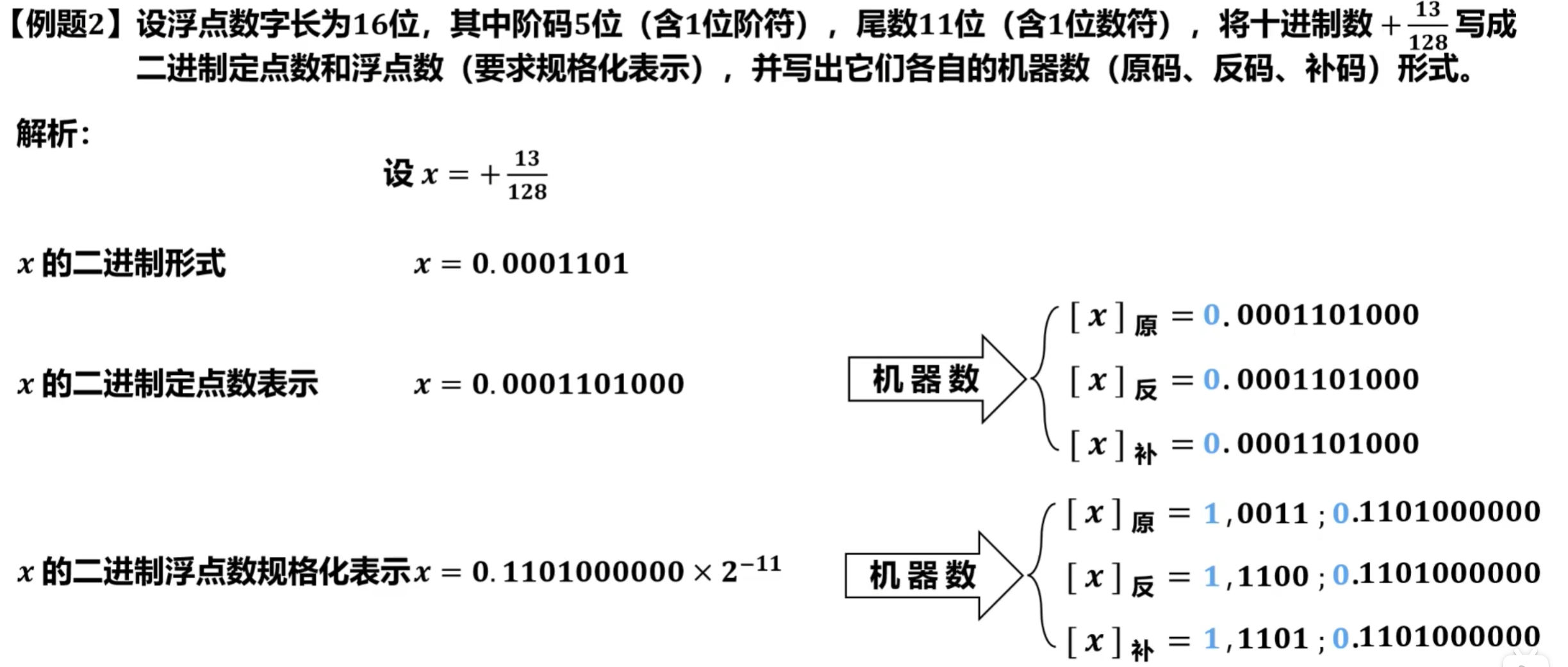
【例题1】
设浮点数字长为16位,其中阶码5位(含1位阶符),尾数11位(含1位数符),将十进制数-56写成二进制定点数和浮点数(要求规格化表示),并分别写出它们各自的机器数(原码、反码、补码)形式。
设
x 的二进制形式
x 的二进制定点数表示 (尾数有10位数值位,须补零)
x 的二进制浮点数规格化表示 (小数点应右移6位,因此乘2的6次方)
二进制定点数转换
二进制浮点数转换

2.4.3 IEEE 754 浮点数标准
IEEE 754标准主要包括两种基本的浮点数格式:
- 32位单精度浮点数 (对应C语言的float型)
|<----------32bit---------->| |
- 64位双精度浮点数 (对应C语言中的double型)
|<-----------64bit---------->| |
其中:
- 符号 :取值0表示正数;取值1表示负数。
- 阶码 :定点整数,用 移码 表示。
- 尾数 :定点小数,用 原码 表示。
IEEE 754 单精度浮点数的阶码
用移码来表示阶码的特点:
- 真值0在移码中只有一种表示。
- 移码保持了真值原有的大小顺序,可以直接比较大小。(不考虑移码的符号位 看作无符号二进制数)
- 最小真值的移码为全0,最大真值的移码为全1,符合人们的习惯。
在IEEE 754 浮点数标准中,32位单精度浮点数的 8位阶码尽管采用移码表示 ,但 **采用偏移常数是 ** ,而 **不是标准的 ** 。
| 真值 | IEEE | |
|---|---|---|
| -128 | 0,0000000 | 1,1111111 |
| -127 | 0,0000001 | 0,0000000 |
| … | … | … |
| -2 | 0,1111110 | 0,1111101 |
| -1 | 0,1111111 | 0,1111110 |
| 0 | 1,0000000 | 0,1111111 |
| 1 | 1,0000001 | 1,0000000 |
| 2 | 1,0000010 | 1,0000001 |
| … | … | … |
| 125 | 1,1111101 | 1,1111100 |
| 126 | 1,1111110 | 1,1111101 |
| 127 | 1,1111111 | 1,1111110 |
为什么偏移常数不采用标准的128,而采用127?
- 将阶码全为1、全0的对应到最小的两个数-128和-127,有特殊用途
- 采用偏移常数128表示的最小规格化数的 倒数会发生溢出 ,而采用偏移常数127表示的任何一个规格化数的倒数则不会溢出。
IEEE 754 单精度浮点数的尾数
尾数的特点:
- 符号位前移到最左侧。相邻左侧隐藏一个1,表示数值而不表示符号。
- 尾数实际有24位,但不保存隐藏的那个1,只保存23位,节省的比特位可用于提高尾数的精度。
- 完整的尾数形式为1.M
IEEE 754 单精度浮点数标准
| 数值的分类 | 符号 S | 阶码 E | 尾数 M | 真值(LaTeX) |
|---|---|---|---|---|
| 正零 | 0 | 0(全0) | 0 | +0 |
| 负零 | 1 | 0(全0) | 0 | −0 |
| 非规格化正数 | 0 | 0(全0) | ||
| 非规格化负数 | 1 | 0(全0) | ||
| 正无穷大 | 0 | 255(全1) | 0 | |
| 负无穷大 | 1 | 255(全1) | 0 | |
| 无定义数(非数) | 0 或 1 | 255(全1) | (not a number) | |
| 规格化正数 | 0 | M | ||
| 规格化负数 | 1 | M |
- 一般情况下,+0 和 -0 是等效的。
- 非规格化数可用于处理阶码下溢,使得出现比最小规格化数还小的数时程序也能继续进行下去。
- 引入无穷大数可使计算过程中出现异常的情况下程序能继续执行,并且可为程序提供错误检测功能。例如非0浮点数除0运算的结果就是无穷大,因此非0浮点数除0不会像整型数除0一样产生严重错误。
- 非数 则用于表示 、、、、负数的平方根等。部分非数 运算结果可能会产生异常。
IEEE 754 单精度浮点数与对应真值之间的转换
【例题1】将十进制数 转换成 IEEE 754 单精度浮点数的十六进制机器码
尾数不足23位则在后面补零
按四个一组进行二进制到十六进制的转换,即
【例题2】若 是某个IEEE 754单精度浮点数的十六进制机器码,求其对应的十进制值
将十六进制数转换为二进制数
符号S=1,阶码E=10000011,尾数M=00000110000000000000000
阶码的真值 ,尾数的1.M形式=1.0000011
浮点数的真值
IEEE 754 单精度浮点数的表示范围
| 数值分类 | |
|---|---|
| 规格化 | |
| 正数最大值 | |
| 正数最小值 | |
| 负数最大值 | |
| 负数最小值 | |
| 非规格化 | |
| 正数最大值 | |
| 正数最小值 | |
| 负数最大值 | |
| 负数最小值 |
【2012考研 题14】float类型能表示的最大正整数是( D )
A. B. C. D.
根据上表的推导公式 进行化简可知
【2021考研 题14】下列数值中,不能用IEEE 754浮点格式精确表示的是( A)
A. 1.2 B. 1.25 C. 2.0 D. 2.5
将这些十进制数转换为二进制数会发现 是无限循环的,而IEEE 754浮点数格式位数有限,无法精确表示无限循环小数
3.1.1 逻辑移位
-
逻辑移位的对象: 无符号数
-
逻辑移位的规则:
-
逻辑左移 :高位移除,低位补零
-
逻辑右移 :低位移除,高位补零
-
【举例】假设某寄存器的内容如下所示,请给出逻辑左移3位和逻辑右移1位的结果
| 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 |
逻辑左移3位后,即高位移除了1,0,1,低位补3个0
| 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
逻辑右移1位后,即低位移除了0,高位补1个0
| 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 |
3.1.2 算术移位
-
算术移位的对象: 有符号数 (针对定点数,包括定点整数和定点小数)
-
不论正数还是负数, 符号位保持不变,仅对数值位进行移位 (左移或右移)。
-
对真值的原码、反码和补码进行算术移位后,它们各自所对应的新的真值应该保持一致。
-
当真值为 正数 时,真值的 原码、反码和补码都相同 ,因此,对它们进行算术移位后,它们各自所对应的新的真值自然是保持一致的。对于 移位后出现的空位,规定添补0 。左移时,若最高位丢1,则 结果出错 ;右移时,若最低位丢1,则 精度缺失 。
-
当真值为 负数 时,真值的 原码、反码和补码都不同 ,因此,对它们进行算术移位后,为了确保它们各自 所对应的新的真值保持一致 ,对于 移位后出现的空位,添补规则各不相同 ,我们稍后推导给出它们各自具体的添补规则。
-
真值 机器码 空位填补 丢位情况 算术移位效果 正数 原码=补码=反码 0 最高位丢1,结果出错 最低位丢1,精度缺失 在未出现因丢位产生结果出错或精度缺失的情况下: ● 左移:乘以 ● 右移:除以 其中, 为移位次数。 负数 原码 1 最高位丢0,结果出错 最低位丢0,精度缺失 反码 1 最高位丢0,结果出错 最低位丢0,精度缺失 补码 左移补0 最高位丢0,结果出错 补码 右移补1 最低位丢1,精度缺失
-
-
【练习1】假设机器数字长为8位(含1位符号位),若真值 ,请写出 的补码算术左移1位、2位后的表示形式以及对应的真值 , ,并对移位结果进行分析。
为符号位
下面三行分别为补码、算术左移1位、算术左移2位
| 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
可见,左移1位高位丢0,相当于乘以 ,而左移2位后,高位丢01,含1,所以 结果出错
【练习2】假设机器数字长为8位(含1位符号位),若真值 ,请写出 的反码算术右移1位、2位、3位后的表示形式以及对应的真值 、、,并对移位结果进行分析。
下面四行分别为反码、算术右移1位、算术右移2位、算术右移3位
| 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
可见,右移1位和右移2位时,都是低位丢0,相当于除以 和
而右移3位,结果发生变化,并非除以了 ,精度缺失
【练习5】假设机器数字长为8位(含1位符号位),若真值 ,请写出 的补码算术左移1位、2位、3位后的表示形式以及对应的真值 、、,并对移位结果进行分析。
下面四行分别为补码、算术左移1位、左移2位、左移3位
| 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
根据补码的计算方式(或者说形式)可知,高位(左侧部分)和反码一样,低位(右侧部分)和原码一样,所以说左移的规则同反码,右移的规则同原码。
可见,左移1位和2位,分别是高位丢1,和高位丢11,也就是乘以 和 , 左移3位时,高位丢110,含0,结果出错
补码的“符号位参与”移位法
有符号定点数的补码的另一种算术移位方法,即“符号位也参与移位”,具体规则如下:
- 左移:高位移除,低位添补0;移动前后 若符号位发生变化,则发生溢出 。
- 右移:低位移除, 高位添补符号 (0或1)
上述这种针对有符号定点数的补码的算术移位方法,具有以下优点:
-
左移时,有检测出发生溢出的方法:符号位发生变化可判定溢出。
-
符号位与数值位一起移位, 方便ALU处理 ,也方便人们记忆。
【举例】假设机器数字长为8位(含1位符号位),若真值 ,请写出 的补码算术右移1位、2位后的表示形式以及对应的真值 、,并对移位结果进行分析。
下面三行分别为补码、算术右移1位、右移2位
| 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
高位补符号0
【练习9】假设机器数字长为8位(含1位符号位),若真值 ,请写出 的补码算术左移1位、2位、3位后的表示形式以及对应的真值 、、,并对移位结果进行分析。
| 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
题目同练习5,方法不同。左移3位时,发现符号位由1变0,即为发生溢出
算术移位的应用举例
假设 ,仅用 加法和算术移位 操作计算
对 算术左移1位可得其乘以2的结果,然后将 和 相加即可
【2018考研 题16】整数 的机器数为 ,分别对 进行逻辑右移1位和算术右移1位操作,得到的机器数各是( B )。
A. 1110 1100、1110 1100
B. 0110 1100、1110 1100
C. 1110 1100、0110 1100
D. 0110 1100、0110 1100
- 逻辑右移1位:将其当作无符号数,高位补0,结果为
- 算术右移1位:将其当作有符号数,则机器数 就是 的补码,高位补符号位(原最高位为1),结果为
3.1.3 循环移位
- 循环移位的对象:无符号数
- 将无符号数二进制形式中的各个位向左或向右移动, 被移出的位会重新出现在另一端,形成循环 。
- 在很多处理器架构中,循环移位指令会影响状态寄存器中的进位标志CF(Carry Flag)位,CF标志位用于标识在执行算术或逻辑移操作时是否发生了进位。
- 根据 CF标志位是否加入循环移位 过程,循环移位可分为以下四种:
- 不带CF标志位的循环右移
- 不带CF标志位的循环左移
(合称为小循环) - 带CF标志位的循环右移
- 带CF标志位的循环左移
(合称为大循环)
不带CF标志位的循环右移
最低位移出的值会存入最高位,CF标志位本身不存在于循环右移中,CF位的值为最低位移出的值
第三行为循环右移一次的结果,CF标志位此时的值为
不带CF标志位的循环左移
基本同上。最高位移出的值会存入最低位,CF位的值位最高位移出的值
带CF标志位的循环右移
寄存器中的值整体向右移动(包括CF位),最低位移出的值会存入CF位,CF位移出的值会存入最高位( )
| CF | ||||||||
|---|---|---|---|---|---|---|---|---|
带CF标志位的循环左移
基本同上。寄存器中的值整体向左移动(包括CF位),最高位移出的值会存入CF位,CF位移出的值会存入最低位( )
循环移位的应用
- 循环移位的应用主要有:加密算法、哈希函数、优化算法
- 加密算法:通过循环移位可以实现数据的混淆和置换,增强加密算法的安全性。
- 哈希函数:通过循环移位可以用来改变输入数据的排列顺序,以产生不同的哈希值,有利于增强哈希函数的混淆性和扩散性。
- 优化算法:在某些算法中,循环移位可以用于优化性能和节省资源。例如,在图形处理和数字信号处理中,循环移位可以用于加速算法的执行。
3.2.1 补码加减法运算公式
-
经过第2章的学习可知,定点数(定点整数和定点小数)在计算机内部采用补码表示,原因如下:
- 补码的符号位可以与数值位一起参加加运算。
- 采用补码可将减法运算转换成加法运算。
- 运算规则简单,易于实现。
-
补码加法和减法运算的公式如下:
-
-
()
-
【例题1】设 , 求 。
【例题2】设 , 求 。
【例题3】设 , 求 。
3.2.2 补码加减法的溢出检测
- 计算机的字长是有限的,因此所能表示的数据范围也是有限的。
- 当运算结果超出所能表示的数据范围时,就会出现溢出(Overflow)。
- 溢出会导致错误的运算结果。
- 计算机系统设计人员必须要解决溢出的检测问题,以便在发生溢出时计算机能做出相应的处理

如图所示,两负数相加,舍去进位的模数后,结果变为正数,出现错误
两正数相加,舍去进位的模数后,结果变为负数,出现错误
(出现错误的原因并非计算过程中和模数 有关的部分)
溢出检测
定点数补码加减运算判断溢出的方法主要有以下3种:
-
方法1:根据 操作数的符号位 与 运算结果的符号位 是否一致进行判断
-
两个操作数 相加 时,当它们的 符号位相同 时,才 可能发生溢出
-
若运算结果的符号位与原操作数的 符号位不同 ,则为 溢出
-
由于采用补码可将减法运算转换成加法运算,因此不论作加法还是减法,只要 实际参加运算的两个操作数符号相同 , 但运算结果的符号位与原操作数不同 ,即为 溢出 。
-

-
操作数 的符号位记为 操作数 的符号位记为 运算结果 的符号位记为
溢出标志位 记为 , 表示发生溢出。 -
-
-
方法2:根据运算过程中 最高数值位的进位 与 符号位的进位 是否一致进行判断
-
-
方法3:利用 变形补码 (具有2位符号位的补码)的符号位进位进行判断
- 双符号位为 00 时,表示正数;
- 双符号位为 01 时,表示正溢出;
- 双符号位为 11 时,表示负数;
- 双符号位为 10 时,表示负溢出;
【2009考研 题12】一个C语言程序在一台32位机器上运行。程序中定义了三个变量x,y和z,x和z为int型,y为short型。当x = 127,y = -9时,执行赋值语句z = x + y后,x,y和z的值分别是( D )。
A.
B.
C.
D.
y的补码可得为 FFF7H,z的真值由计算可得为118>0 所以符号位应为0
【2013考研 题14】某个字长为8位的计算机中,已知整型变量x和y的机器数分别为x补 = 11110100,y补 = 10110000。若整型变量 ,则z的机器数为( A )。
A.
B.
C.
D. 溢出
将 算术左移1位可得 :
- 高位移除,低位补0;
- 移动前后若符号发生变化,则发生溢出。
将 算术右移1位可得 :
- 低位移除,高位补符号位。
相加,符号位进位的值为模数,应舍弃,符号位进位的值等于操作数,不溢出
3.5.1 浮点加减法运算
- 在尾数右规时,尾数末位的几位会因超出计算机字长而被丢弃,从而产生误差。此时,计算机可以按选定的方式进行舍入操作。
- 在尾数规格化和尾数舍入时,可能会对结果的阶码执行加、减运算。因此,必须考虑结果的阶码出现溢出的问题。
- 由于浮点数中阶码的位数决定了浮点数的表示范围,因此,对于浮点运算,当阶码出现溢出时,表示运算结果出现溢出。
注:下例并不符合IEEE 754标准
【例1】设,,x和y的阶码和尾数都用 双符号补码 表示,阶码为3位、尾数为6位(均不含符号位),请按照浮点数加减法运算步骤计算。
解析:
对阶
对阶原则: 小阶向大阶看齐 ,尾数右移相应位数(两个阶的差的绝对值)
这表明:x的阶码比y的阶码小3
因此,x的阶码应向y的阶码看齐(即相同);相应地,需要将x的尾数向右移动3位
对阶后:
上式括号中的101是移出位,但暂时保留,称为 保留附加位 。保留附加位参与中间运算以提高运算精度 ,尾数运算结束,结果规格化后再进行舍入。
尾数运算
结果规格化
左规 :
- 尾数运算结果为 或 :
- 尾数每左移1位,阶码减1 ,直到尾数成为规格化数为止。
- 还需要判断阶码是否 下溢 。若发生下溢(符号位为10),可认为 结果为0 。
右规 :
- 尾数运算结果为10.bb … b或01.bb … b,即尾数运算结果溢出:
- 尾数只需要右移1位,阶码加1。
- 还需要判断阶码是否上溢。若发生上溢(符号位为01),可认为结果为∞。
本题则符合左规的条件,算术左移2位,得到
且有2位保留附加位直接移入了数值位。因此,采用保留附加位可以提高运算精度。
相应的,将阶码减2,得到
当阶码的符号位为01(上溢)和10(下溢)时表示溢出。因此本例未溢出。
舍入处理
在进行对阶时会用到算术右移,而进行结果规格化时,可能会用到算术右移。这会导致尾数末位的几位因超出机器字长而被丢掉,从而产生误差。此时,机器可按选定方式进行舍入处理:
-
截断法 :直接丢弃超出机器字长的尾数低位(导致 误差积累 )
-
末位恒置1法 :将机器字长内的尾数的最低位恒置为1(损失1位精度,但误差积累较小)
-
0舍1入法 :当需要丢弃的尾数低位中的最高位为1时,将机器字长内的尾数的最低位加1
采用该方法,若破坏规格化结果,则还需要再次进行规格化处理
对于本题,运用以上方法来处理要被舍弃的最后一位1,结果分别如下:
【练习】下列有关浮点数加减运算的叙述中,正确的是( D )。
I. 对阶操作不会引起阶码上溢或下溢
II. 右规时可能引起阶码上溢
III. 左规时可能引起阶码下溢
IV. 尾数溢出时浮点数本身不一定溢出
A. 仅II、III
B. 仅I、II、IV
C. 仅I、III、IV
D. I、II、III、IV
3.5.2 IEEE 754 浮点数运算
图中包含以下文字:
IEEE 754浮点数的阶码采用移码表示,尾数采用原码表示,并且尾数的最高位隐藏。
因此,IEEE 754浮点数的加减运算与(上节课介绍的)基于补码表示的浮点数的加减运算有如下不同:
- 在对阶和结果规格化过程中,涉及到 阶码的加减运算时采用 移码的加减运算 规则。
- 尾数运算采用原码运算规则,且隐藏位要参与尾数运算 。
- 隐藏位参与尾数规格化判断和规格化过程 。
- 若尾数形式为1……,则为 规格化 尾数。
- 若尾数形式为0……,则需要进行 左规 (将尾数左移1位,相应地将阶码减1), 直到尾数规格化为止 。
- 若尾数形式为1b……,则需要进行 1次右规 (将尾数右移1位,相应地将阶码加1)。
- 舍入处理 :
- 就近舍入:舍入为可表示的最近的数,如果数据正好处于两个可表示的数的中间,则向偶数舍入。
- 朝 方向舍入:总是取右侧可表示的最近的数。
- 朝 方向舍入:总是取左侧可表示的最近的数。
- 截断处理:直接丢弃多余位,朝0方向舍入。
- 溢出判断 :
- 浮点运算的溢出可通过阶码的溢出来判断。对于IEEE 754单精度浮点数而言,向右规格化使阶码为全1(即11111111,真值为-128)时发生 规格化上溢 ;向左规格化使阶码为全0时发生 规格化下溢 。
【举例】设IEEE 754单精度浮点数x和y的机器码分别为 , , 求
首先将其转换为二进制形式:
可知, 阶码相同,无需对阶
考虑到IEEE 754浮点数的 隐藏位 ,可得
小数点后面的第一个1就是隐藏位
M需要进行左规,小数点左移1位,阶码减1, ,
IEEE 754规定,阶码全为0时为非规格化浮点数。因此,该运算结果产生了 规格化下溢 ,所以本例结果应为 非规格化 形式
4.1 存储器概述
- 现代计算机以存储器为中心,它是计算机中存放指令和数据的主要部件。
- 存储器的容量越大,能存储的信息越多。
- 提高存储系统的访问速度,是提高计算机处理信息速度的重要措施。
- 因此,开发具有大容量、高速度和低成本的存储系统是计算机技术发展的关键目标之一。
4.1.1 存储器分类
存储介质
按 存储介质 可分为 磁存储器、光存储器、半导体存储器 。
磁存储器 :
- 以磁性材料作为存储介质。
- 利用磁化单元的不同磁化方向来存储数据0和1。
- 主要包括磁芯、磁盘、磁带存储器。
- 磁盘、磁带中都包含有机械装置,因此体积大、存取速度慢,但其单位容量成本最低。
光存储器 :
- 利用介质的光学特性读出数据。
- 例如CD-ROM、DVD-ROM都以刻痕的形式将数据存储在盘面上,用激光束照射盘面,靠盘面的不同反射率来读出信息。
- 光盘存储器成本低廉,适用于电子出版物的发行。
半导体存储器 :
- 用半导体器件组成的存储器。
- 存取速度快、体积小、性能可靠,但单位容量成本相对较高。
存取方式
按 存取方式 可分为 顺序存储器、随机存储器、直接存储器 。
顺序存储器 :
- 存储单元中的内容只能按地址顺序访问。
- 存取速度与存储单元的位置有关。
- 磁带存储器就是典型的顺序存储器。
随机存储器 :
- 可按指定的任何一个存储单元的地址对其内容进行存取。
- 存取速度与存储单元的位置无关。
- 早期的磁芯存储器和当前广泛使用的半导体存储器都是随机存储器。
直接存储器 :
- 不必经过顺序搜索就能在存储器中直接存取信息。
- 兼有随机存储器和顺序存储器的访问特性。
- 典型的如磁盘存储器。由于磁盘存在机械寻道和旋转延迟,因此数据访问时间和磁头与目标扇区的距离有关。
可改写性
按 可改写性 可分为 读写存储器、只读存储器 。
读写存储器 :
- 既能读出也能写入信息
只读存储器 :
- 存储的内容不允许被改变,只能读出。
- 常见的有光盘存储器。
- 还有半导体只读存储器,信息只能读出,不能随意写入。主要用来存放一些不需要修改的程序(例如BIOS)和常量。
可保存性
按 可保存性 可分为 易失性存储器、非易失性存储器 。
易失性存储器 :
- 断电后所保存的信息会丢失
非易失性存储器 :
- 断电后所保存的信息不会丢失
功能和存取速度
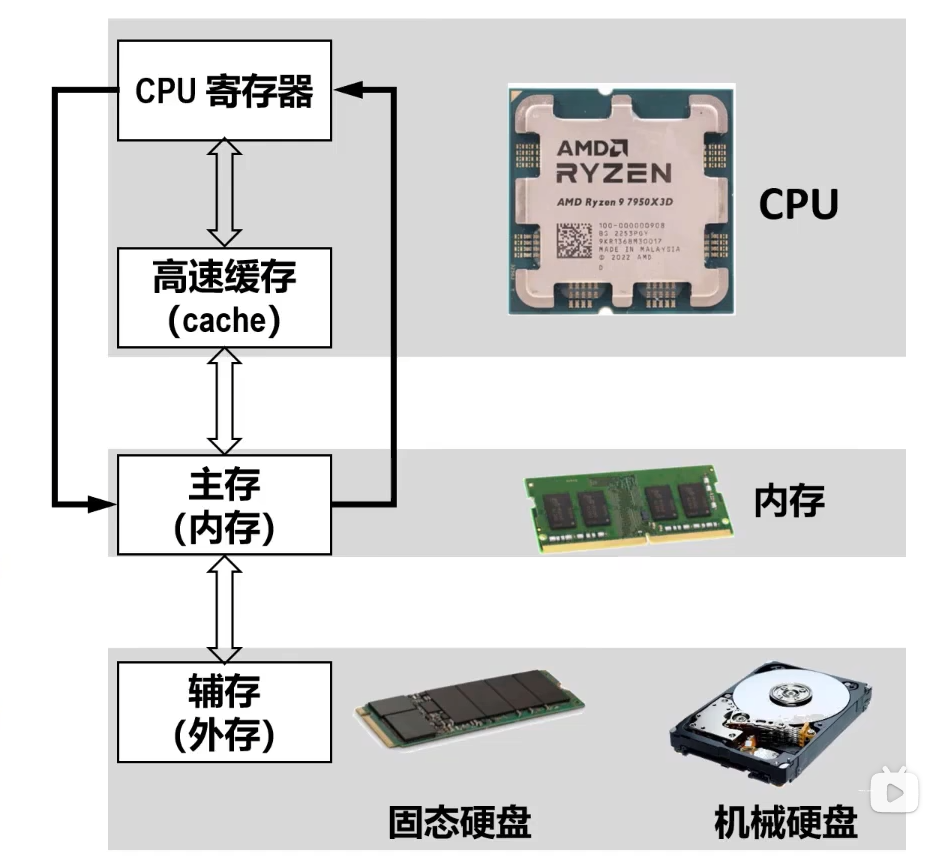
按 功能和存取速度 可分为 寄存器存储器、高速缓冲存储器、主存储器、辅助存储器 。
寄存器存储器 (CPU寄存器):
- CPU内部的多个寄存器(例如MAR、MDR、ACC、MQ等)。
- 用于存放地址、数据以及运算的中间结果。
- 速度与CPU匹配,容量极小。
高速缓冲存储器 (cache):
- 寄存器与主存之间的一个高速小容量存储器。
- 用于缓冲CPU与主存之间的性能差异,提高存储系统的访问速度。
- 存放内容一般是即将或经常要使用的指令和数据。
主存储器 (内存):
- 用于存放指令和数据。
- CPU可以通过主存地址随机地读写主存。
- 存取速度低于高速缓存,但一般高于辅存。
- 容量远大于高速缓存,但一般远小于辅存。
辅助存储器 (外存):
- 存放当前暂不参与运行的程序和数据,以及一些需要长期保存的信息。
- 容量很大,但存取速度相对较低。
| 存储器 | 按存储介质 | 按存取方式 | 按可改写性 | 按可保存性 | 按功能和存取速度 |
|---|---|---|---|---|---|
| 磁带 | 磁存储器 | 顺序存储器 | 读写存储器 | 非易失性存储器 | 辅存(外存) |
| 机械硬盘 | 磁存储器 | 直接存储器 | 读写存储器 | 非易失性存储器 | 辅存(外存) |
| 光盘 | 光存储器 | 直接存储器 | 只读存储器 | 非易失性存储器 | 辅存(外存) |
| BIOS芯片 | 半导体存储器 | 随机存储器 | 只读存储器 | 非易失性存储器 | 辅存(外存) |
| 固态硬盘 | 半导体存储器 | 随机存储器 | 读写存储器 | 非易失性存储器 | 辅存(外存) |
| CPU寄存器 | 半导体存储器 | 随机存储器 | 读写存储器 | 易失性存储器 | 寄存器存储器 |
| cache | 半导体存储器 | 随机存储器 | 读写存储器 | 易失性存储器 | 高速缓冲存储器 |
| 内存 | 半导体存储器 | 随机存储器 | 读写存储器 | 易失性存储器 | 主存(内存) |
4.1.2 存储器性能指标与存储系统层次结构
存储器性能指标 分为 存储容量、存取速度 这两个性能指标
存储容量
-
存储容量是指存储器可以 存储的二进制信息的总量 。
-
如主存储器中有MAR和MDR,MAR的位数决定了 存储单元 的数量,MDR的位数与 存储字长 相等
-
存储速度
存取时间 :
- 启动一次存储器操作到该操作完成所经历的时间。
- 读出时间
- 写入时间
- 读出时间和写入时间可能不同
存取周期 :
-
连续两次访问存储器操作(读操作或写操作)之间所需要的最短时间间隔。
-
对于主存,存取周期除包括存取时间外,还包括存储器状态的稳定恢复时间,因此存取周期略大于存取时间。
| 第 n 次存取 | 恢复时间 | 第 n+1 次存取 |
| 存取周期 |
存储器带宽 :
- 单位时间内存储器所能传输的信息量(单位:b/s或B/s)。
- 它是衡量数据传输速率的重要指标,与一次传输的数据位的多少和存取时间的长短有关。
- 一般而言,数据位宽越大、存取时间越短,则存储器带宽越高。
存储器层次结构
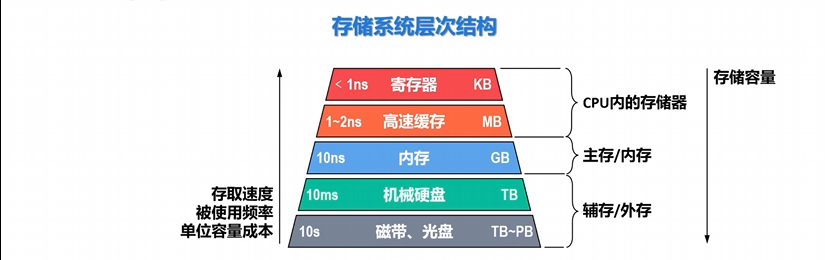
- 上层存储器可为下层存储器做缓冲 ,将最经常使用的数据的副本调度到上层,使得CPU只需要访问上层的快速小容量存储器即可获得大部分数据。可以 有效提高存储系统的访问速度,缓解CPU与主存(内存)、主存(内存)与辅存(外存)的性能差异 。
- 另外, 使用大容量辅存 (外存), 缓解了主存(内存)容量不足的问题 。
- 基于这种层次结构,就可构建出满足应用需求的 存储容量大、存取速度快、成本低 的存储系统。
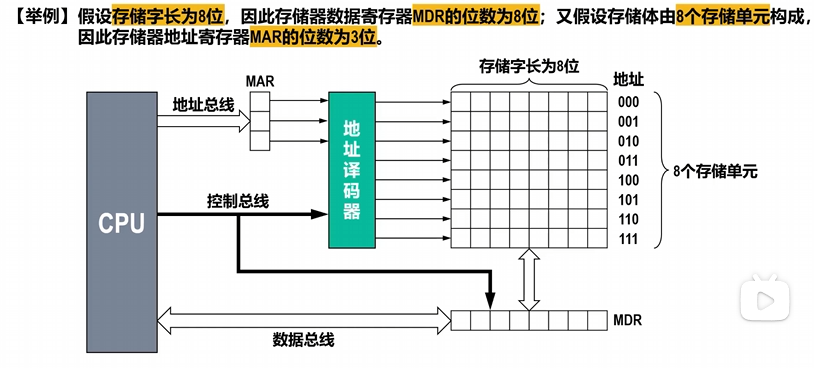
4.1.3 主存的基本结构
-
主存是机器指令直接操作的存储器,需要基于 主存地址 对其进行 随机访问 。
-
-
CPU 从主存中读取信息 的过程:
-
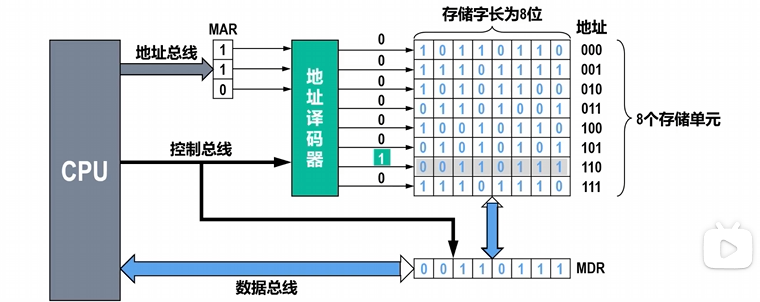
-
CPU通过地址总线将某值(如图中的110)送入MAR
-
CPU通过控制信号,控制地址译码器进行译码输出
-
CPU通过控制信号,控制主存将该存储单元中的信息读取到存储器数据寄存器MDR中暂存
-
CPU通过控制信号,将MDR中的信息通过数据总线 读取到CPU中
-
-
CPU 向主存中写入信息 的过程:
-
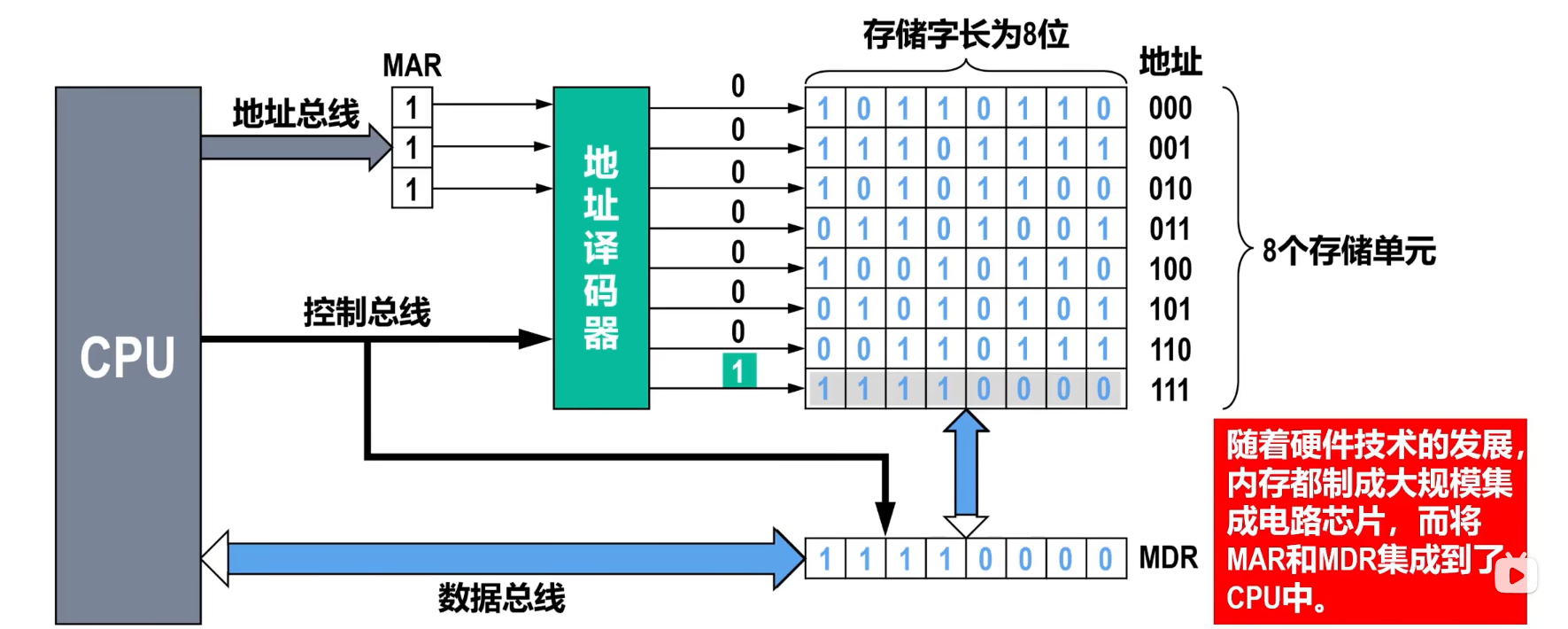
- CPU通过数据总线,将待写入主存中的信息,写入到主存的MDR中
- CPU通过地址总线,将待写入信息的存储单元的地址,送入存储器地址寄存器MAR中
- 假设待写入信息的存储单元的地址为某值(如图中的111)
- CPU通过控制信号,控制地址译码器进行译码输出
- CPU通过控制信号,将之前送入到MDR中的信息,写入到该存储单元
-
4.1.4 用于地址译码的译码结构
单译码结构
【举例】若主存的存储体包含64个存储单元,每个存储单元只能存储1个二进制位,请给出只使用一个译码器就能寻址这64个存储单元的方案(即译码器的地址输入线和译码输出线各需要几条)。
因为 所以 地址输入线 有6条, 译码输出线 数量和存储单元数量相等,也就是64条
若存储体包含64k个存储单元,则译码器的地址输入线和译码输出线各需要几条?
64k条 ; 16条()
- 随着存储容量(存储体中存储单元的数量)的增大,译码输出线也随之增多,这样,译码电路的开销就不容忽视,过多的译码输出线也会占用较多的晶圆面积,为生产制造带来困难。
- 因此, 单译码结构只适用于容量很小的存储芯片 (例如容量在几百个存储单元以内的存储芯片)。
双译码结构
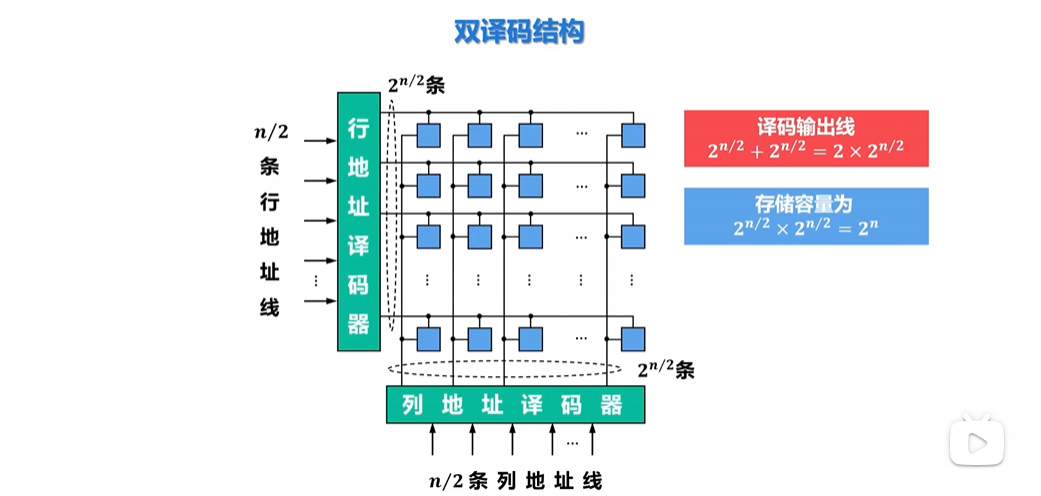
【举例】若相同存储容量,改用单译码结构,则译码输出线有多少条?
条
- 在大容量存储器中普遍采用双译码结构
4.1.5 主存中数据的存放
机器字长与存储字长的区别
- 机器字长:
- 定义:CPU一次能够处理的二进制数据的位数。
- 存储字长:
- 定义:主存中的一个存储单元所能存储的二进制位数。
- 注意事项:
- 存储字长与机器字长不一定相同。
- 例如:机器字长为32位的计算机,所采用的存储字长可以是16位、32位或64位。
地址访问模式
- 主存通常按字节进行编址,而存储字长(主存中的一个存储单元所能存储的二进制位数)是字节的2的整数次幂倍(例如1字节,2字节,4字节)。
- 以机器字长为 32位 的计算机为例,对主存的访问既可以按 字节访问 ,也可以按 16位半字访问 ,还可以按 32位字访问 。因此,可将主存地址分为:
- 字节地址
- 半字地址
- 字地址
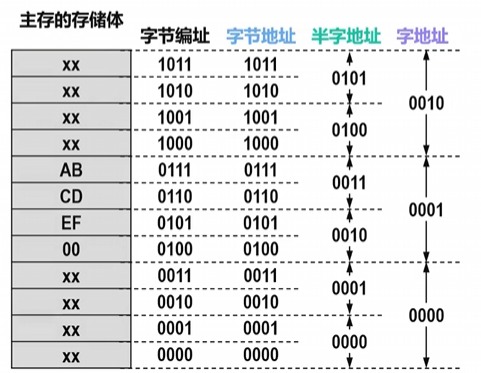
- 不同的地址访问模式 (字节访问、半字访问、字访问) 所使用的主存地址实际上都是字节地址 。
- CPU在执行指令的时候可以将字节地址的低2位用于访问控制:
- 采用字节访问模式,字节地址的低2位用于选择字存储单元中的哪一个字节。
- 采用半字访问模式,字节地址的倒数第2位用于选择字存储单元中的哪个半字。
小端和大端方式
(下图上部分为小端方式,下部分为大端方式)
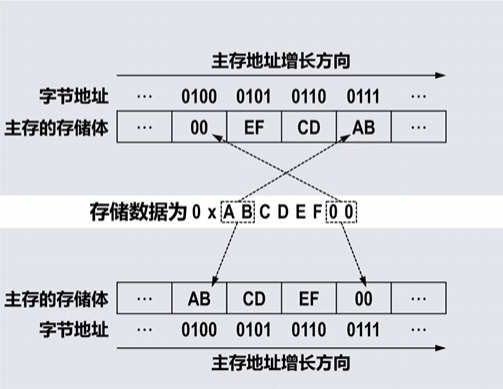
小端方式
- 将数据的低字节保存在主存的低地址中,而数据的高字节保存在主存的高地址中。
- 这样可以将主存地址的高低与数据的位权有效地结合起来,高地址存储的数据部分的权值高,低地址存储的数据部分的权值低,符合逻辑。
- Intel x86、IA64、RISC-V等处理器采用小端方式。
大端方式
- 将数据的高字节保存在主存的低地址中,而数据的低字节保存在主存的高地址中。
- 符合人类的正常思维。
- PowerPC处理器采用大端方式;ARM、MIPS等处理器同时支持大端方式和小端方式。
注意事项
- 上述两种方式并没有绝对的优劣之分,它们在不同的处理器架构和应用场景中都有各自的适用性和优势。
- 除处理器外,大小端方式还涉及外部设备设计、网络数据传输、音视频文件保存等。
- 小端与大端方式的区别不仅存在于处理器的寄存器、存储器中,在指令集、系统总线等各个层次中也可能存在差别。
数据的边界对齐
- 主存空间 通常按字节进行编址。
- 高级语言中 不同数据类型的变量 所包含的字节数量可能不同。
- 编译器在为这些变量分配主存空间时,理论上可以从主存空间的任何一个字节地址开始。
- 当一个多字节变量被编译器 分布在不同的字存储单元中 时,访问该变量就需要 多个存取周期 。
- 为了 提高数据访问效率 ,应该要考虑数据变量、数据结构在 主存空间中的边界对齐问题 。
【举例】假设存储字长为32位,为C语言不同数据类型的变量分配主存空间
数据的边界未对齐
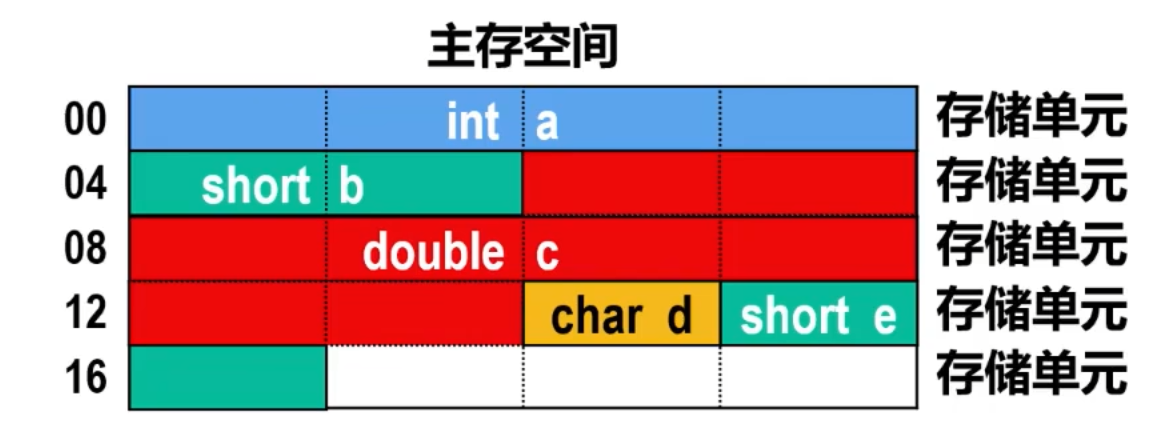
- 对存储空间的利用率最高
- 存在访问性能问题,例如:
- 变量c的8个字节分布在3个存储单元中(访问该变量需要3个存取周期)
- 变量e的2个字节分布在2个存储单元中(访问该变量需要2个存取周期)
数据的边界对齐

- 有效提升了访问性能,例如:
- 变量c的8个字节分布在2个存储单元中(访问该变量需要2个存取周期)
- 变量e的2个字节分布在1个存储单元中(访问该变量需要1个存取周期)
边界对齐的规则
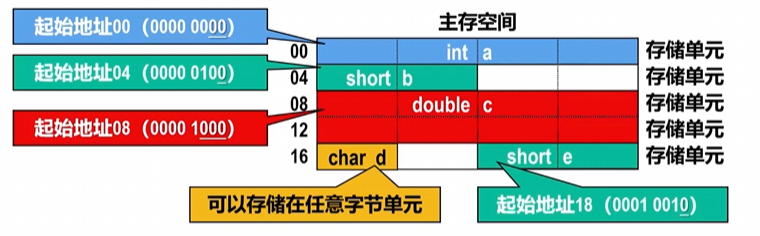
- 字节数据 不存在边界对齐问题(因为主存空间就是按字节编址的 如char型)
- 半字(2字节) 数据的起始字节地址的最低1位为0(即地址是2的整数倍 如short型)
- 单字(4字节) 数据的起始字节地址的最低2位为00(即地址是4的整数倍 如int型)
- 双字(8字节) 数据的起始字节地址的最低3位为000(即地址是8的整数倍 如double型)
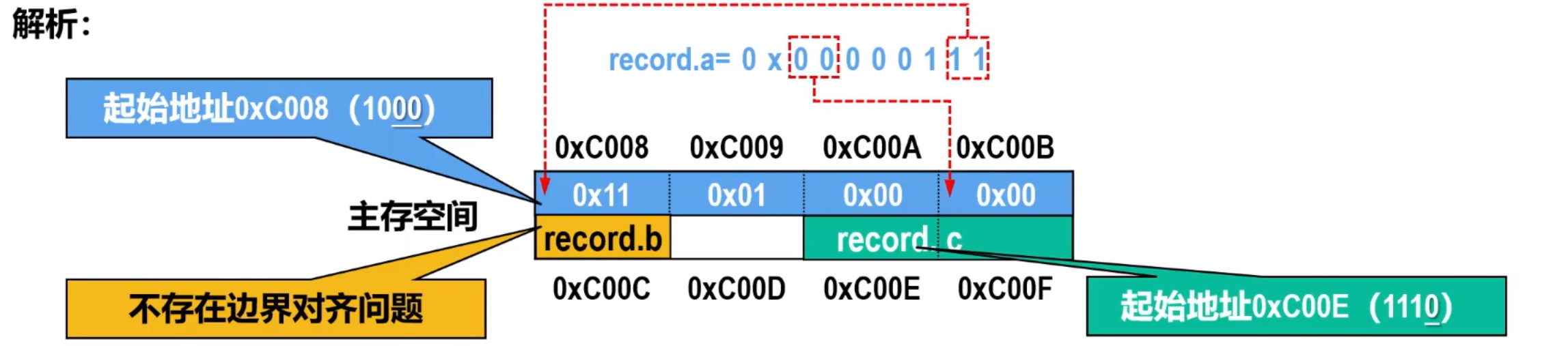
【2012考研 题15】某计算机存储器按字节编址,采用 小端方式 存放数据。假定编译器规定int型和short型长度分别为32位和16位,并且 数据按边界对齐 存储。某C语言程序段如下:
struct { |
若record变量的 首地址为0xC008 ,则地址0xC008中内容及record.c的地址分别是( )。
A. 0x00, 0xC00D
B. 0x00, 0xC00E
C. 0x11, 0xC00D
D. 0x11, 0xC00E
record.a=273 转化为十六进制数0x00000111
4.2.1 SRAM 存储元
静态随机存取存储器
- 静态随机存取存储器 即SRAM (Static Random-Access Memory) 是随机存取存储器的一种
- 所谓 “静态” ,是指这种RAM只要保持通电,其内部所存储的数据就可以保持不变,而 不需要 进行 周期性地刷新 。相比之下,动态随机存取存储器DRAM(Dynamic Random-Access Memory)则需要。
- 目前,SRAM内部的存储元(存储1个二进制位的单元)一般采用多个金属-氧化物半导体场效应晶体管MOSFET(Metal-Oxide-Semiconductor Field-Effect Transistor)来构建,MOSFET常简称为 MOS管 。
- 一旦断电,SRAM和DRAM内部存储的数据还是会消失的,也就是说 SRAM和DRAM属于易失性存储器 ,这与属于非易失性存储器的只读存储器ROM(Read-Only Memory)是不同的。
工作原理及特点
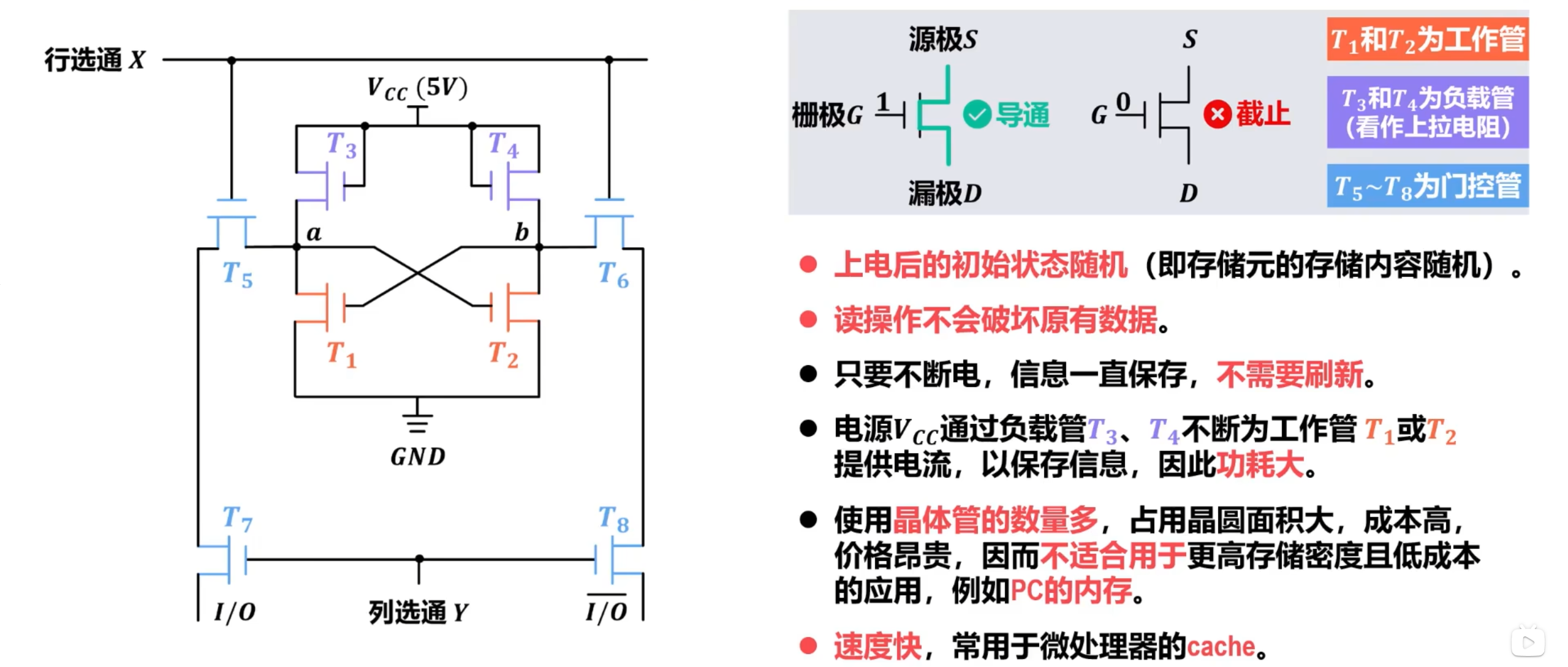
4.2.2 SRAM 存储元扩展和存储阵列扩展
存储元扩展
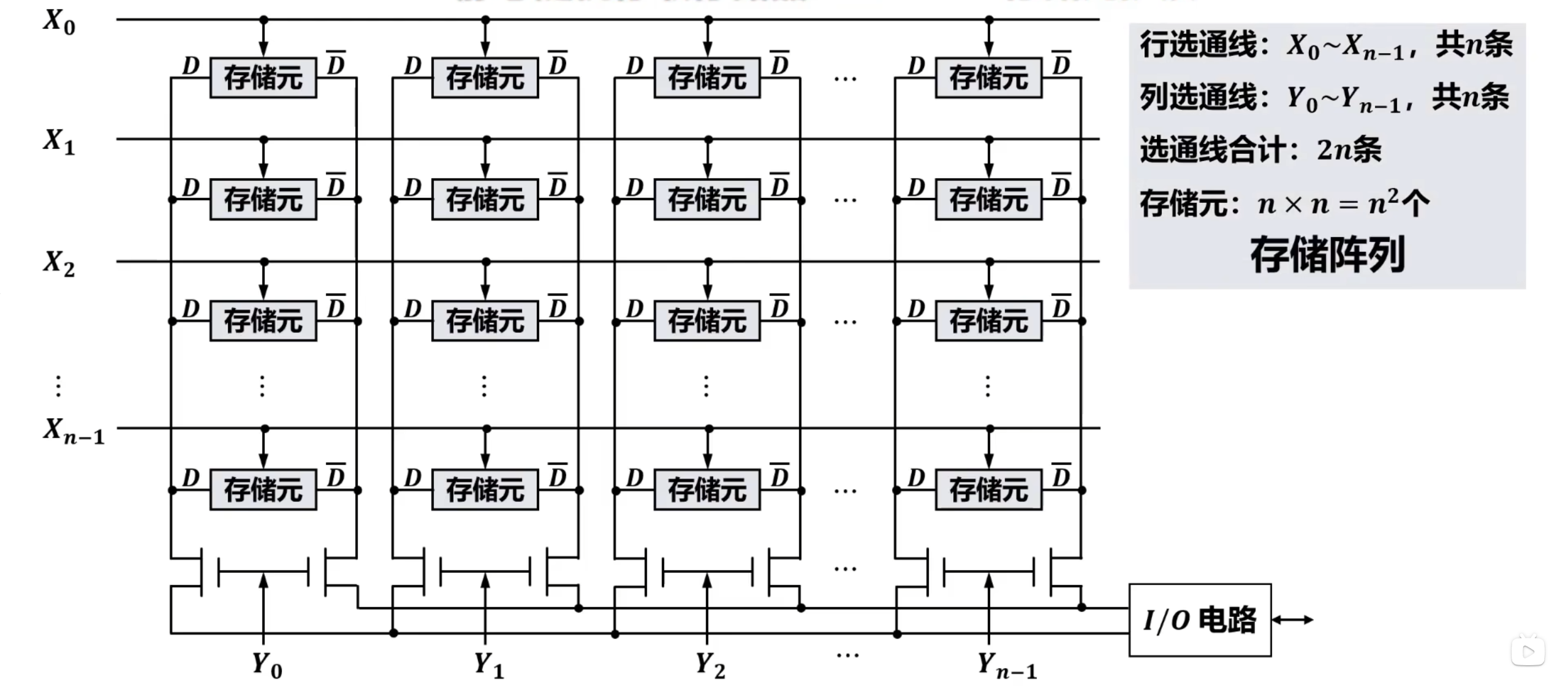
- 若想一次访问多个存储元,须 将多个存储阵列的行选通线并联、列选通线并联
同一时刻,只能有一条行选通线和一条列选通线输出有效信号,因此只能有一个存储元被选中,也就是一次只能访问一位数据。
存储阵列扩展
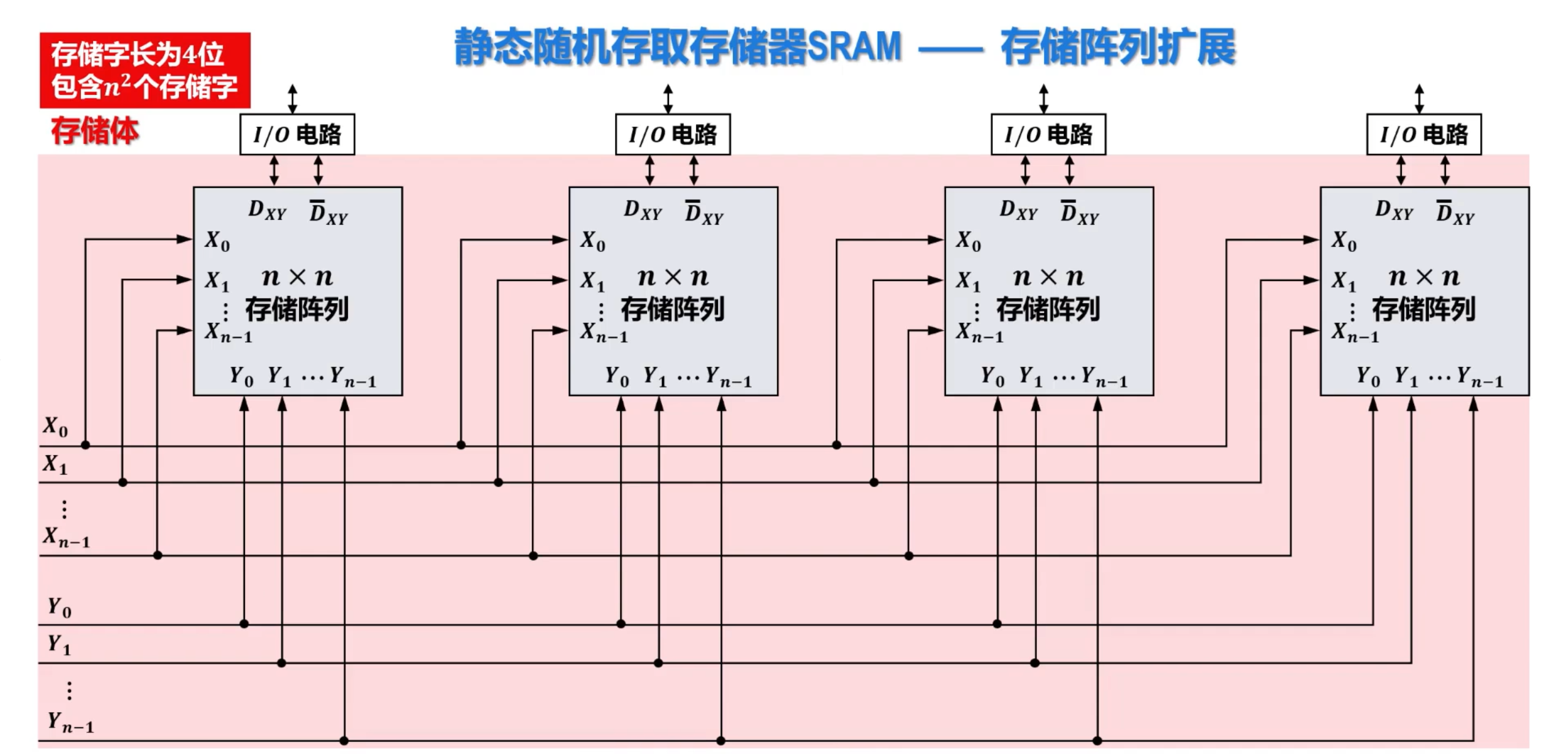
4.2.3 SRAM 存储器结构及其芯片实例
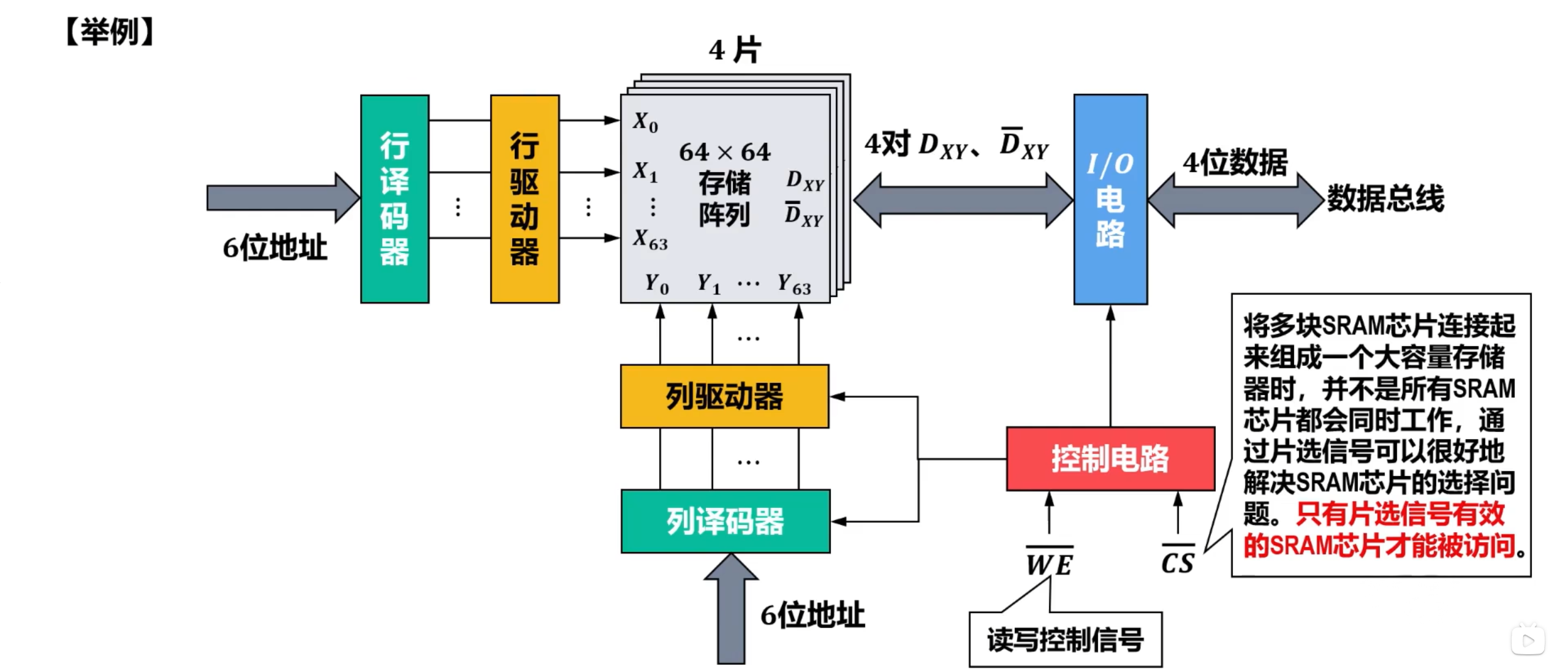
每个型号的SRAM芯片有其特定的读写周期特性,只有按照其读写周期去访问SRAM芯片,才能保证读写操作的正确性。
【习题1】某SRAM中每个存储单元为8位,则以下描述正确的是( B )。
I. 数据线为8位
II. 地址线为3位
III. 存储字长为8位
IV. 机器字长为8位
A. 仅I、II B. 仅I、III C. 仅II、III D. 仅I、III、IV
本题的 I 和 III 正确,是与存储单元的位数相关
II 地址线的数量用于和存储单元的数量进行对应,即3位地址线能寻址 个地址,与题目无关
IV 机器字长通常指的是CPU一次能够处理的数据位数,与题目无关
【习题2】某SRAM的存储容量为8K × 8位,则地址线和数据线的数量分别为( B )。
A. 8、8
B. 13、8
C. 3、3
D. 8、3
存储容量为8K × 8位,意味着有8K个存储单元,每个存储单元8位,数据线的数量为8。
地址线的数量需要能够寻址到8K个地址,即 ,所以地址线数量为13。
【习题3】某SRAM芯片的容量为256K × 16位,除电源和接地端外,该芯片的引脚的最小数目为( D )。
A. 33
B. 34
C. 35
D. 36
由上两题的经验易得地址线为18 ( )
数据线为16位,控制信号 WE和CS 2个
加起来为36
4.3.1 DRAM 存储元及其扩展
动态随机存取存储器
-
动态随机存取存储器,即 DRAM
-
相较于SRAM,设法 减少MOS管 ,通过 引入存储电容 暂存电荷的方式来保存数据
-
目前在内存中较为常见的结构是 单MOS管 和 电容 构成的DRAM存储元
-
存储元工作原理
- 栅极G和源极S接入高电平为电容充电
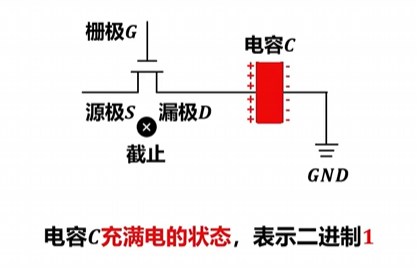
- 此时MOS管打开,栅极G接入高电平而源极没有,则电容通过MOS管放电
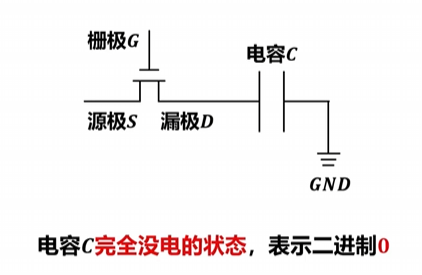
- 上述电容C放电过程,可看作是对存储元的 读操作 ,可以发现,读操作会导致原本存储的1读取后变成0。为避免读操作导致的 数据丢失 ,数据1读出后应将数据1重新写入,称为数据恢复。
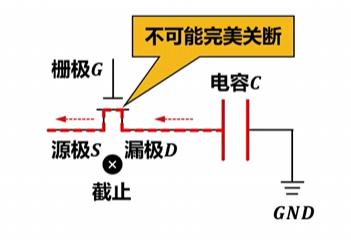
- 由于MOS管不可能完美关断, 电容C上的电荷会逐渐泄露 ,数据1只能保存较短的时间。为避免数据丢失,必须定期采用类似“读操作”的方式对电容C补充电荷,称为刷新,这也是动态RAM(DRAM)得名的原因。
存储元扩展
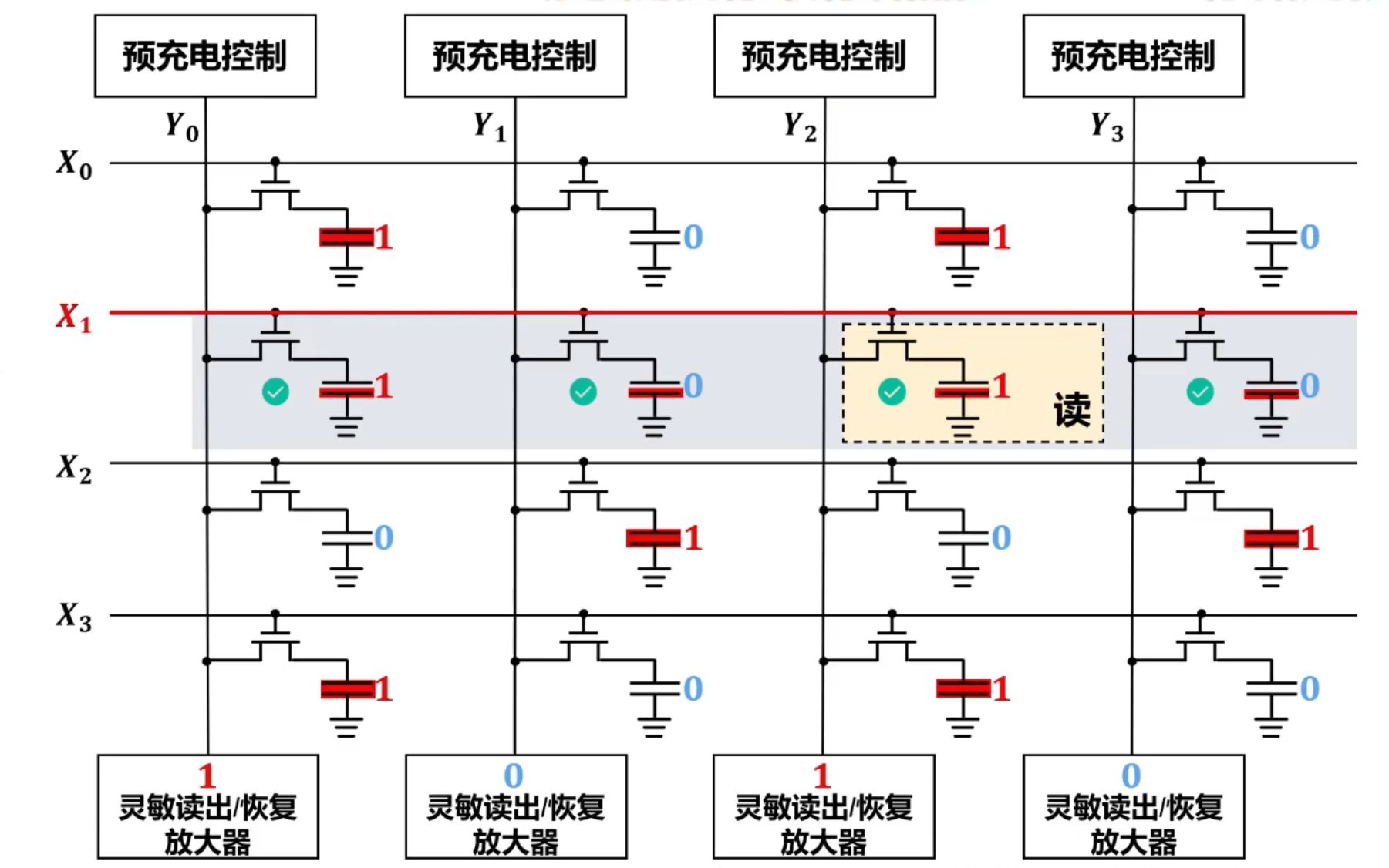
- 为了读取一行中某个存储元的信息, 却破坏了这一行中所有存储元的信息 。
- 因此, 每次读操作过后,必须立即进行写操作 。
- 灵敏读出/恢复放大器会根据锁存的值,将各条列线拉高到DRAM的工作电压 ,或拉低到 ,以恢复各存储元中电容的原本状态(即原本存储的信息)。
读/写流程
DRAM的读操作流程:
- 预充电操作
- 访问操作
- 信号检测
- 数据恢复
- 数据输出
DRAM的写操作流程:
- 预充电操作
- 访问操作
- 信号检测
- 数据恢复
- 数据输入
- 写操作流程需要经历与读操作前4步一样的流程,这样, 写入操作也可以实现和读操作一样的行刷新功能 。
DRAM和SRAM的对比
| 对比项目 | 动态随机存取存储器DRAM | 静态随机存取存储器SRAM |
|---|---|---|
| 构成存储元的元件 | 1个MOS管 和 1个电容 | 6个MOS管 |
| 读操作后需要“数据恢复” | 需要(读操作会改变原本存储的信息) | 不需要(读操作不改变原本存储的信息) |
| 需要动态“刷新” | 需要(电容的电荷会泄露) | 不需要(功耗管和工作管负责保持存储状态) |
| 送行列地址 | 分两次送(地址线复用,减少地址线) | 同时送 |
| 运行速度 | 较慢 | 快 |
| 集成度 | 高 | 低 |
| 发热量 | 小 | 大 |
| 存储成本 | 低 | 高 |
| 可保存性 | 易失性存储器(断电后信息丢失) | 易失性存储器(断电后信息丢失) |
| 常用应用 | 主存 | cache |
4.3.2 DRAM 动态刷新
基本概念
刷新周期
- 从数据存入DRAM开始,到数据丢失之前为止的这段时间,称为最大刷新周期。
- 采用不同材料以及不同生产工艺生产的DRAM,其最大刷新周期可能不同,常见的有2ms、4ms、8ms等。
- 刷新周期是DRAM实际完成两次完整刷新之间的时间间隔。
- 刷新周期 ≤ 最大刷新周期。
刷新存储元的数量
- DRAM按行进行刷新。
- 为了缩短刷新周期,可减少存储阵列的行数,增加列数。
- 刷新操作由内存控制器负责。
刷新与读操作的区别
- 尽管读操作也具有刷新功能,但读操作与刷新操作又有所不同,刷新操作只需要给出行地址,而不需要给出列地址。
刷新方式
DRAM在刷新时,是不能响应CPU的访问的,因此CPU对DRAM进行访问与内存控制器对DRAM进行刷新操作就存在内存争用问题,可采用集中刷新、分散刷新、异步刷新等刷新方式来解决。
【举例】假设DRAM存储体的结构为128行 × 128列,存取周期为0.5微秒(μs),刷新周期为2毫秒(ms),下面给出集中刷新、分散刷新以及异步刷新三种刷新方式。
-
通过上节课的介绍我们知道,刷新操作与读操作是类似的,本例给定存取周期为0.5μs,则刷新一行所需的时间也为0.5μs。
-
本例给定刷新周期为2ms,也就是在2ms内,要完成所有128行的刷新。
综上所述,将2ms(2000μs)划分成4000个0.5μs长的时隙,在这些时隙中选出128个时隙,每个时隙刷新一行即可。
集中刷新

- 读写操作期间不受刷新操作的影响,因此这段时间的访问速度比较快。
- 但是,在集中刷新的这128个时隙中,CPU长时间不能访问DRAM,这段时间称为**“死区”时间**。
- 存储体包含的行数越多,“死区”时间就越长。
分散刷新

- 相当于将存取周期加上刷新1行的时长作为新的存取周期,因此不存在“死区”时间。但是,这种方式刷新过于频繁(在2ms所包含的4000个时隙中,有2000个时隙用于刷新,每个时隙刷新1行,共刷新2000行,每刷新128行,就相当于把存储体完整地刷新了1遍,因此在2ms内进行了约15次完整的存储体刷新),严重影响了系统的速度。
- 不适合应用于高速存储器。
异步刷新

- 既充分利用了2ms时间,又保持系统高速特性。该方式缩短了死区时间(128个时隙缩短为1个时隙),该方式相对上述两种效率更高,更为常用。
【习题1】DRAM按( C )进行刷新。
A. 存储元
B. 存储体
C. 行
D. 列
【习题2】以下DRAM刷新方式中,存在明显“死区”时间的是( B )。
A. 异步刷新
B. 集中刷新
C. 分散刷新
D. 以上都不是
【习题3】假设DRAM存储体的结构为64行 × 64列,存取周期为0.5μs,刷新周期为2ms,若采用集中刷新方式,则在刷新周期内,可用于读写或保持状态的连续时长为( C )。
A. 32μs
B. 64μs
C. 1968μs
D. 3936μs
在集中刷新中,
而
4.3.3 DRAM 存储器芯片实例及其发展
DRAM 存储器芯片实例
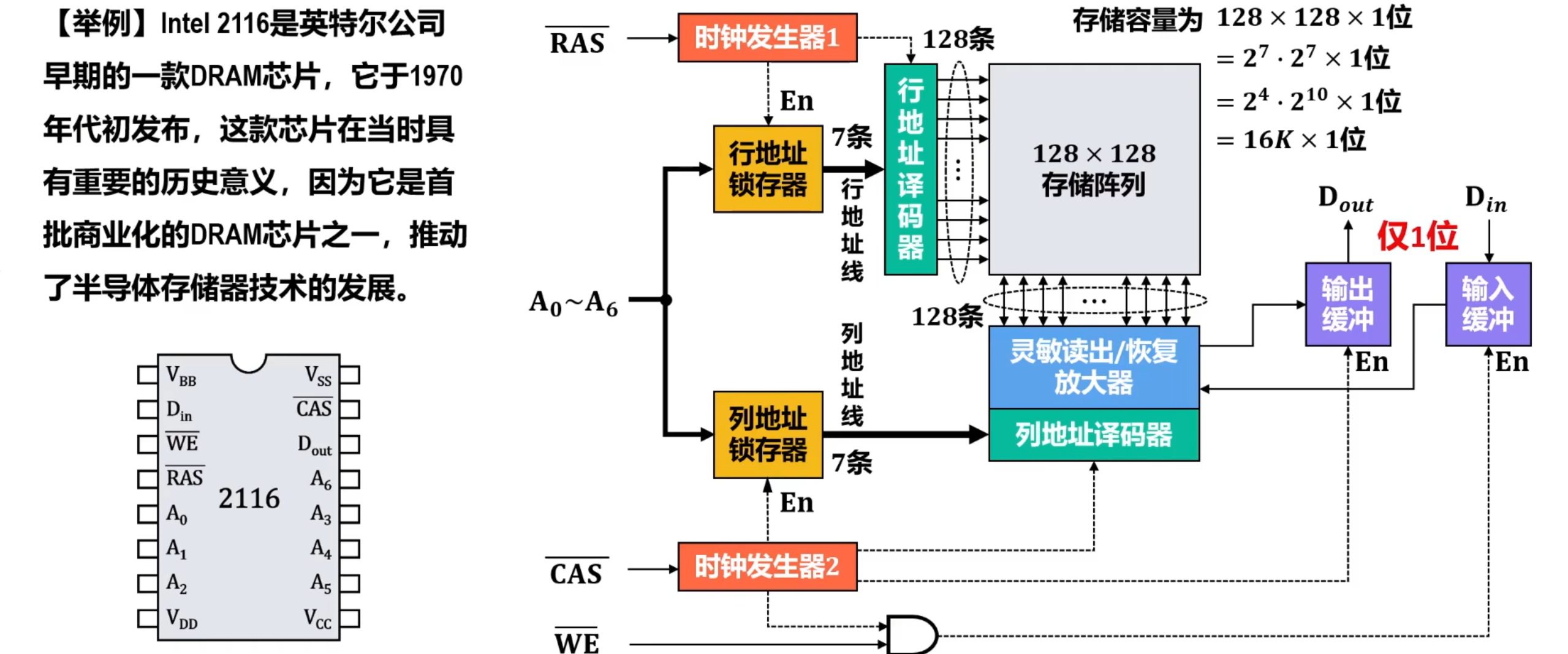
【习题】某个DRAM芯片,其容量为1K × 1位,采用地址复用技术,读写控制线为一条,除电源和接地引脚外,该芯片的引脚数最小是(B)。
A. 8
B. 9
C. 10
D. 11
- 1K = 2^10 因此共需要10条地址线(例如行地址线和列地址线各5条)
- 题目给定采用地址复用技术,因此地址线为5条,由行地址线和列地址线共同使用。
- 需要行地址选通线、列地址选通线、读写控制线各1条。
- 还需要1条数据I/O线。
【2014考研 题15】某容量为256MB的存储器由若干4M × 8位的芯片构成,该DRAM芯片的地址引脚和数据引脚总数是(A)。
A. 19
B. 22
C. 30
D. 36
- 4M = 2^2 × 2^20 = 2^22 因此共需要22条地址线(例如行地址线和列地址线各11条)
- 由于DRAM采用地址复用技术,因此地址线为11条,由行地址线和列地址线共同使用。
- 还需要8条数据I/O线。
【2018考研 题17】 假定DRAM芯片中存储阵列的行数为r、列数为c,对于一个2K × 1位的DRAM芯片,为保证其地址引脚数最少,并尽量减小刷新开销,则r、c的取值分别是(C)。
A. 2048、1
B. 64、32
C. 32、64
D. 1、2048
- 2K = 2 × 2^10 = 2^11
- 因此共需要11条地址线
- 由于DRAM采用地址复用技术,因此地址线为6条,由行地址线和列地址线共同使用:
- 方案1:若行地址线为6条,则可译码出2^6 = 64条行线;列地址线为5条,则可译码出2^5 = 32条列线。
- 方案2:若行地址线为5条,则可译码出2^5 = 32条行线;列地址线为6条,则可译码出2^6 = 64条列线。
- 由于DRAM按行刷新,为了减小刷新开销,行数应该减少,而增加列数。
DRAM发展
异步DRAM:
- 1970年代初:传统DRAM
- 1990-1995年 486时代和Pentium时代的初期:
- FPM-DRAM
- EDO-DRAM(1995年 Pentium时代的初期)
- 对EDO-RAM的改进 昙花一现:
- BEDO-DRAM
同步DRAM:
- 1996年:SDRAM
- 21世纪:DDR SDRAM
- 异步DRAM的读写操作与CPU的时钟周期无关,在进行读写操作时可能会有更多的等待周期,导致性能上的损失,特别是在CPU的时钟频率很高的情况下。
- 同步DRAM的读写操作与CPU的时钟周期同步,内存控制器可以在时钟信号的特定边缘(上升沿或下降沿)触发数据传输。
SDRAM 读操作

- SDRAM自带时钟信号,能与系统总线频率同步。
- SDRAM可以突发(Burst)传输:第一个列数据就绪后,每经历一个时钟周期就可得到一个数据,有效减少了数据传输的时间延迟。
- 通常SDRAM包含有模式寄存器,可配置突发传输的长度BL(Burst Length),例如1、2、4、8以及整行字。该长度是同步地向系统总线上发送数据的存储单元的个数。
- 传统DRAM没有突发传输模式,每访问一个数据,就要经历行地址、列地址、访问数据的过程。
- 传统DRAM属于异步DRAM,其读写操作与CPU的时钟周期无关,在进行读写操作时可能会有更多的等待周期,导致性能上的损失,特别是在CPU的时钟频率很高的情况下。
DDR SDRAM
-
在SDRAM之后出现的DDR SDRAM(Double Data Rate SDRAM),其内部采用了2路预取机制,第一个数据输出后,每个时钟周期可传输两次数据,即在时钟周期的上升沿和下降沿分别进行一次数据传输,从而实现双倍数据传输速率。
-
在DDR SDRAM之后,又陆续出现了DDR2、DDR3、DDR4,其内部预取分别是4路、8路、16路,即同一个时钟周期可传输4、8、16个数据,可理解成:每个时钟周期传输两次数据,每次传输2个、4个、8个数据。
- 这就需要提高数据总线频率来实现高速的数据传输,DDR2的数据总线频率是DRAM工作频率的2倍,DDR3则为4倍,DDR4则为8倍。
-
【举例】以内存规格DDR4 - 3200为例。
- 3200为等效传输频率(单位为MHz)
- 数据位宽(64b)
- 内存带宽(传输率)=
- 由于时钟上升沿和下降沿各完成一次数据传输,因此数据总线频率 =
- DRAM工作频率 =
4.4.1 ROM 只读存储器
-
只能从其读出信息、而不能向其随意写入信息的存储器,称为只读存储器(Read-only Memory,ROM)。
- 通过特定方式将信息写入ROM后,信息就固定在ROM中,即使电源断电,所保存的信息也不会丢失,也就是说,ROM属于非易失性存储器。
-
按照制造工艺的不同,ROM可分为:
-
掩膜式只读存储器(Mask ROM,MROM)
- 待存储信息由芯片制造厂家在生产过程中按用户要求做好,芯片制成后存储信息被固定在芯片中,因而只能读出,不能修改。
- 灵活性差,但所存储的信息固定不变,可靠性高。
-
可编程只读存储器(Programmable ROM,PROM)
- 存储器出厂时,每个存储元存储的数据为“0”,用户可利用编程器进行一次改写。
- PROM克服了MROM使用不便的问题,但仅能改写一次,灵活性还是不够。
-
可擦除可编程只读存储器(Erasable Programmable ROM,EPROM)
- 可多次写入,重新写入时需要先擦除后写入。
- 需要使用紫外线照射来擦除全部存储元的状态。
- EPROM比PROM和MROM使用方便、灵活、经济。
-
电可擦除可编程只读存储器(Electrically Erasable Programmable ROM,EEPROM或E²PROM)
- 可多次写入,写入方式与EPROM相同,但不需要先擦除后写入。
- 因为擦除时不用紫外线照射,采用电可擦除方式(根据命令,内部自动完成),可以精准地擦除某一个存储元,而非全片擦除。
- 常用于存储MAC地址、存储BIOS。
-
闪存(Flash Memory)
- 逻辑结构与EEPROM相似,但存储元的结构和工艺不同。
- EEPROM支持字节级擦写,适合频繁更新小数据量,而闪存以块为单位擦写(先擦后写,因此读快写慢),更适合存储大量数据。
- 常用于SD卡、U盘、SSD、存储BIOS。
-
4.4.2 PC中的半导体存储器
-
非易失性存储器:
-
主板中的BIOS芯片(NOR型内存或EEPROM)
用于存储计算机启动时所执行的固件(例如BIOS或UEFI)的存储器,目前主流为闪存,启动固件负责初始化硬件、硬件检测并加载操作系统到主存中的RAM,以便CPU可以执行操作系统的代码,从而开始操作系统的运行。
-
SSD的多片存储芯片(NAND型闪存)
用于存储操作系统、应用程序、用户数据的闪存,属于辅存(外存)。
-
-
易失性存储器:
-
CPU的内部cache(SRAM静态随机存取器)
通常采用SRAM(无需动态刷新)作为CPU和主存之间的高速缓存,减少CPU访问主存的次数,提高数据处理速度。
-
内存条的多片存储芯片(DDR4 SDRAM)
用于存储CPU执行的指令和用户数据的存储器。
-
4.5.1 主存的扩展及其与CPU的连接 位扩展
由下图CPU可见,R/W#的"#"表示低电平有效,也就实现了和 引脚的对应
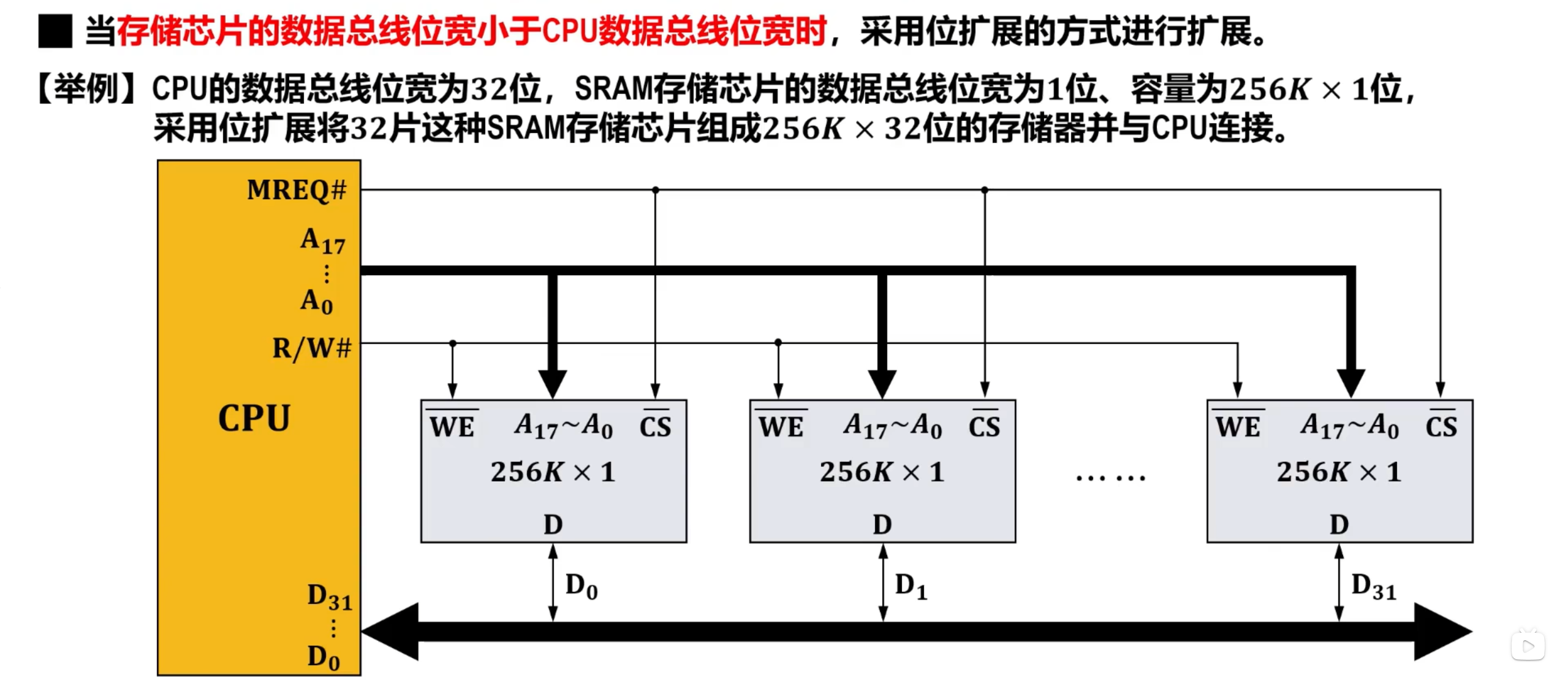
初始状态
初始状态时,由于MREQ#的输出,存储芯片处于不被选中工作状态
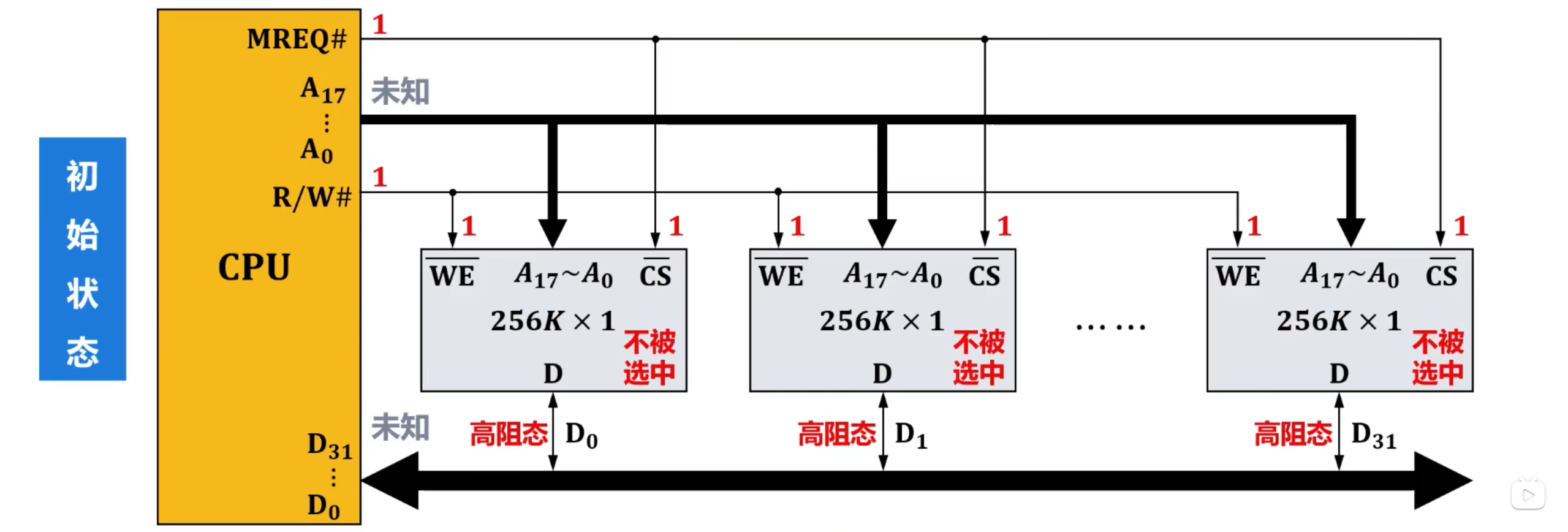
读操作
-
若要进行读操作,CPU的地址总线送出相应位数的地址,各存储芯片通过各自的地址引脚收到地址
-
当存储芯片被同时选中工作时,其各自内部该地址所对应的存储单元被同时选中
-
之后,CPU的存储器控制引脚 输出低电平,各存储芯片的片选引脚 收到该有效电平,因此被选中工作
-
由于CPU的输出高电平,各存储芯片将被选中的存储单元存储的1位数据,通过各自的1位数据线,传送到CPU的数据总线中相应的数据线,CPU再通过数据总线读取数据
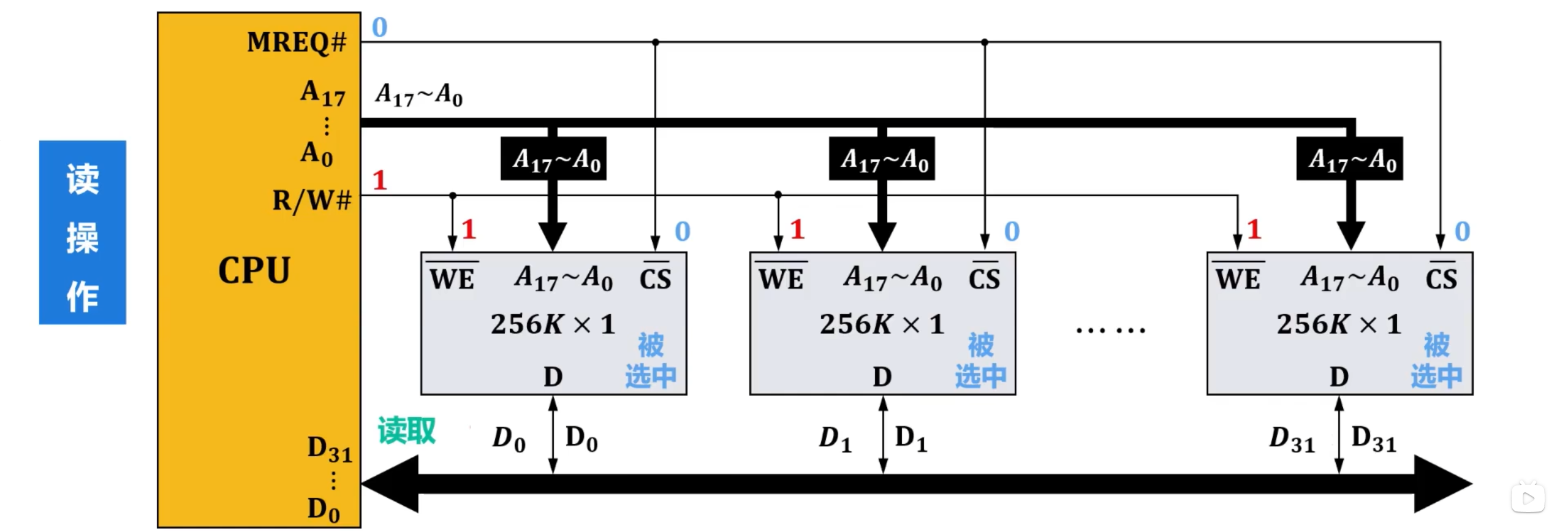
写操作
-
从初始状态进行写操作,从CPU送出待写入主存的数据
-
CPU的地址总线送出相应位数的地址,各存储芯片通过各自的地址引脚收到地址
-
当各存储芯片被同时选中工作时,其各自内部该地址所对应的存储单元被同时选中
-
之后,CPU的 输出低电平,各存储芯片的使能引脚 收到该低电平,但由于存储芯片不在工作状态,暂不理会此信号
-
之后,CPU的存储器控制引脚 输出低电平,各存储芯片的片选引脚 收到该有效电平,因此被选中工作
-
各存储芯片通过各自的1位数据线,从CPU的数据总线中相应的数据线上,读入一位数据,并写入选中的存储单元
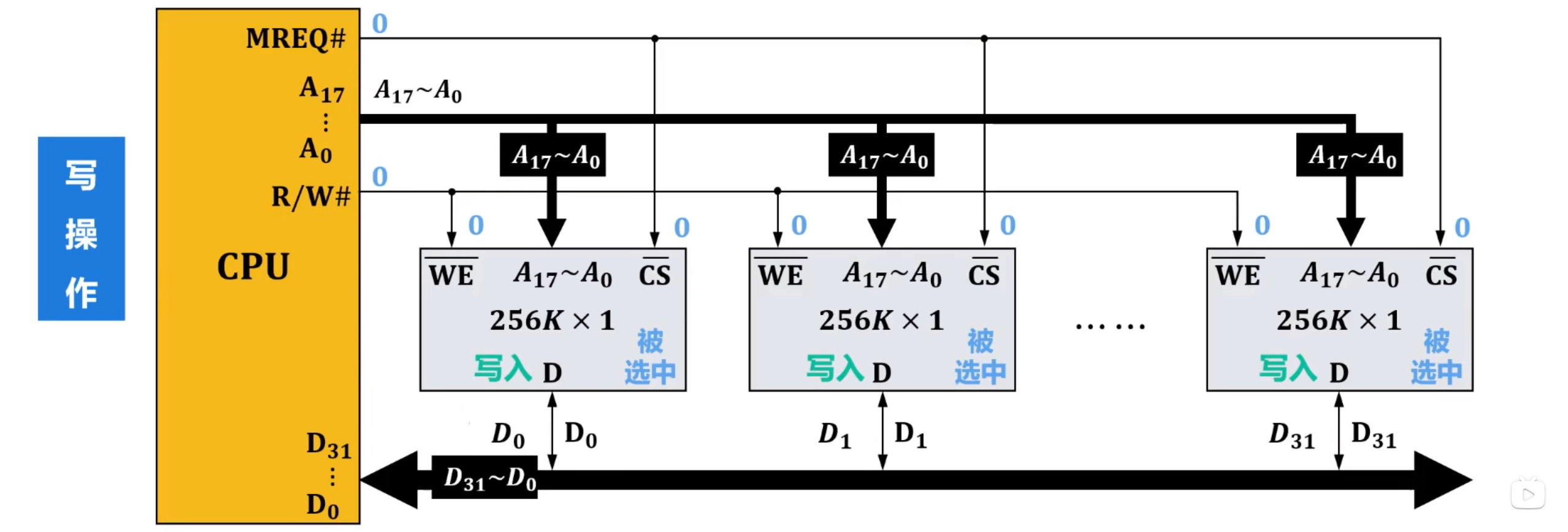
总结
- 将所有存储芯片的地址引脚、写使能引脚 分别并联后再分别与CPU的地址引脚和读写控制引脚 连接;
- 将各存储芯片的数据引脚依次与CPU的数据引脚进行相应连接;
- 将所有存储芯片的片选引脚 并联后与CPU的存储器请求控制引脚 相连。
综上所述,位扩展又称为数据总线扩展或字长扩展。
4.5.2 主存的扩展及其与CPU的连接 字扩展
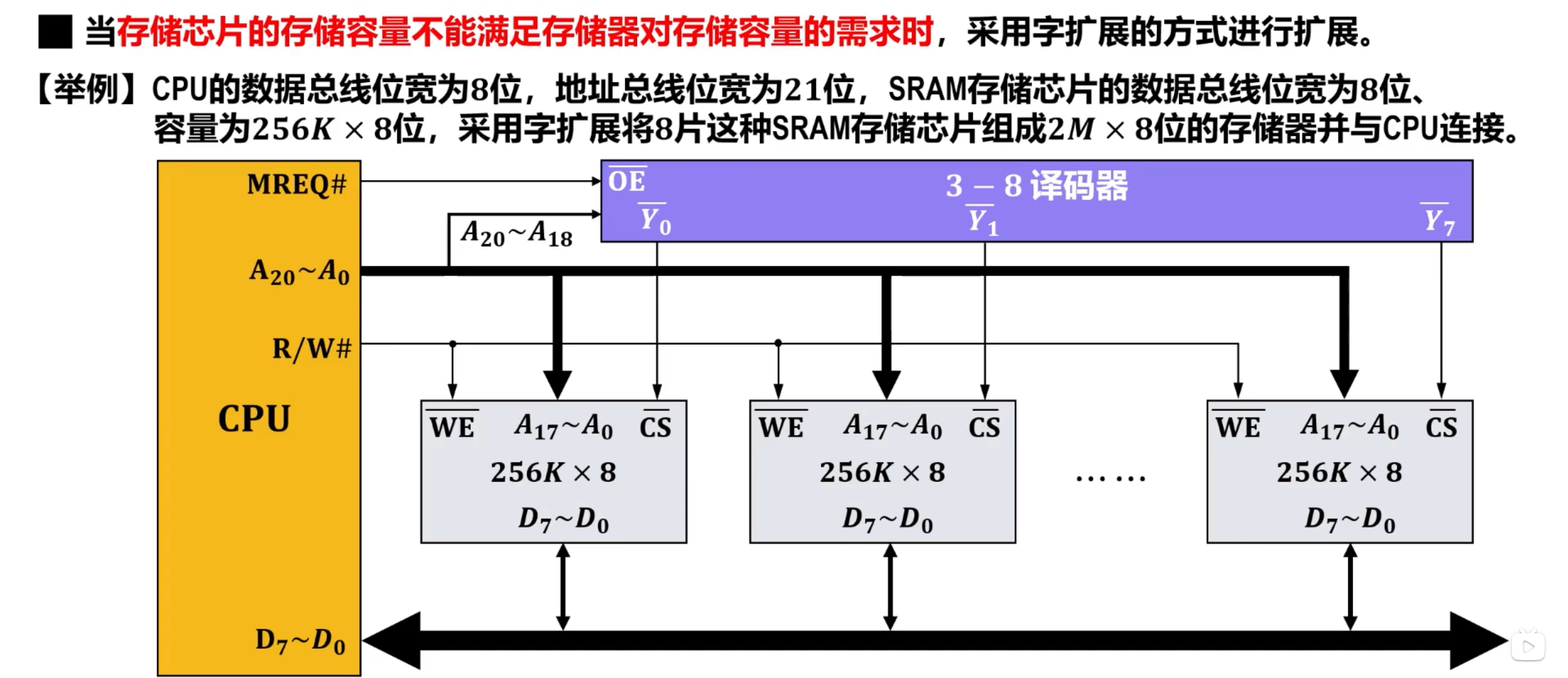
初始状态
- CPU的存储器请求控制引脚 输出无效电平,也就是高电平,使得3-8译码器的8个译码输出全部都为无效电平
- 各存储芯片的片选引脚 收到该无效电平,因此不被选中工作,进而各自的8位数据总线输出为高阻态
- CPU的读/写控制引脚 输出高电平,各存储芯片的写使能引脚 收到该高电平
- 由于各存储芯片都未被选择工作,因此不会理会该信号
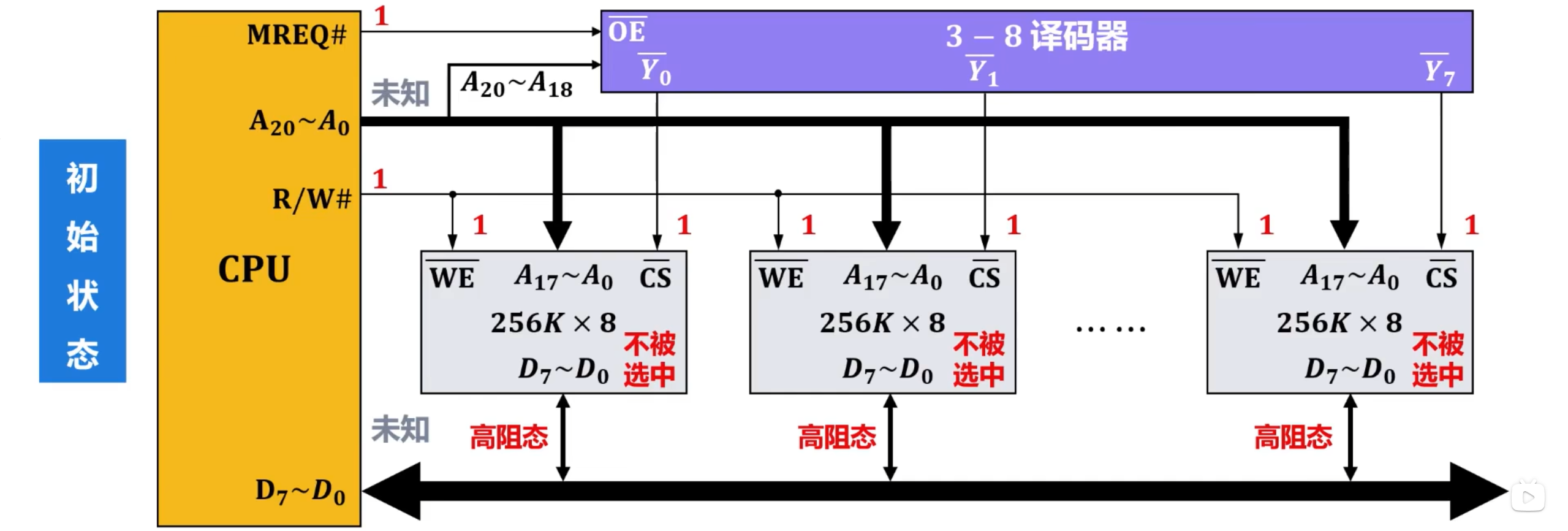
读操作
- CPU的21条地址总线送出21位的地址,其中各存储芯片都会通过各自的18个地址引脚收到这21位地址的低18位
- 而3-8译码器的3个译码输入引脚收到高3位地址,假设这个高3位地址为
- 之后CPU的存储器请求控制引脚 输出低电平,3-8译码器的输出使能引脚 收到该低电平时,将3位译码输入,译码成8位译码输出,具体为输出有效信号,也就是低电平,而到仍保持输出无效信号,也就是高电瓶。
- 这样,8片存储芯片中,只有片选引脚 收到有效电瓶的该存储芯片被选中工作,而该存储芯片通过自身18个地址引脚收到的18位地址所对应的存储芯片内部的那个存储单元被选中。
- 由于此时该存储芯片的写使能引脚 上的信号是之前由CPU的读写控制引脚 输出的高电平,因此该存储芯片将被选中的存储单元中存储的8位数据,通过自己的8位数据总线传送到CPU的8位数据总线。
- 由于此时剩余7片存储芯片都未被选中工作,因此他们各自的8位数据总线处于高阻态,不会对CPU的8位数据总线产生影响。
- 之后,CPU通过8位数据总线读取8位数据。
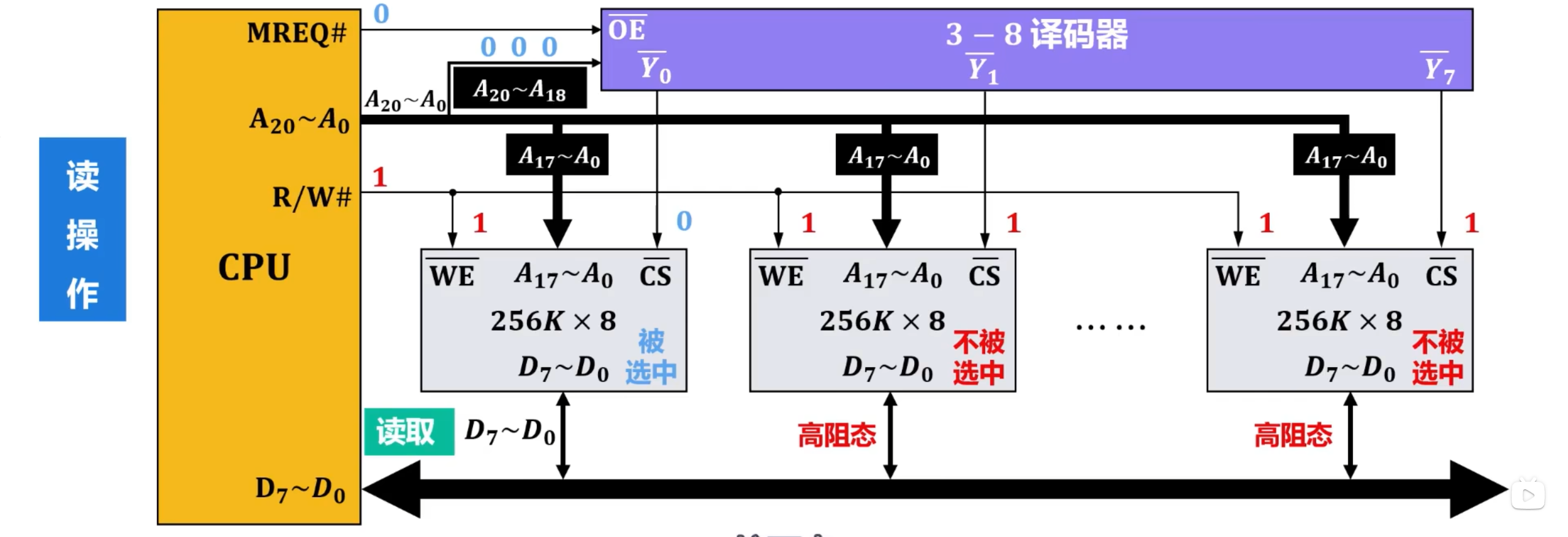
写操作
- CPU的21条地址总线送出21位的地址,其中各存储芯片都会通过各自的18个地址引脚收到这21位地址的低18位
- 而3-8译码器的3个译码输入引脚收到高3位地址,假设这个高3位地址为
- 之后,CPU的读写控制引脚 输出低电平,各存储芯片的写使能引脚 收到该低电平。由于各存储芯片此时都未被选中工作,因此不会理会该信号。
- 之后,CPU的存储器请求控制隐角 输出低电频。3-8译码器的输出使能引脚 收到该低电平时,将3位译码输入译码成8位译码输出。
- 具体为 输出有效信号,也就是低电平。而 到 仍保持输出无效信号,也就是高电频。
- 这样,8片存储芯片中,只有片选引脚 收到有效电平的该存储芯片被选中工作。而该存储芯片通过自身18个地址引脚收到的18位地址,所对应的存储芯片内部的那个存储单元被选中。
- 由于此时该存储芯片的写使能引脚 上的信号是之前由CPU的读写控制隐角 输出的低电平。因此,该存储芯片通过自身的8位数据总线,从CPU的8位数据总线获取到8位数据,并写入所选中的存储单元。
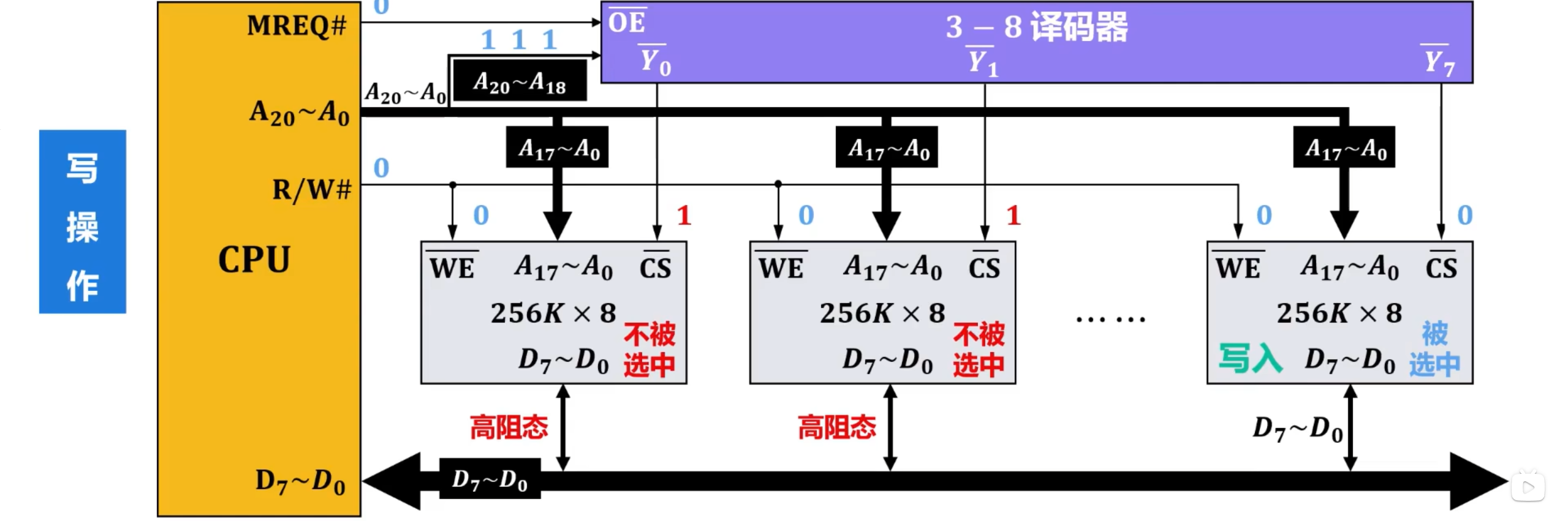
寻址
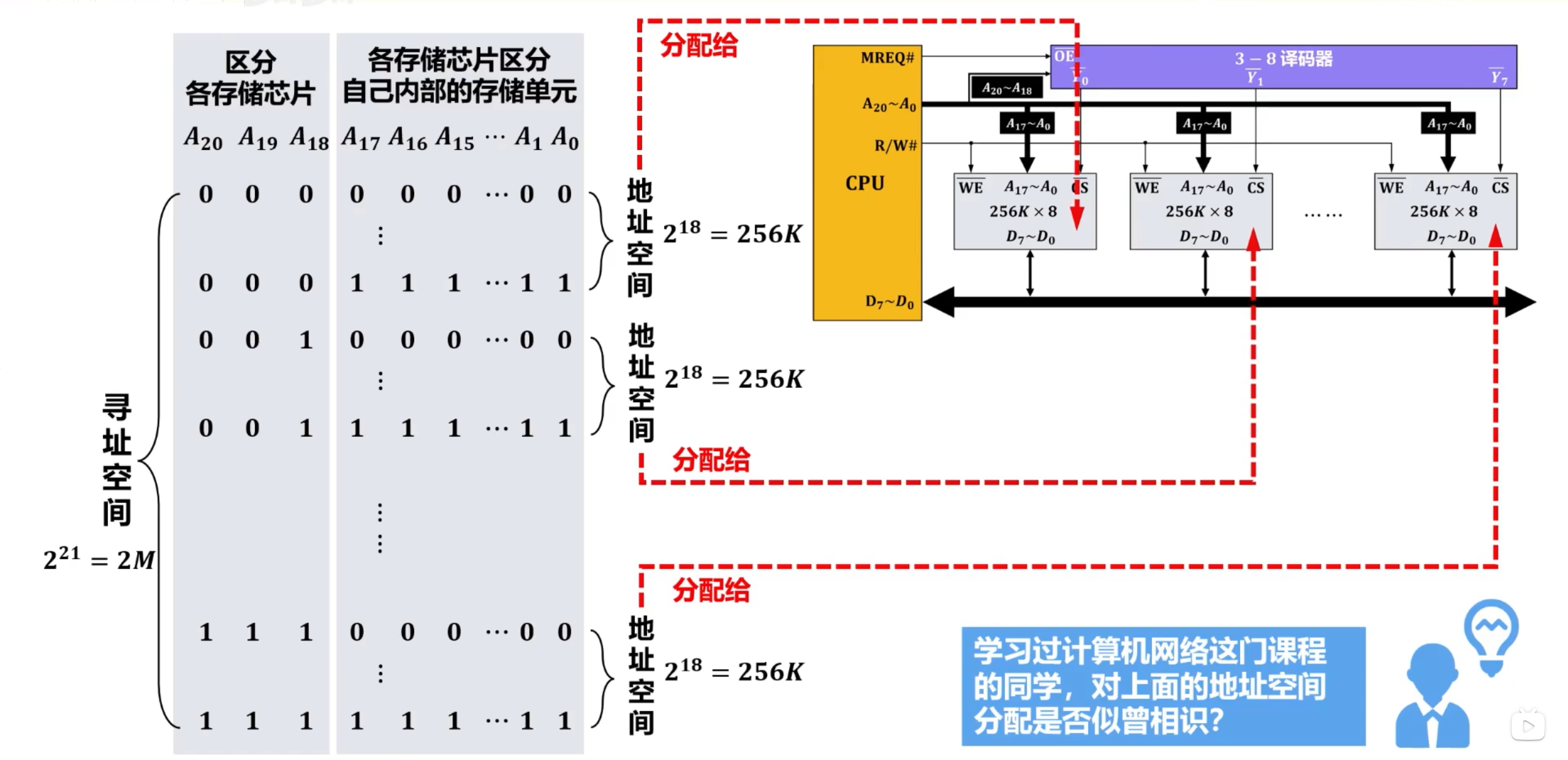
总结
-
将所有存储芯片的数据引脚、地址引脚、写使能引脚 各自并联后再分别与CPU的数据引脚、地址引脚、读写控制引脚 连接;
-
各存储芯片的片选引脚 可以由CPU多余的地址引脚通过译码器产生。
-
综上所述,字扩展又称为容量扩展或地址总线扩展。
-
实际的译码器芯片具有更多的使能引脚,以便更灵活地应用。
4.5.3 主存的扩展及其与CPU的连接 字/位同时扩展
- 当存储芯片的数据位宽和存储容量均不能满足存储器的数据位宽和存储总容量要求时,采用字位同时扩展。
- 首先通过位扩展满足数据位宽的要求。
- 再通过字扩展满足存储总容量的要求。
【举例】 CPU的数据总线位宽为32位,地址总线位宽为21位,SRAM存储芯片的数据总线位宽为8位、容量为256K × 8位,采用字位同时扩展将32片这种SRAM存储芯片组成2M × 32位的存储器并与CPU连接。
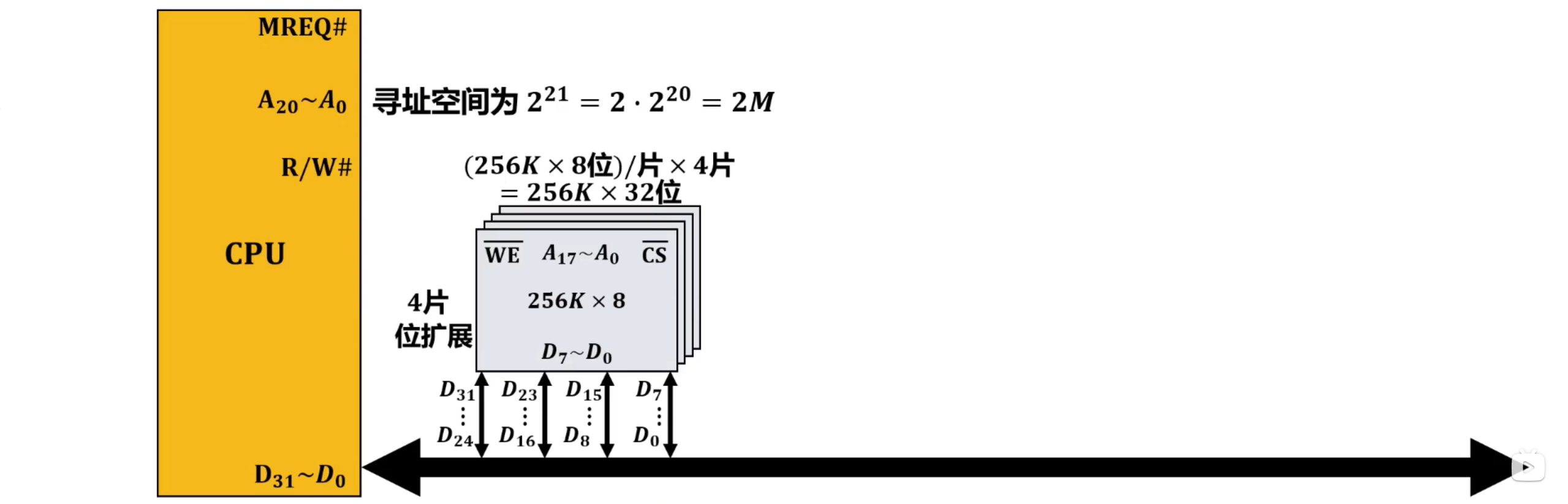
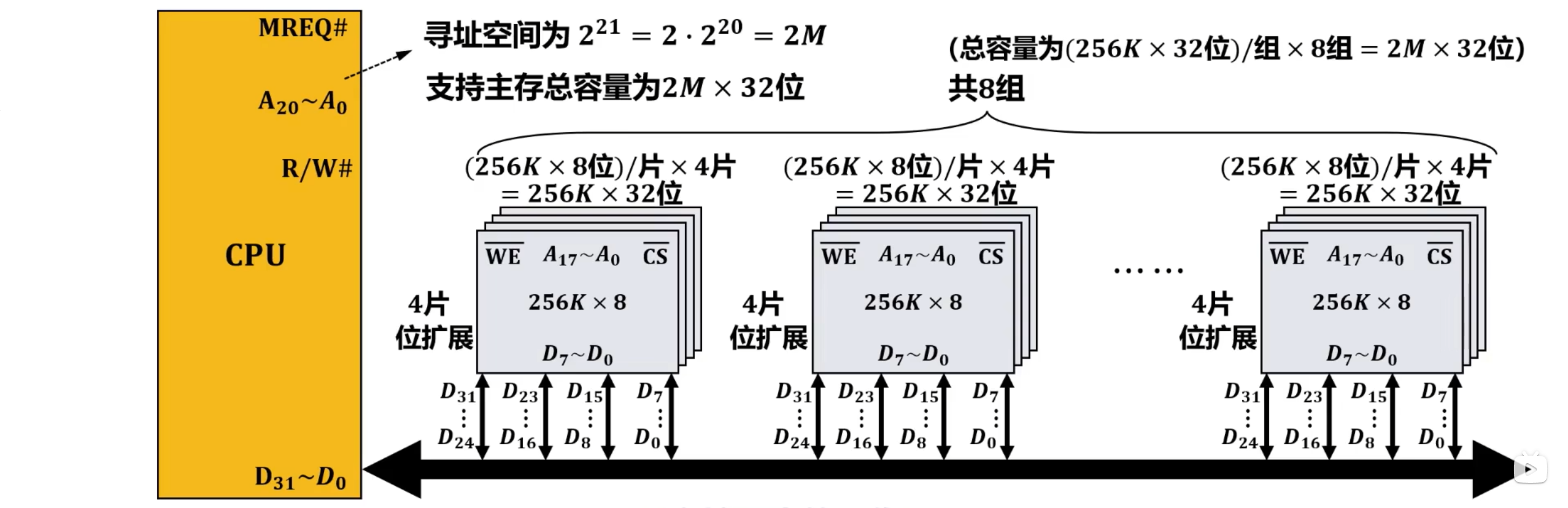
4.5.4 主存的扩展及其与CPU的连接 习题
4.6.1 Cache 基本概念
- 主存一般采用容量大、功耗较小、成本较低的同步动态随机存取存储器SDRAM(目前主流为DDR4或DDR5)。
- 静态随机存取存储器SRAM的容量小、功耗大、成本高,但SRAM的访问速度远高于SDRAM。
- 因此,为了提升CPU访问主存的性能,通常会在CPU与主存之间添加一个SRAM作为高速缓冲存储器cache。
- 将主存中经常访问或即将访问的数据,复制一份**(调度)到cache中,使得大部分数据访问都可以在cache中进行**,从而提升系统性能。
- 采用这种方法的主要原因是CPU执行的程序具有较强的程序局部性。
程序局部性
- 程序局部性是指,在一段时间内,整个程序的执行仅限于一个较小的局部范围内。具体来说,程序的局部性又表现为以下两种:
- 时间局部性:若程序在某个时刻访问了一个存储位置,该位置在未来可能会被多次访问。
- 例如程序中的循环结构和调用过程就很好地体现了时间局部性。
- 空间局部性:若程序访问了某个存储位置,则其附近的存储位置也可能被访问。
- 例如程序中的数组、结构体成员、顺序执行的代码块,通常在主存中是按顺序存放的,对它们的访问,就是具有较强的空间局部性。
- 时间局部性:若程序在某个时刻访问了一个存储位置,该位置在未来可能会被多次访问。
【2017年 考研题14】某C语言程序段如下:
for (i=0; i<=9; i++) { |
下列关于数组a的访问局部性的描述中,正确的是(A)。
A. 时间局部性和空间局部性皆有
B. 无时间局部性,有空间局部性
C. 有时间局部性,无空间局部性
D. 时间局部性和空间局部性皆无
- 数组a中的各元素在主存中顺序存放,具有空间局部性;
- 数组a的读取序列:a[0]、a[0]、a[1]、a[0]、a[1]、a[2]、…数组a中的同一元素被多次访问,具有时间局部性。
Cache系统的性能评价
-
在CPU和主存之间添加了cache后,CPU不再直接访问慢速的主存,而是通过字节地址访问快速的cache
-
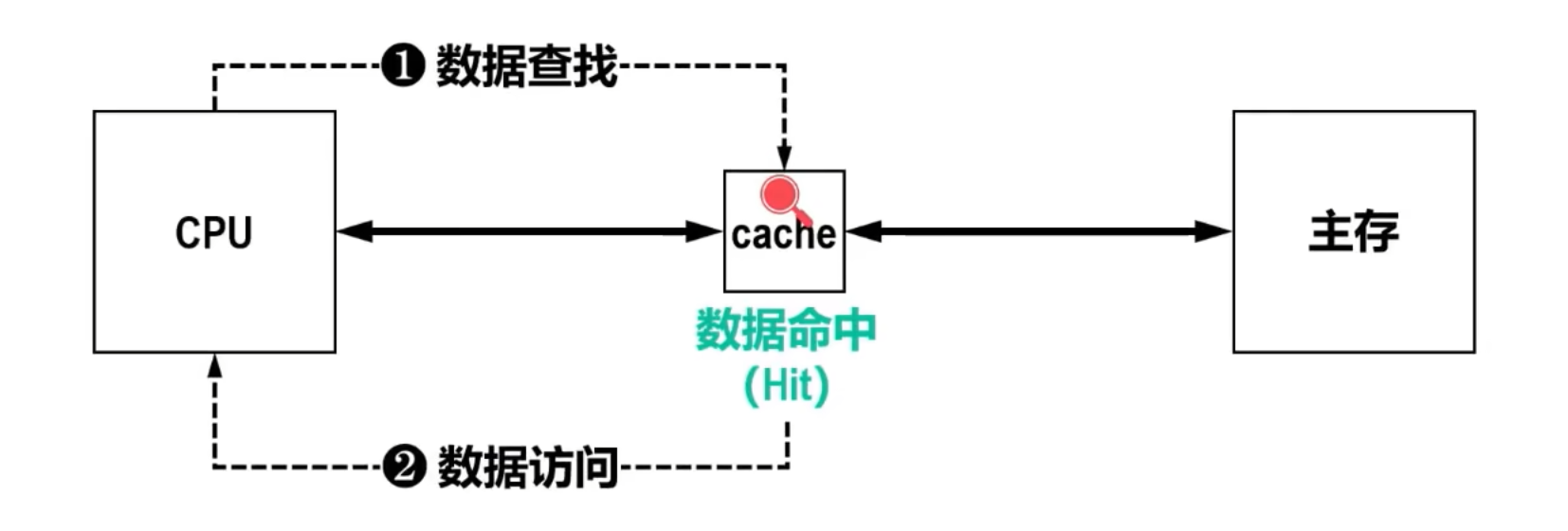
-
上述情况下,数据访问时间称为命中访问时间,记为 (cache内的查找时间/cache访问时间)
-
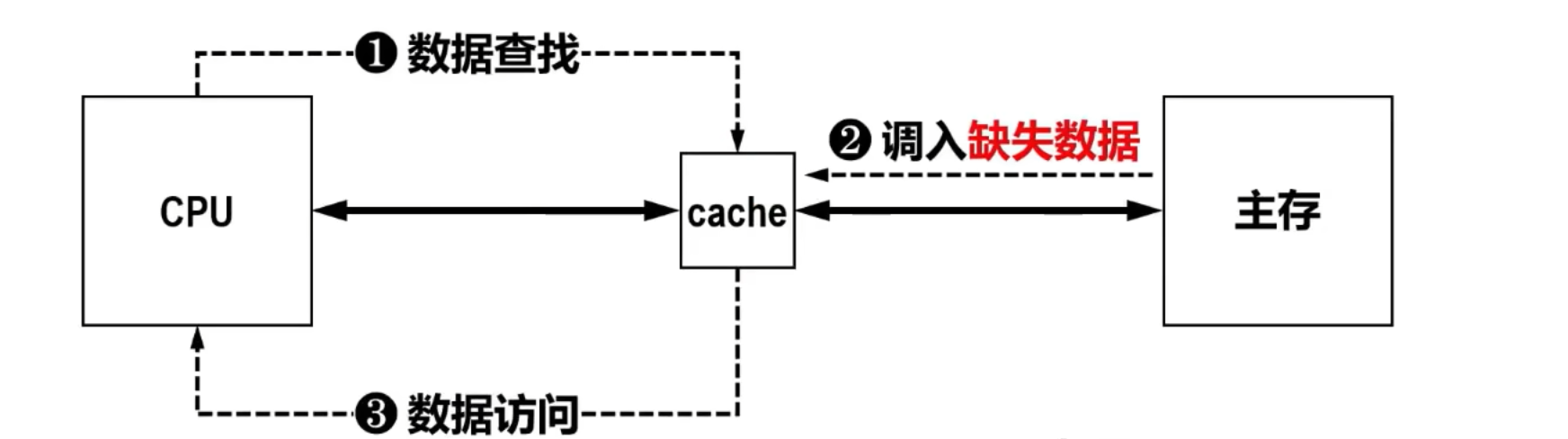
-
上述情况下,数据访问时间称为缺失补偿,记为 (cache内的查找时间/主存访问时间/cache访问时间)
-
-
为了便于快速查找,主存和cache都被划分成若干个固定大小的数据块(Block),每个数据块又包含若干个字。
- 若进行数据访问时出现数据缺失的情况,则需要将缺失数据所在的数据块从慢速主存载入cache中。
- 因此,缺失数据相邻的数据也会随着数据块一起载入cache。
-

-
上述预读策略可以充分利用程序的空间局部性,提高顺序访问的命中率。
-
然而,数据块的大小对cache有较大影响:
- 数据块过小:无法利用预读策略优化程序的空间局部性。
- 数据块过大:将使得替换算法无法充分利用程序的时间局部性。
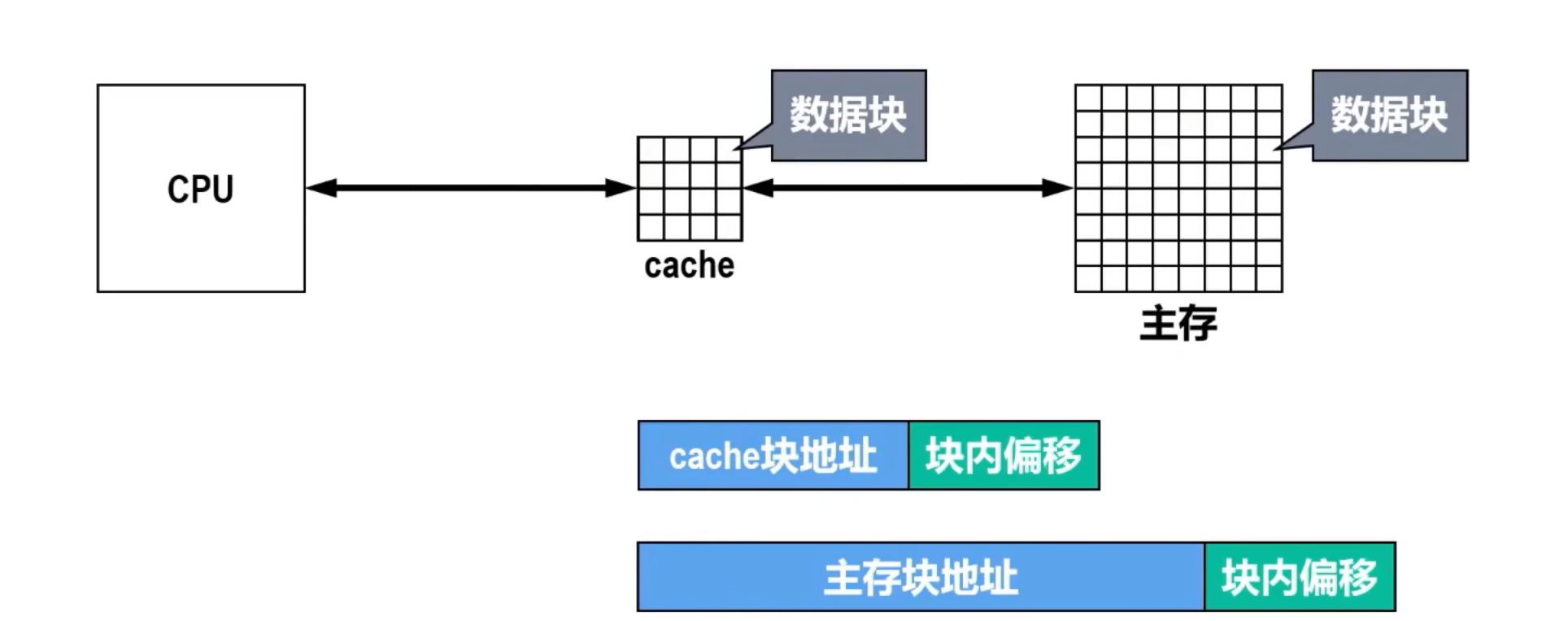
- 进行数据分块后,需要给主存内的数据块和cache内的数据块分配地址。
- 数据块的地址由块地址和块内偏移地址(简称块内偏移Offset)两部分构成。
- 由于cache容量比主存容量小很多,因此cache内的块地址长度小于主存内的块地址长度。
性能评价指标
某程序运行期间命中cache的次数记为 ,从主存中访问信息的次数记为 ,命中率(Hit Ratio)记为 :
越接近于1 性能越好
称为缺失率(Miss Ratio)。命中情况下的访问时间记为 ,数据确实情况下的访问时间记为 ,
cache/主存系统的平均访问时间记为 :
越接近于1, 越接近
访问效率记为 :
越接近于1, 越接近1
一般为5~10,不能太大
4.6.2 Cache 读、写流程
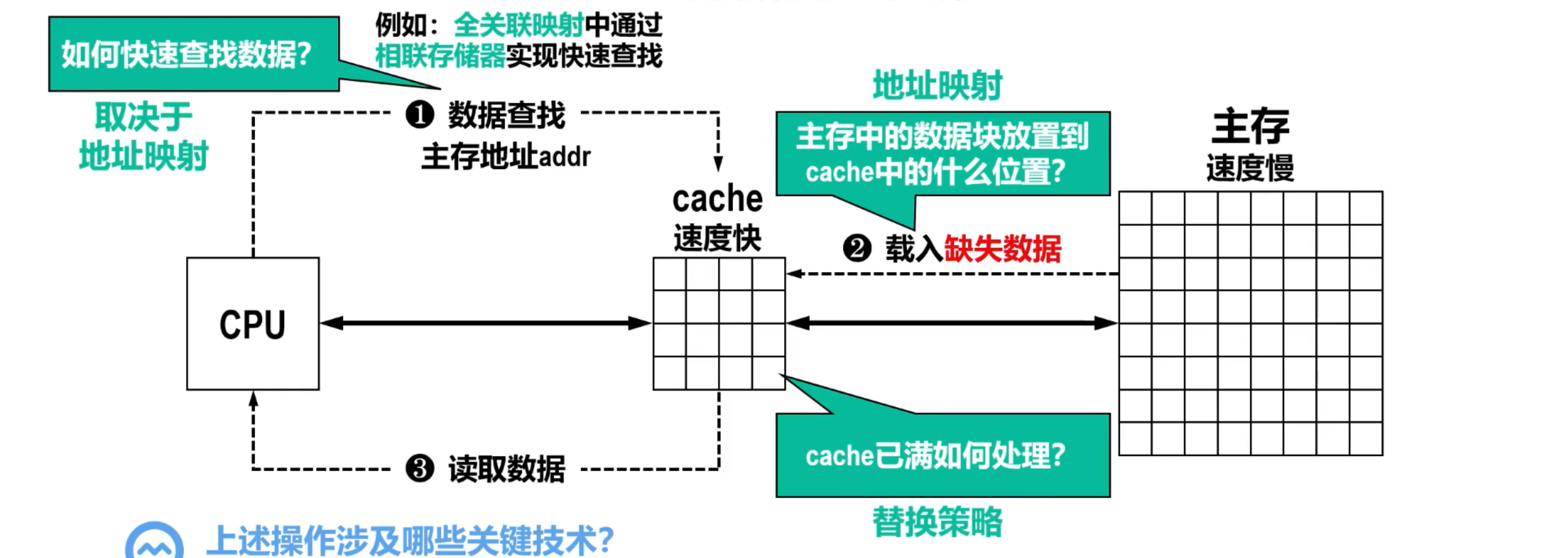
读操作
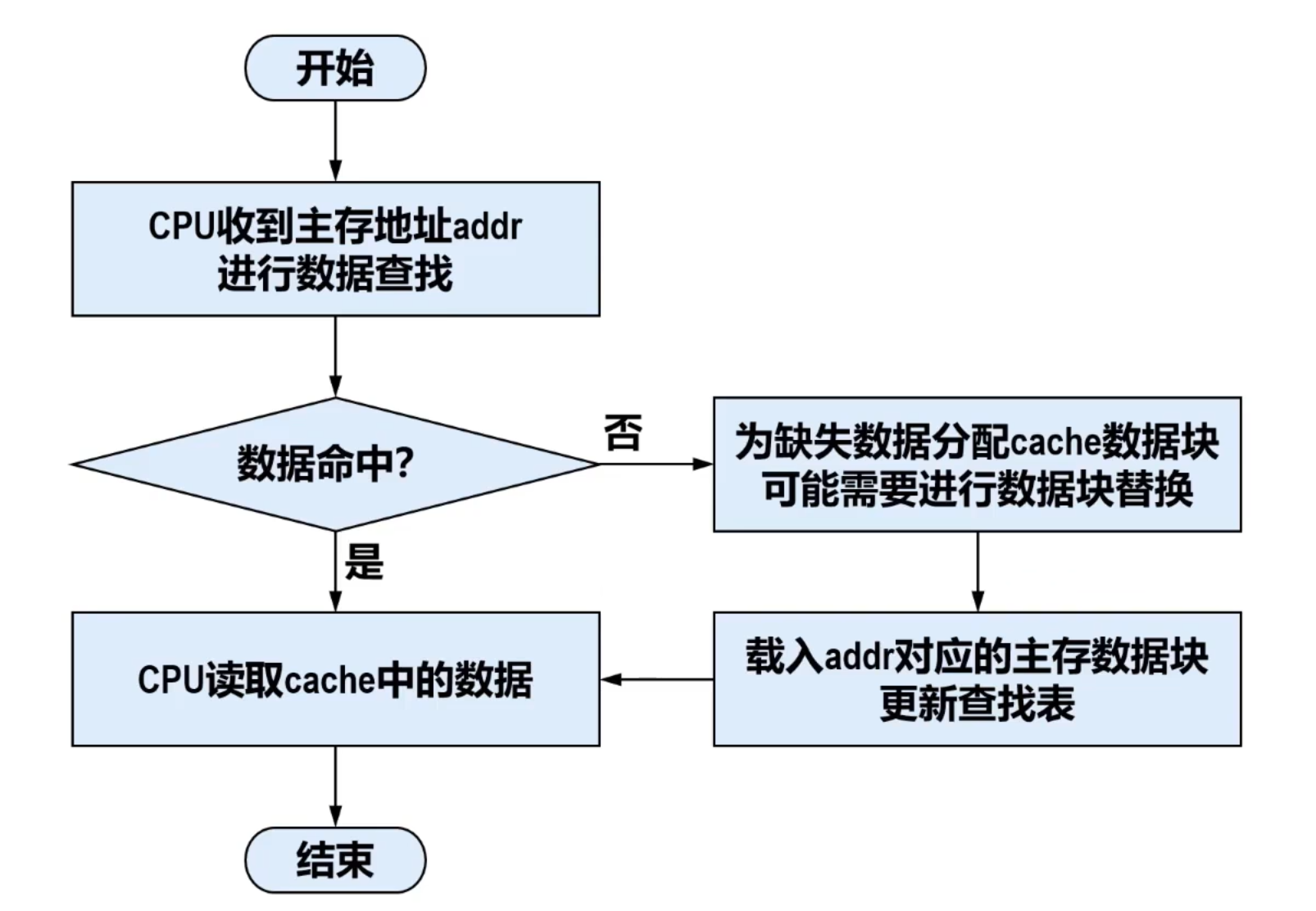
- 若是数据命中,则访问时间较快,数据缺失则访问时间较慢
- 构建cache系统时,应尽可能提高命中率,以提升读操作性能。
- 通过较好的替换策略,将经常访问的热数据保留在cache中,将不经常访问的冷数据淘汰,来充分利用时间局部性,以提高命中率。
- 数据缺失时,会将缺失数据所在数据块中的其他数据一起载入,这种预读策略可以充分利用空间局部性来提高顺序访问的命中率。
写操作
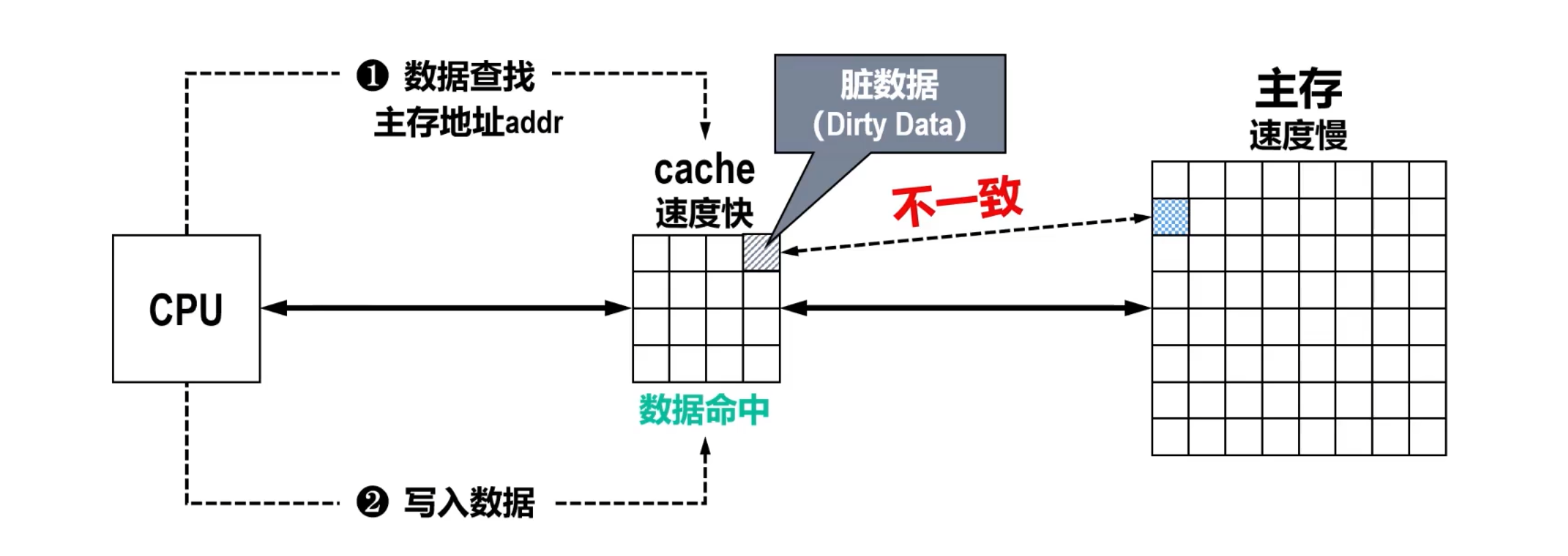
- 写回(Write-back)策略 此时写入操作结束,这种方式响应速度最快,但会产生不一致性。
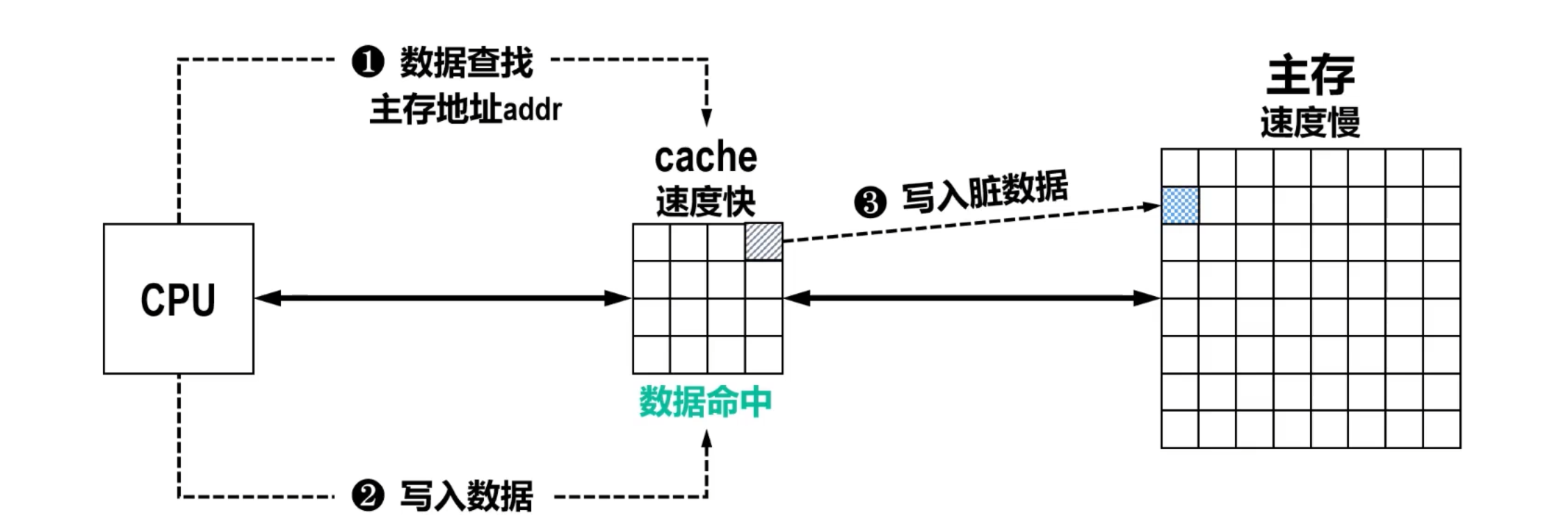
- 写穿(Write-through)策略 此时还需要将脏数据写入慢速的主存中才能结束,这种方式响应速度较慢,但没有脏数据产生。
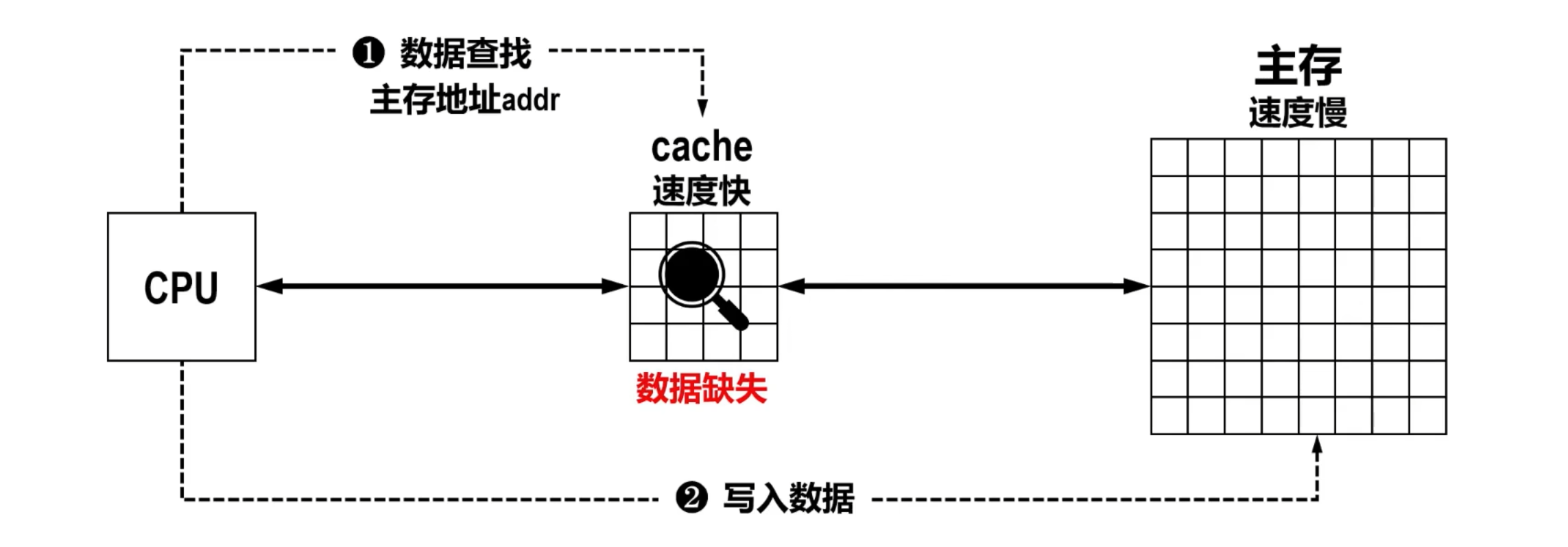
- 非写分配策略 此时将数据写入慢速主存即可返回。
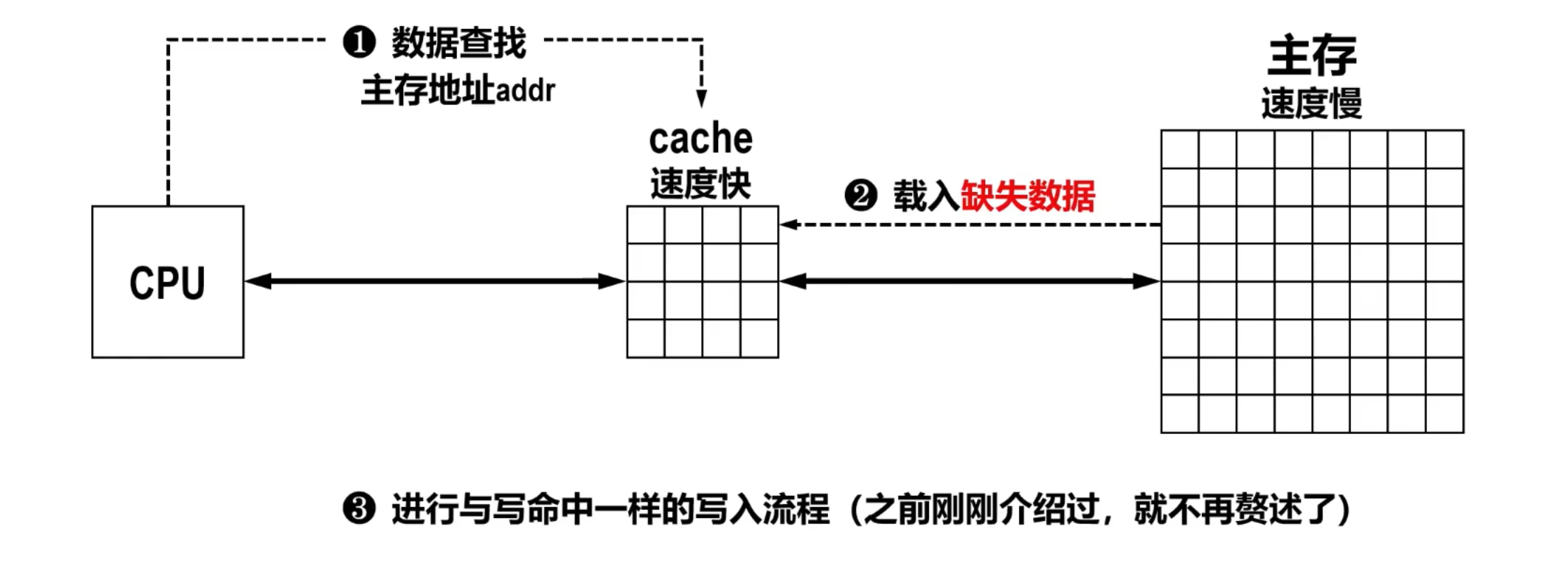
- 写分配(Write-Allocate)策略
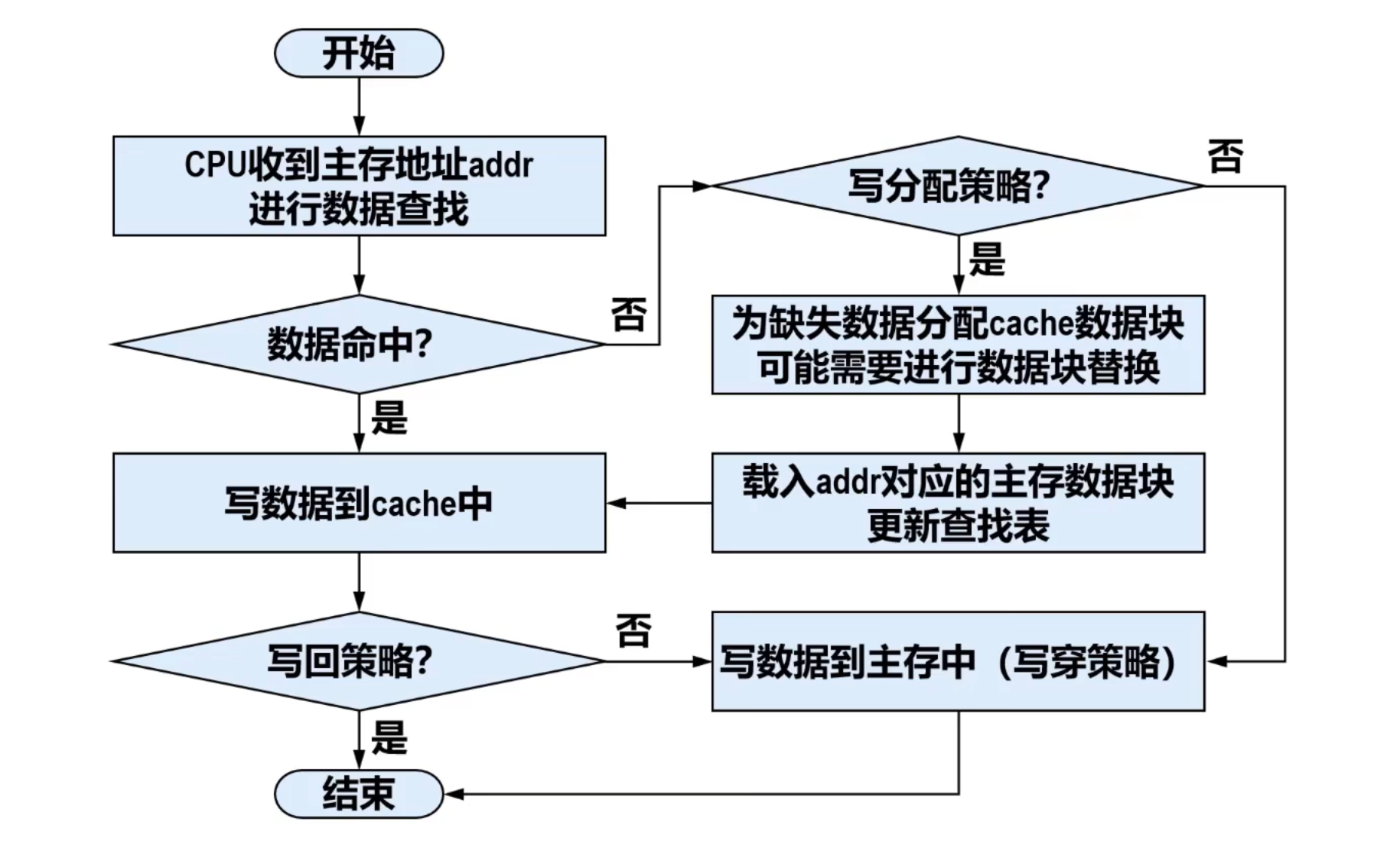
- 采用写回策略时,将数据写入cache即可返回,写响应时间最短。
- 对于突发的小数据量写入,cache能明显提高写入性能。
- 然而,由于cache容量很小,当cache写满数据后,需要将cache中的脏数据淘汰,这就需要先将脏数据迁移到主存中,然后从主存载入新数据块到cache后才能向cache写入新数据,该过程的写性能比没有采用cache的主存还要慢。
4.6.3 Cache 映射
本节内容整理自B站up主"小狗走两步"的视频帮你把Cache映射梳理清楚! | 图解cache映射_哔哩哔哩_bilibili
-
每串数据都有相应的一个地址,也就是根据某个地址,可以在主存中找到相应位置的数据
-
地址的长度,需通过计算机的编址方式得到。比如是"按字节编址",数据就每8bit便分配一个地址(64位架构下)
-
或者再通过存储器的容量,来知道地址的个数。比如容量为4MB的主存, 按2B编址则为 个地址
映射地址结构
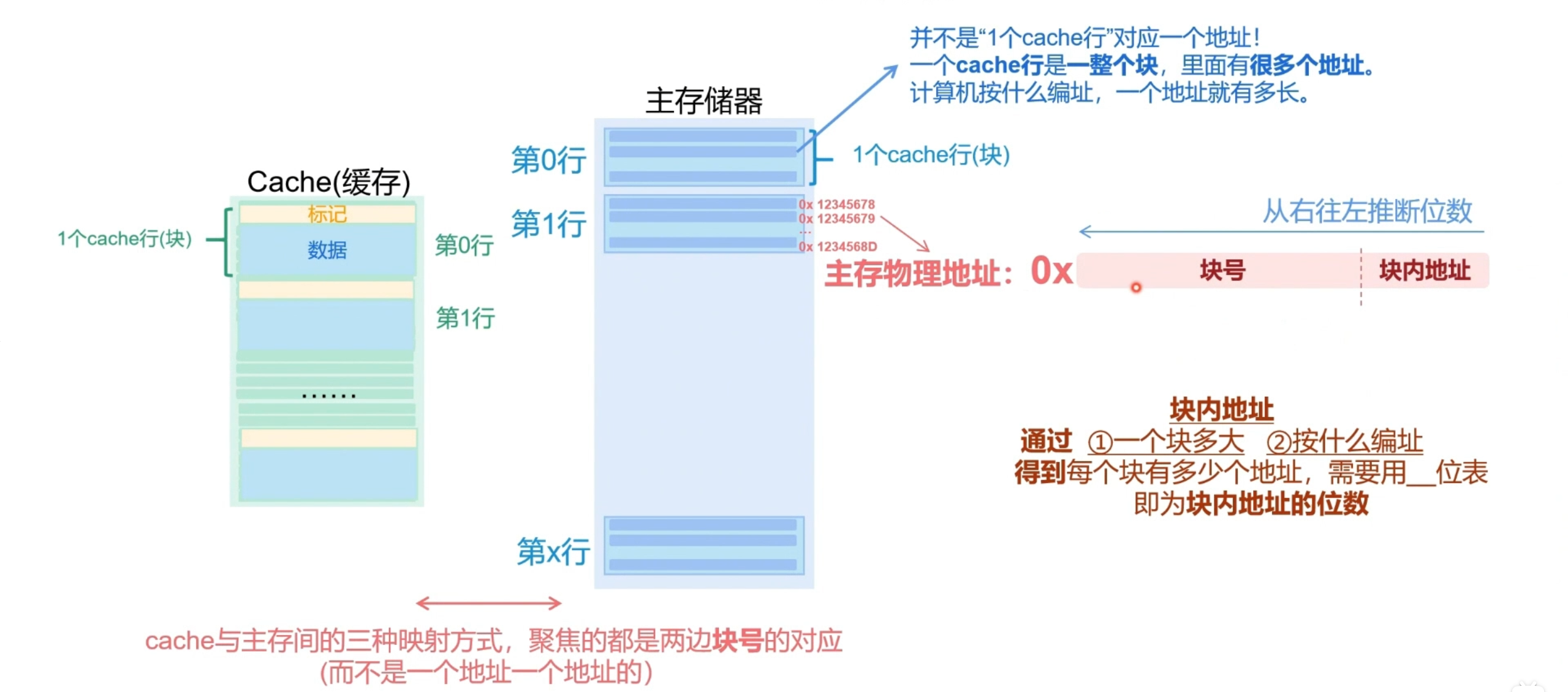
- cache与主存间的映射,是基于两边块号的对应,而并非每个单独地址的对应
- 在cache内部,1个cache行其实是一个块,里面有多个地址,主存中的数据也是同样道理,而其中地址的排序是一定的,若已知某个地址在主存中某一行的第几个,就能知道cache里对应的行里该地址的位置
- 主存中的物理地址是以 0x 块号|块内地址 的形式存储,低位是块内地址,高位是块号
- 分块的过程可理解为取模的过程,例如某主存每一个块能容纳32个地址,每个地址64位,则先用某地址的数对32取模,余数放在低位即块内地址,商放在高位即块号。 因此需要5bit来表示块内地址,剩下的59bit可用来表示块号,即整个主存可分为 个cache块
映射方式
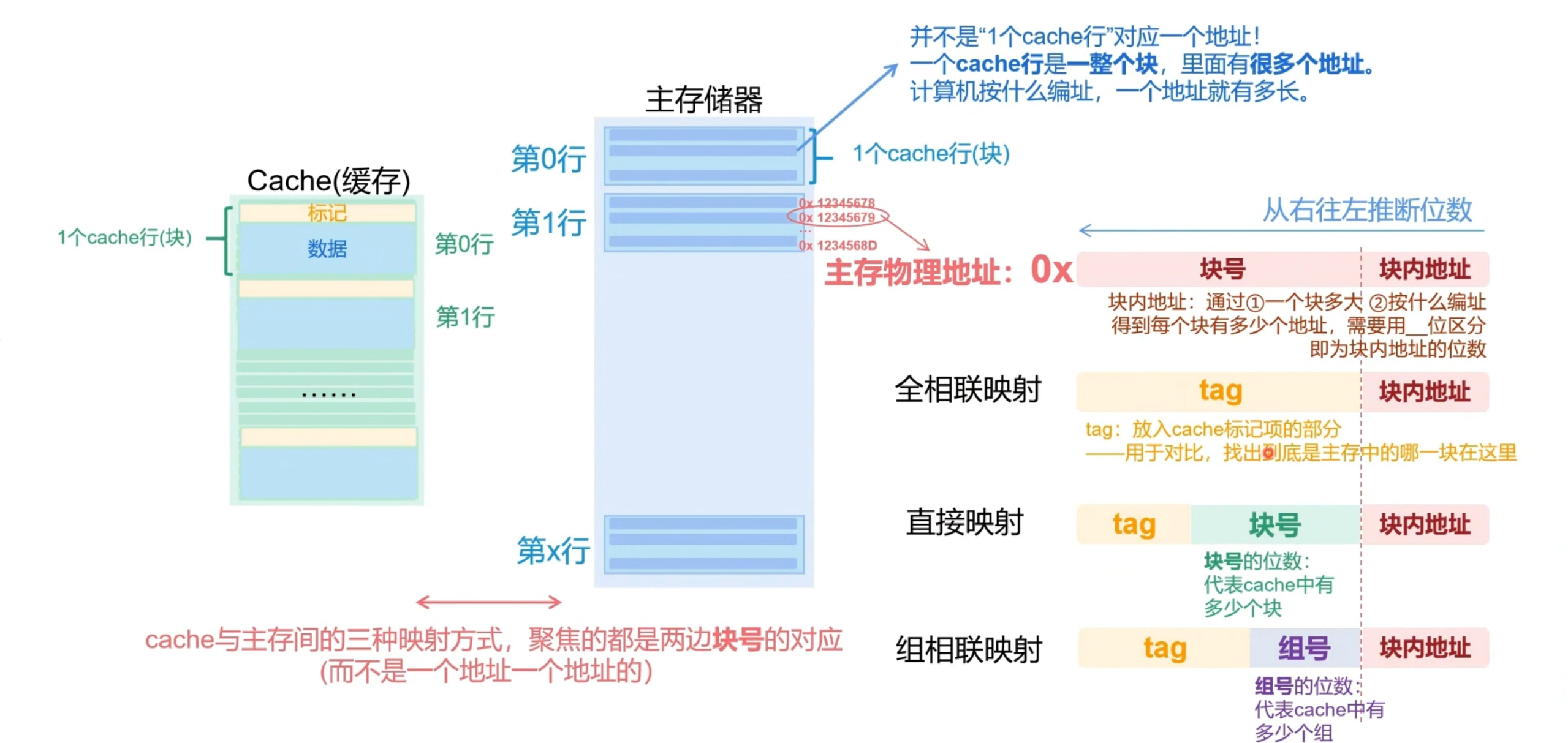
全相联映射
- 在cache中随机选取任一空的位置存储主存中的块
- 用块号作为cache块的标记(tag),用于对比和找出到底是主存的哪一块在这里,所以每次查找就需要遍历整个cache,时间开销较大
直接映射
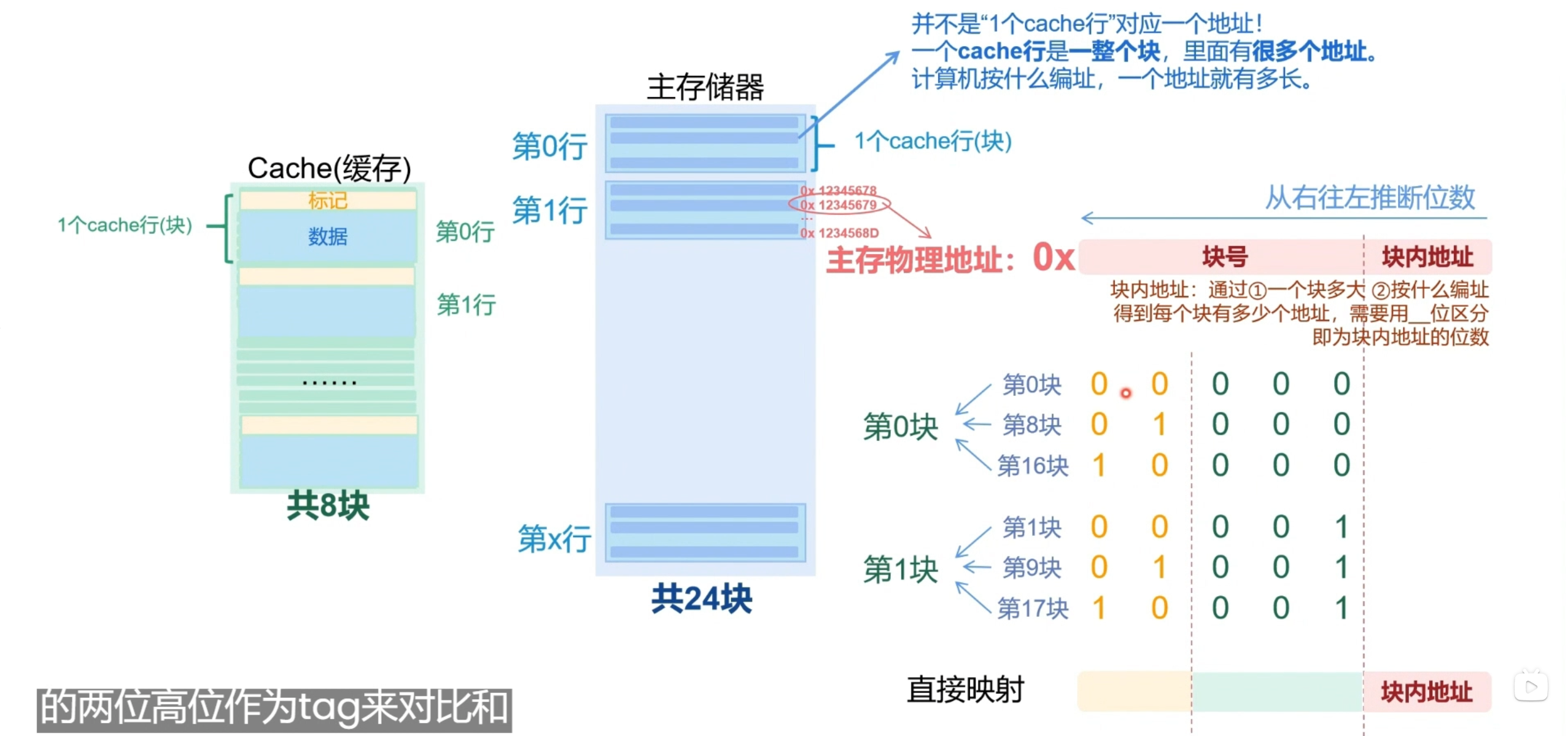
- 先确定cache的容量和主存的容量,即有多少个块,用主存的块号来对cache的容量块数取模,和上面分块的过程类似
- 例如上图的例子,块号的低位(低3位)表示在cache中的块号,高位(高2位)确认该cache块是否为所对应需要的主存中的地址
- 每个cache块的内容会不断的替换,如上图cache的第0块,需要不断的在主存第0块、第8块、第16块间替换,空间的利用不足
组相联映射
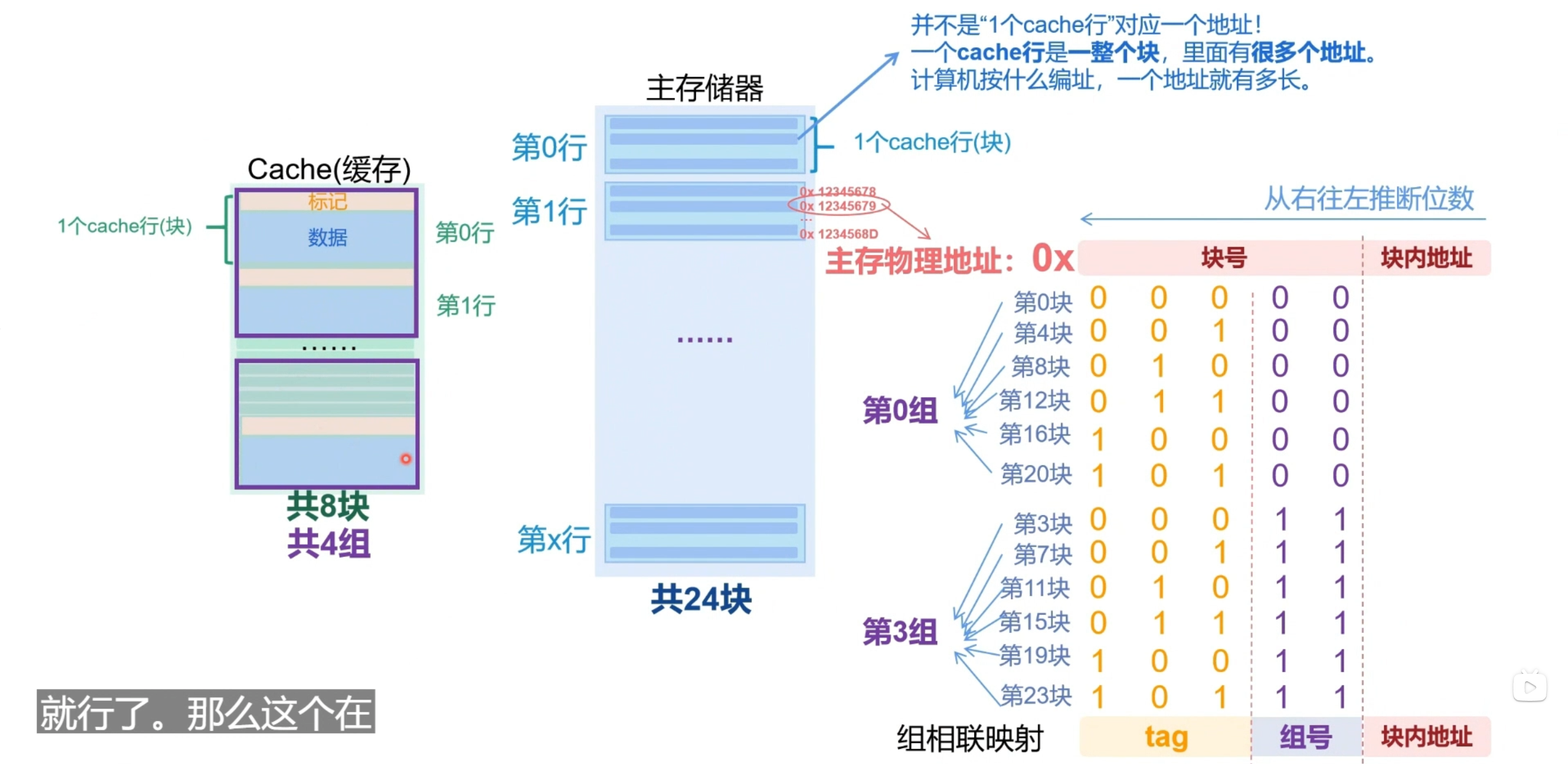
- 全相联映射和直接映射的结合,对cache进行分组
- 在总体上采用直接映射的方式,用取模后的低位数来分配具体的组号
- 在每个组内采用全相联映射的方法,即组内是随机挑选空位的,查找时只需要在组中遍历
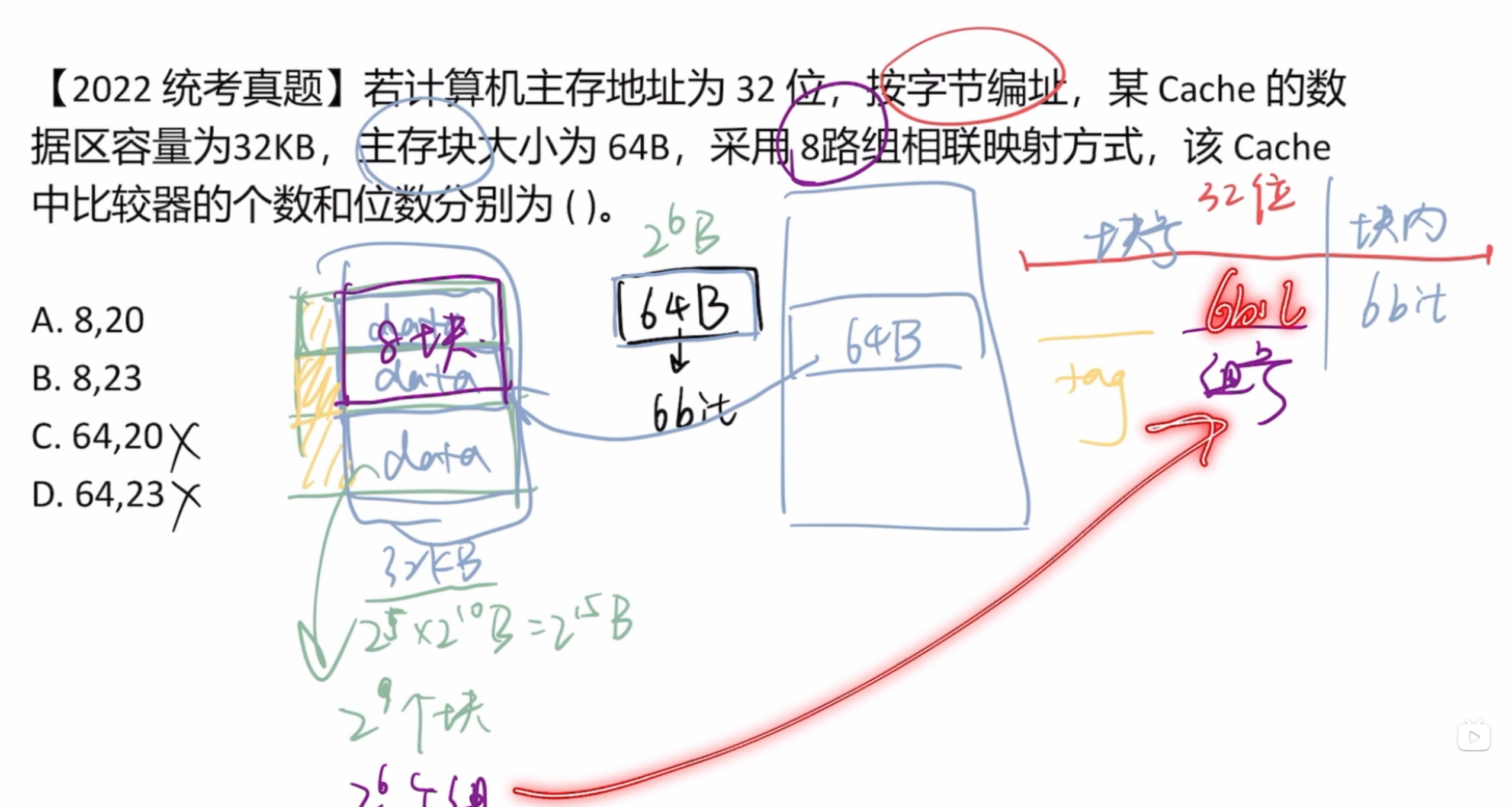
4.6.4 Cache 习题课
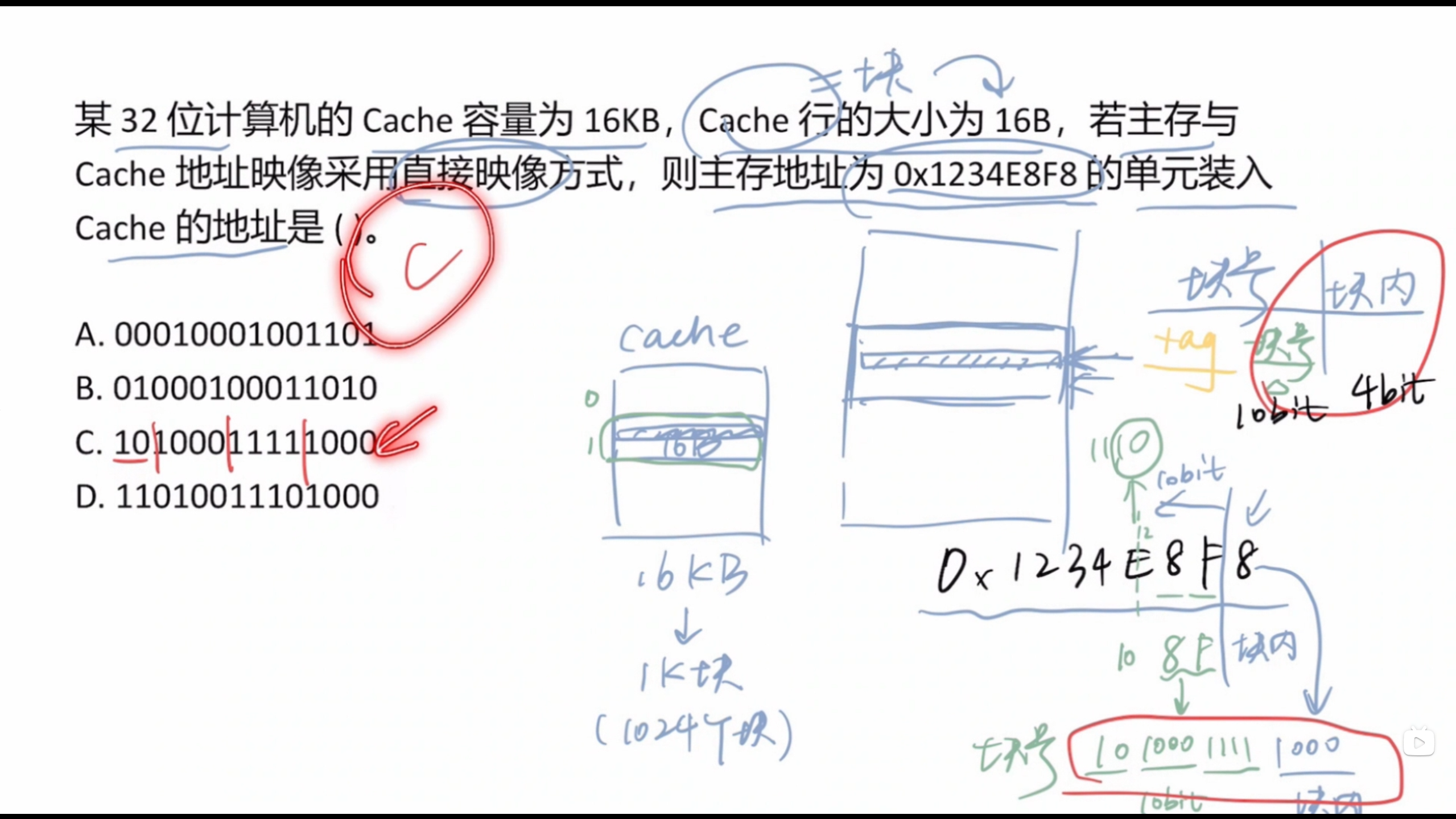
首先明确题目目标是要求出tag之后的块号+块内地址的部分
通过选项可以看出块号+块内地址的大小为14bit(14位)
再已知cache的容量得出的cache块数量为 个,块号部分大小为10位,则块内地址为 位
最后将十六进制的主存地址转化为二进制,取最后的14位
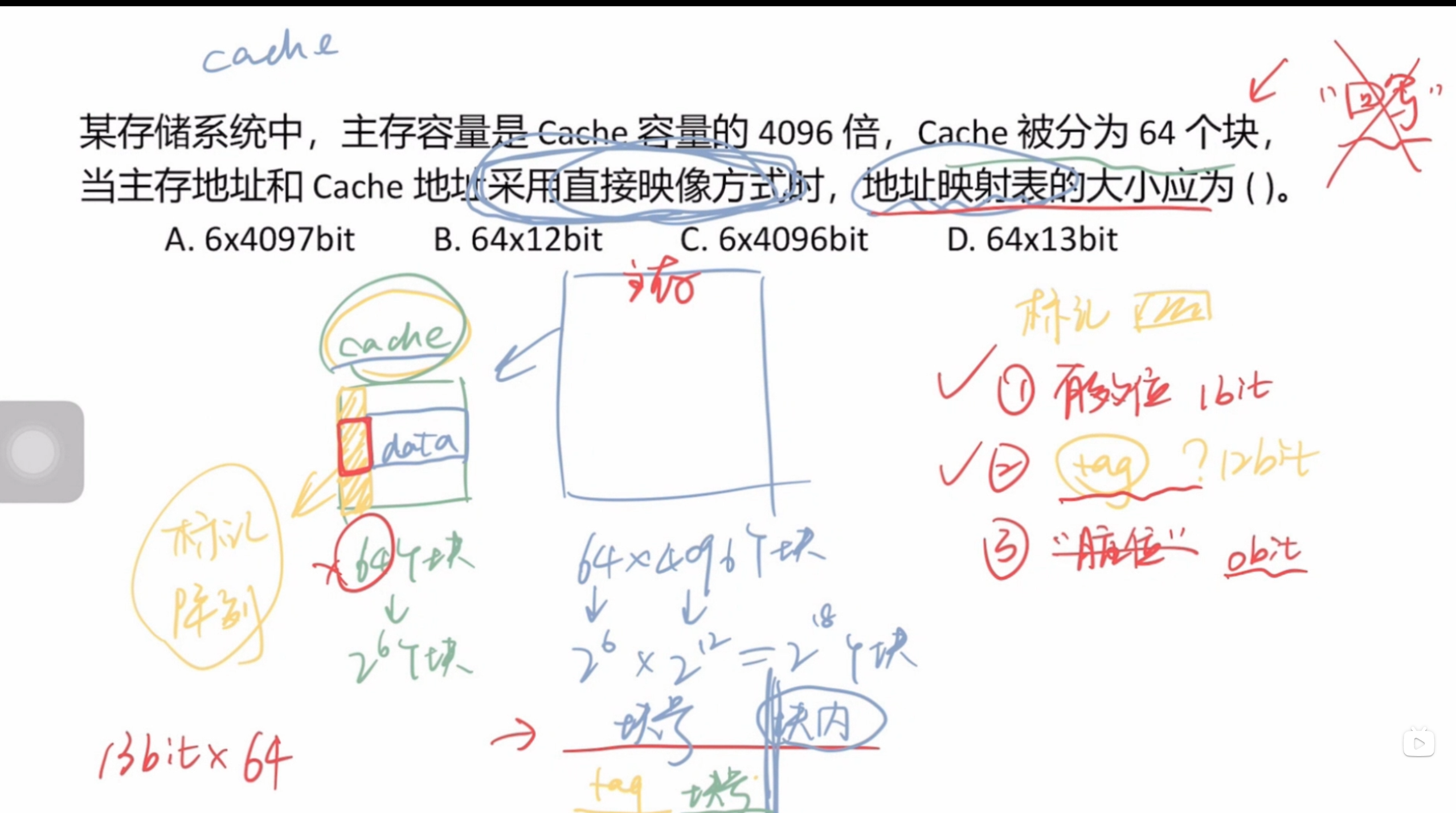
"地址映射表"即cache的“标记阵列”,也就是所有标记部分的总和,也就明确了本题先要求出标记位的长度
cache标记位简单地讲由有效位+脏位+tag组成,其中有效位占1bit,脏位通过观察题目中是否由“回写”判断,那本题没有,接下来的目标就是求出tag部分的长度
cache有 个块,cache块号部分就长6bit,主存容量为 个块,则主存块号长18bit,tag部分就长 bit,再加上有效位的1bit长
最终就是 bit
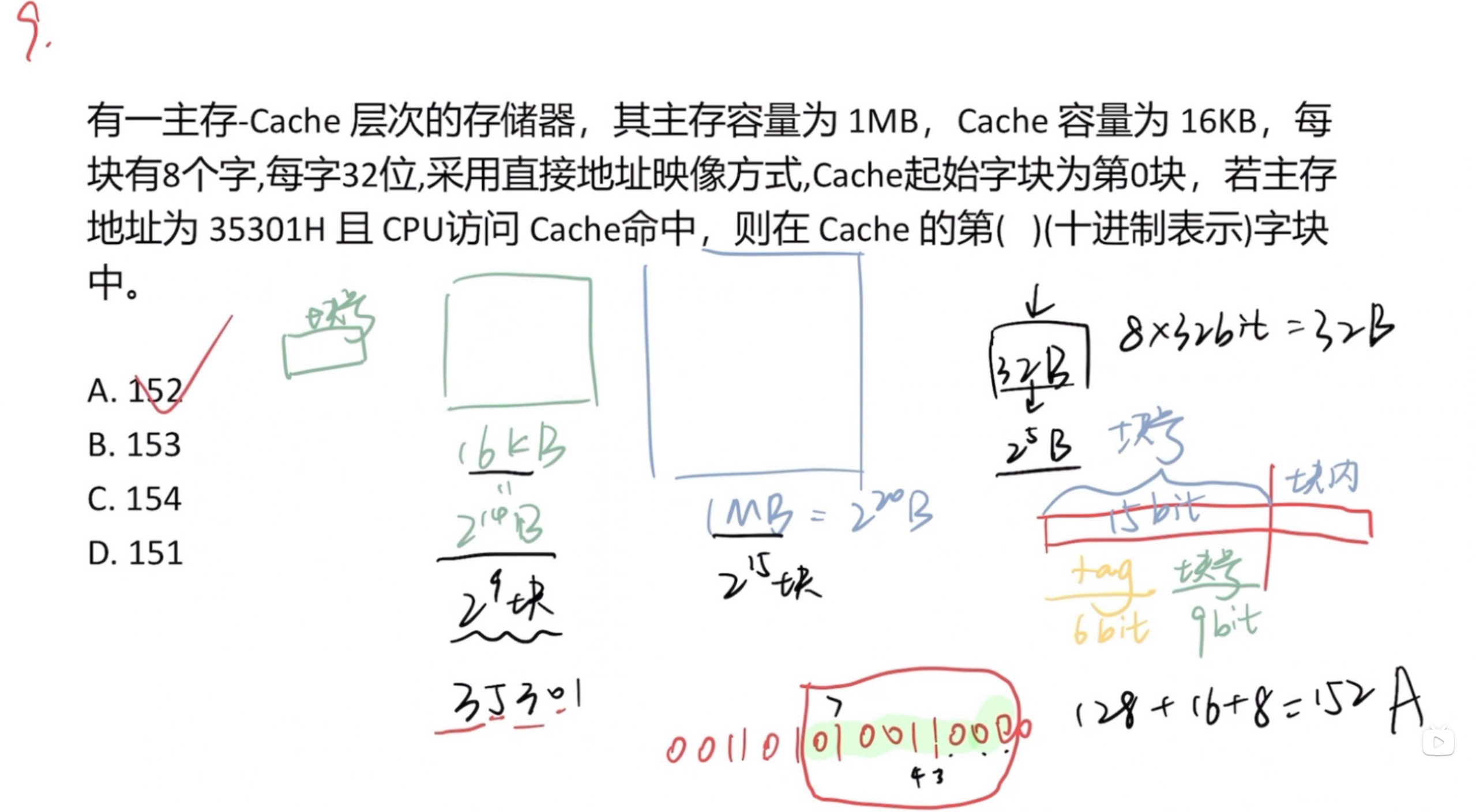
先得出每个块占用的空间为
cache容量除以每个cache块的空间得出cache块数量
同理,主存中块数量为
综上得出主存块号15位,cache块号9位,接下来将题目中给出的主存地址转为二进制并取前15位的后九位,即在 中取
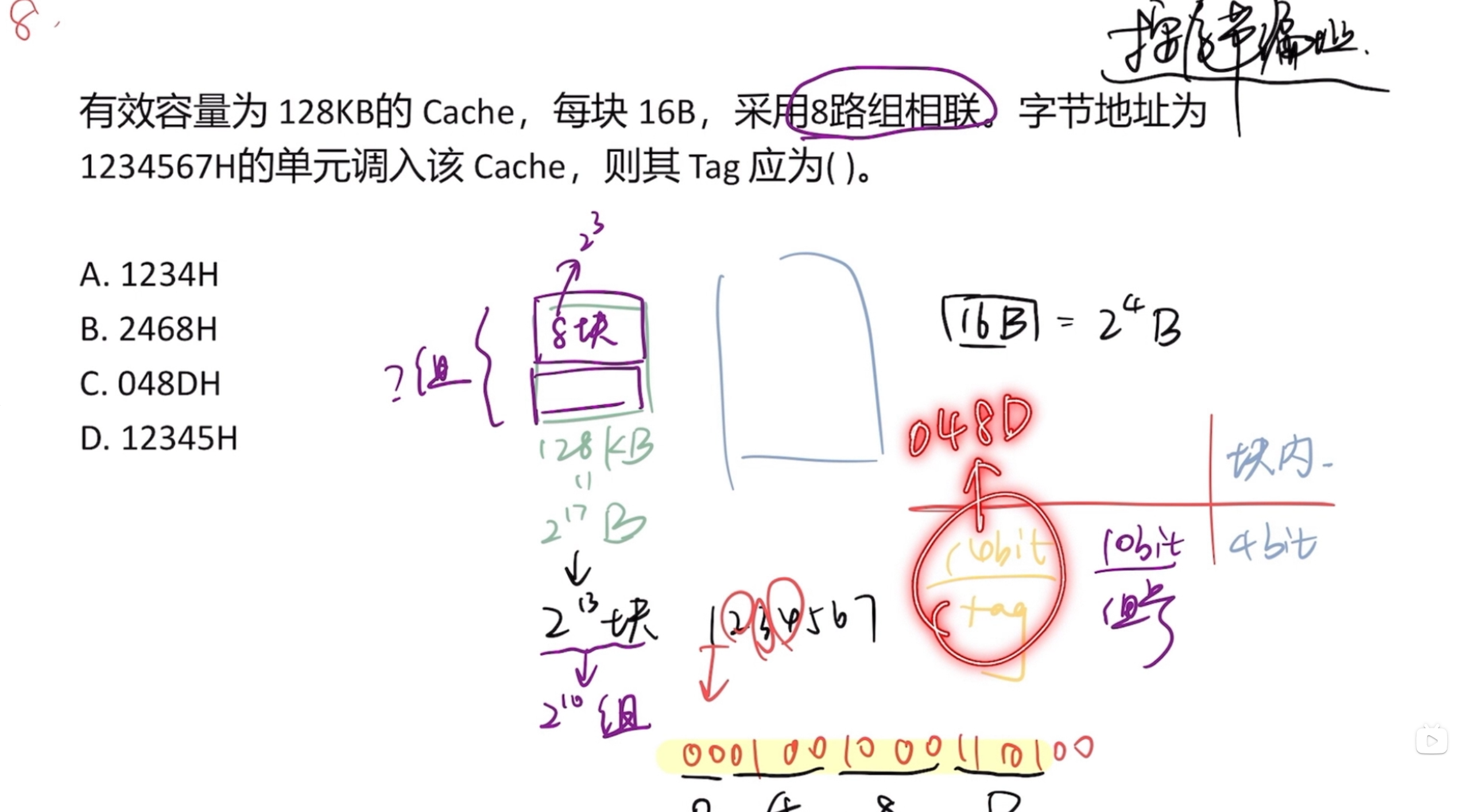
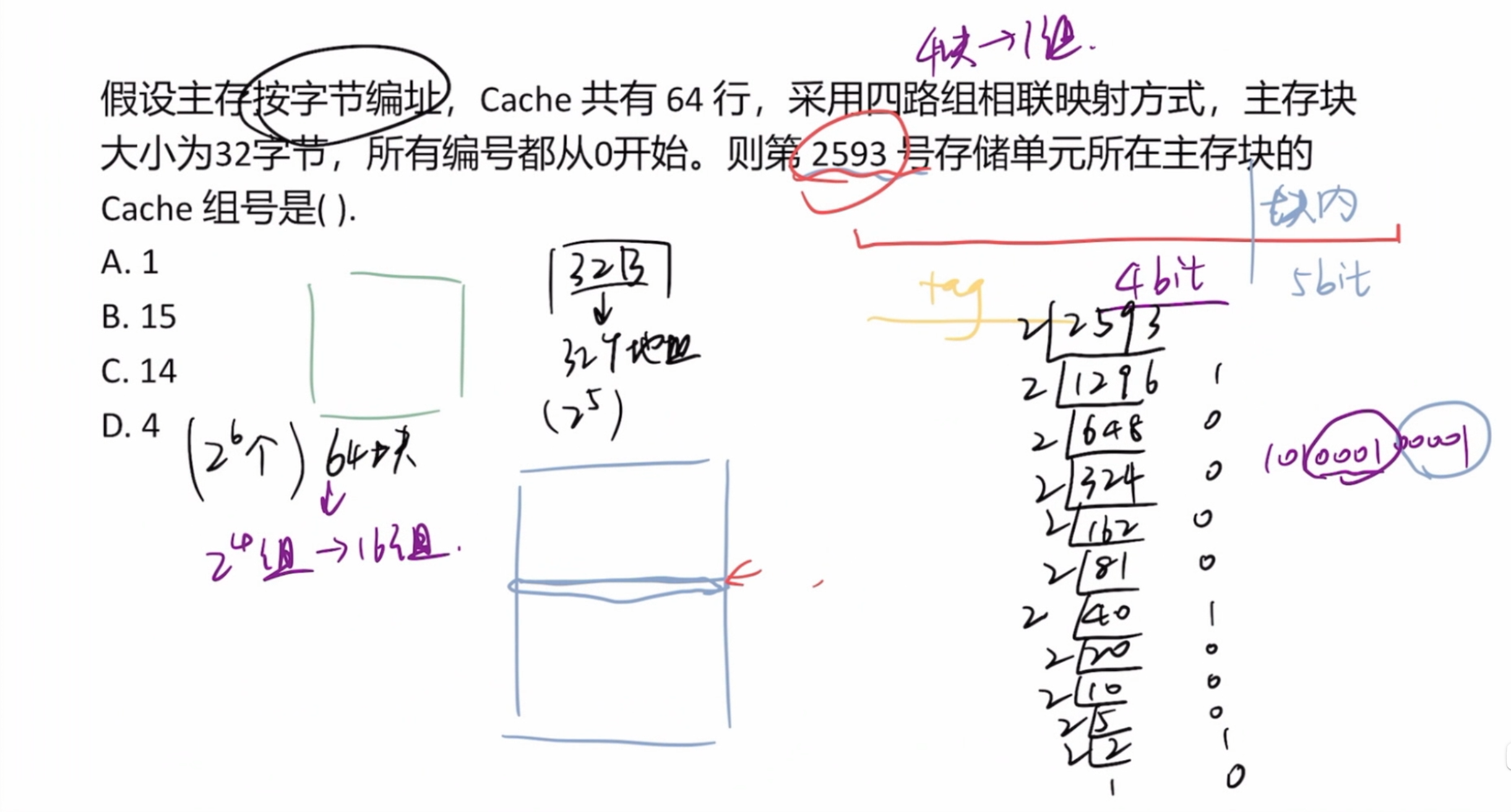
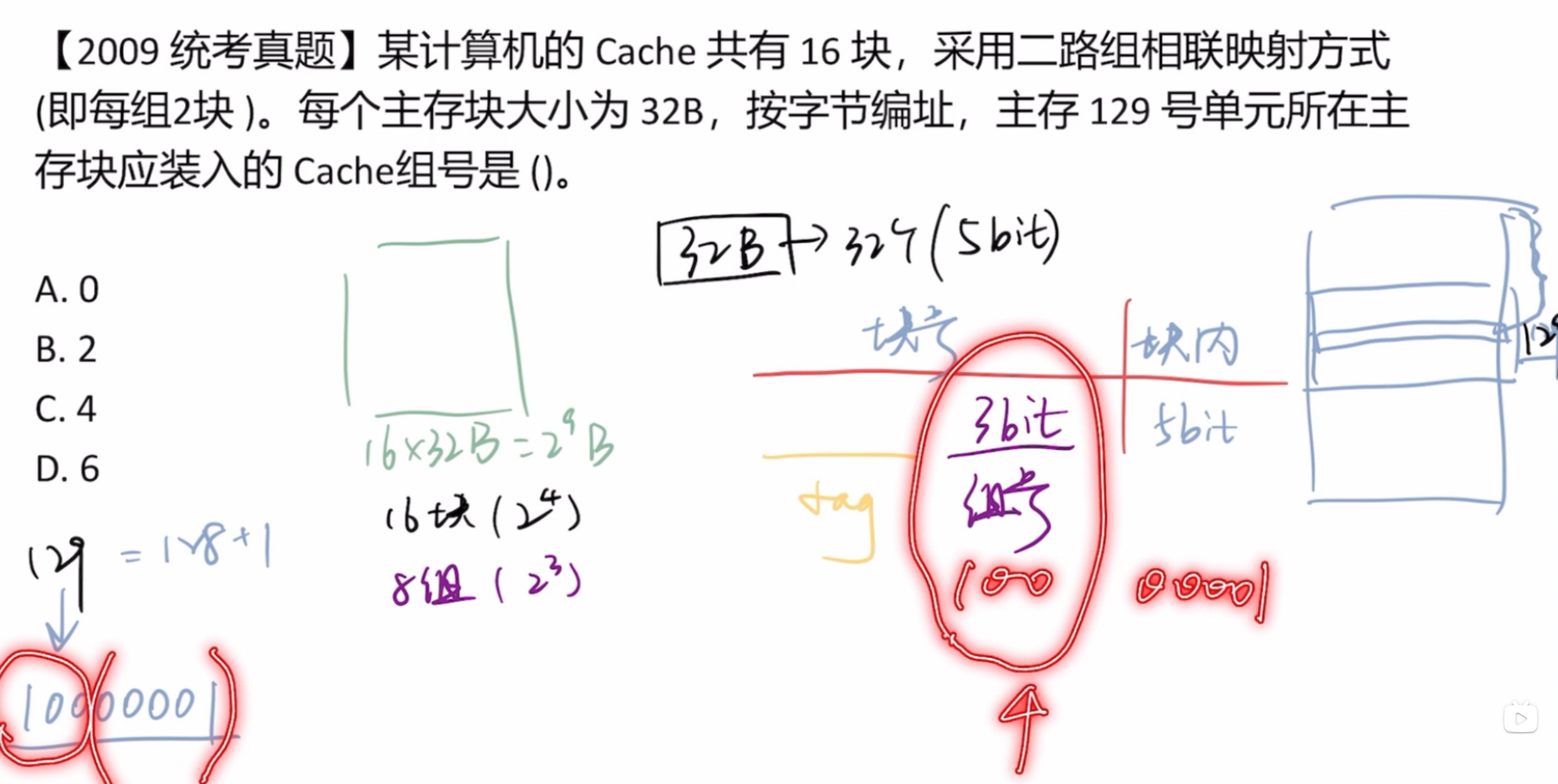
本题为“组相联映射”,基本思路和前面差不多,但地址的组成有变化,组相联需要在知道块数的情况下得出组数,本题 也就知道了组号为10bit长,块内地址由“每块16B”可知,长4bit
地址的位数由题目的 可以看出有7位十六进制数,即28位二进制数,地址也就长28位
tag的长度应为 则取二进制的 的前14位即可
5.1.1 指令格式
本节内容整理自B站up主"王道计算机教育"的视频4.1.1+2+3_指令的基本格式_哔哩哔哩_bilibili
- 指令是指示计算机执行某种操作的命令,是计算机运行的最小功能单位。一台计算机的所有指令的集合构成该机的指令系统,也称为指令集。
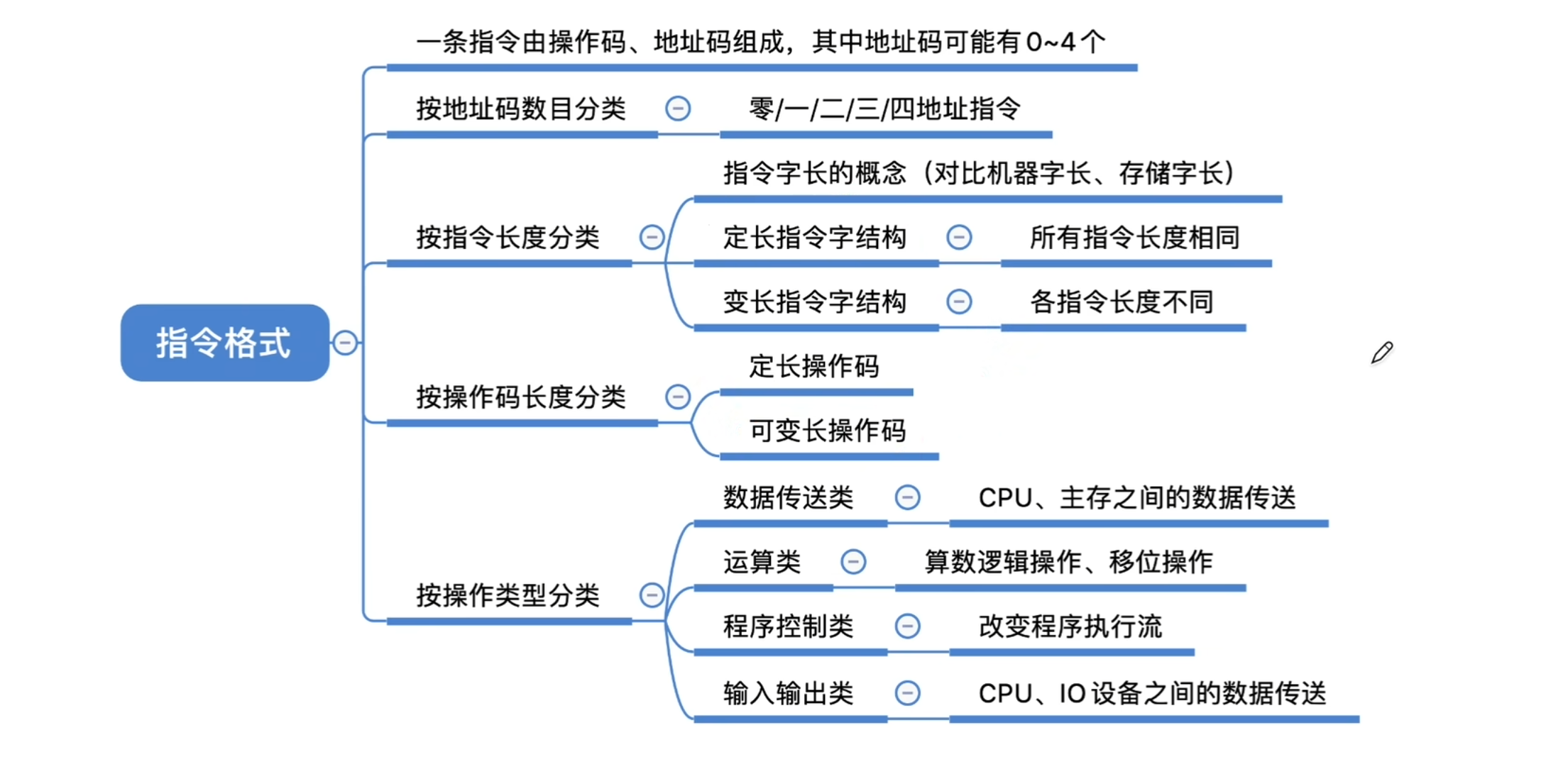
按操作数(地址码)分类
- 指令由操作码和地址码组成,一条指令包含的地址码数量不同。
- 零地址指令
- 不需要操作数,比如空操作、停机、关中断等。或者堆栈计算机,操作数隐含存放。
- 一地址指令
- 如只需要单操作数 完成一次需要三次访存:取指->读->写
- 或需要两个操作数的,但其中一个操作数隐含在某个寄存器 完成一次需要两次访存:取指->读
- 指某个主存地址,()表示 所指向的地址中的内容。
- 二地址指令
- 常用于需要两个操作数的算术运算、逻辑运算相关指令
- 完成一次需要访存4次,取指->读->读->写
- 三地址指令
- 常用于需要两个操作数的算术运算、逻辑运算相关指令
- 完成一次需要访存4次,取指->读->读->写
- 四地址指令
- 完成一次需要访存4次,取指->读->读->写
- 但与正常情况下,取指令后PC+1指向下一条指令不同,而是在执行指令后,将PC的值修改为所指的地址
- 零地址指令
按指令长度分类
- 指令字长:一条指令的总长度(可能会变)
- 机器字长:CPU进行一次整数运算所能处理的二进制数据的位数(通常和ALU直接相关)
- 存储字长:一个存储单元中的二进制代码位数(通常和MDR位数相同)
- 半字长指令、单字长指令、双字长指令——指令长度是机器字长的多少倍,指令字长会影响取指令所需时间。如:机器字长=存储字长=16bit,则取一条双字长指令需要两次访存
- 定长指令字结构:指令系统中所有指令的长度都相等
- 变长指令字结构:指令系统中各种指令的长度不等
按操作码长度分类
- 定长操作码:指令系统中所有指令的操作码长度都相同
- n位 -> 条指令
- 控制器的译码电路设计简单,但灵活性较低
- 可变长操作码:指令系统中各指令的操作码长度可变
- 控制器的译码电路设计复杂,但灵活性较高
- 定长指令字结构+可变长操作码 -> 扩展操作码指令格式
按操作类型分类
-
数据传送
-
进行主存与CPU间的数据传送
-
LOAD 作用:把存储器中的数据放到寄存器中
-
STORE 作用:把寄存器中的数据放到存储器中
-
-
算术逻辑操作
- 算术:加、减、乘、除、增1、减1、求补、浮点运算、十进制运算
- 逻辑:与、或、非、异或、位操作、位测试、位清除、位求反
-
移位操作
- 算术移位、逻辑移位、循环移位(带进位和不带进位)
-
转移操作
-
改变程序执行的顺序
-
无条件转移 JMP
-
条件转移 JZ:结果为0;JO:结果溢出;JC:结果有进位
-
调用和返回 CALL和RETURN
-
陷阱(Trap)与陷阱指令
-
-
输入输出操作
- 进行CPU与I/O设备之间的数据传送
5.1.2 扩展操作码指令格式
-
定长指令字结构+可变长操作码->扩展操作码指令格式
-
不同地址数的指令使用不同长度的操作码
-
在设计扩展操作码指令格式时,必须注意以下两点:
- 不允许短码是长码的前缀,即短操作码不能与长操作码的前面部分的代码相同。
- 各指令的操作码一定不能重复。
-
通常情况下,对使用频率较高的指令,分配较短的操作码;对使用频率较低的指令,分配较长的操作码,从而尽可能减少指令译码和分析的时间。
扩展操作码举例
指令字长为16位,每个地址码占4位:
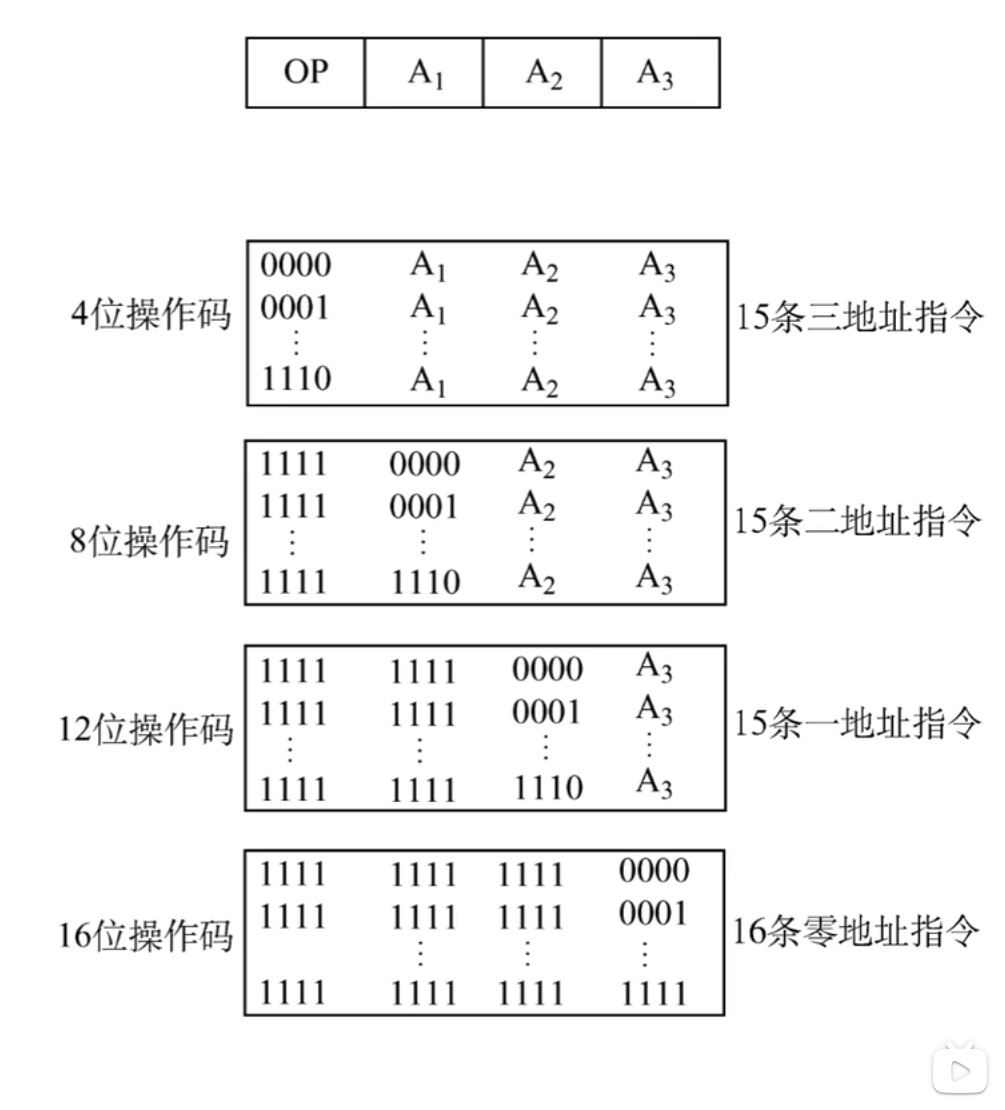
- 前4位为基本操作码字段OP,另有3个4位长的地址字段
4位基本操作码若全部用于三地址指令,则有16条。
- 但至少须将1111留作扩展操作码之用,即三地址指令为15条;
- 1111 1111留作扩展操作码之用,二地址指令为15条;
- 1111 1111 1111留作扩展操作码之用,一地址指令为15条;
- 零地址指令为16条。
再举例,设指令字长固定为16位,试设计一套指令系统满足:有15条三地址指令,有12条二地址指令,有62条一地址指令,有32条零地址指令
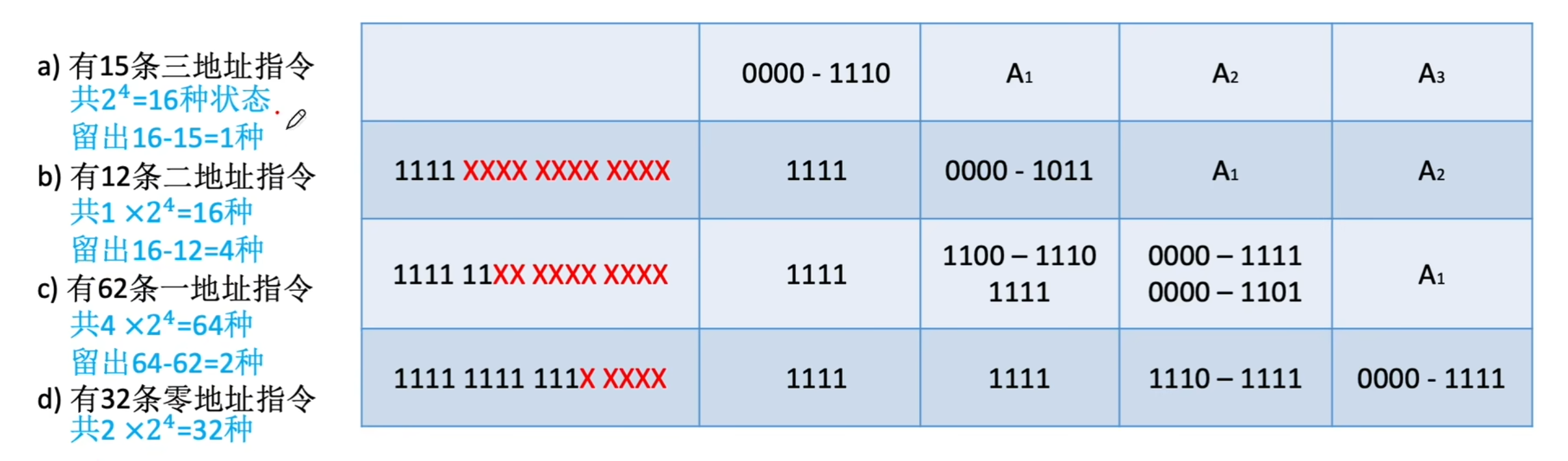
15条三地址指令,需最前面的四位是从0000~1110共15条,同上例,下个数就为1111
到12条二地址指令,前四位为1111,再四位是从0000~1011共12条,下个数为1100
由于二地址的设计,前六位为111111留作扩展操作码之用,62条一地址指令需用12位操作码的后六位来表示061即000000111101,下个数为111110
由于一地址的设计,前十一位为11111111111留作扩展操作码之用,32条零地址指令正好用剩余的五位来表示(零地址指令无需地址码)
- 设地址长度为n,上一层留出m种状态,下一层可扩展出 种状态
定长与不定长操作码的对比
扩展操作码(不定长操作码):
- 全部指令的操作码字段位数不固定,且分散地放在指令字的不同位置上。
- 最常见的变长操作码方法是扩展操作码,使操作码的长度随地址码的减少而增加,不同地址数的指令可以具有不同长度的操作码,从而在满足需要的前提下,有效地缩短指令字长。
- 优点:在指令字长有限的前提下仍保持比较丰富的指令种类。
- 缺点:增加了指令译码和分析的难度,使控制器的设计复杂化。
定长操作码:
- 在指令字的最高位部分分配固定的若干位(定长)表示操作码。
- 一般n位操作码字段的指令系统最大能够表示 条指令。
- 优点:定长操作码对于简化计算机硬件设计,提高指令译码和识别速度很有利。
- 缺点:指令数量增加时会占用更多固定位,留给表示操作数地址的位数受限。
5.2.1 指令寻址
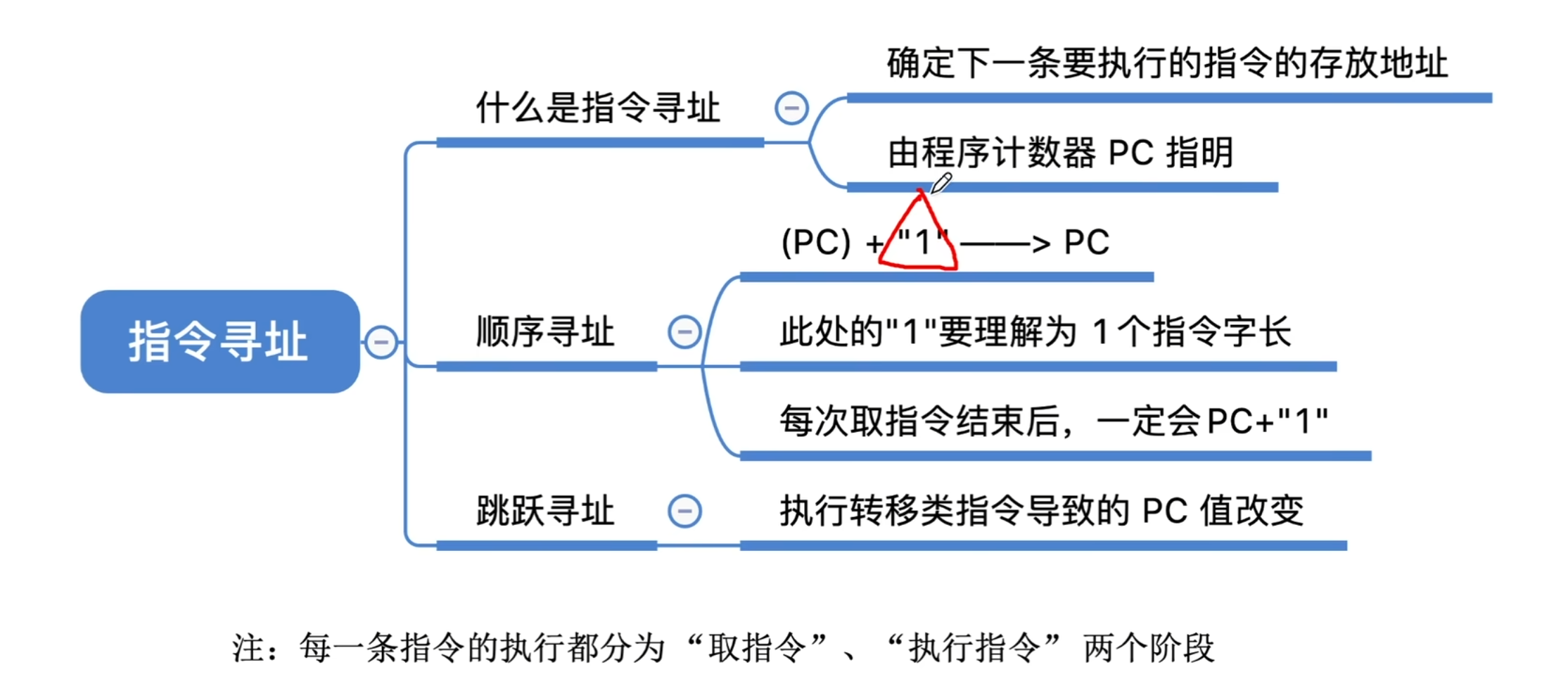
顺序寻址

- “主存按字节编址”说明每一条指令占两个地址
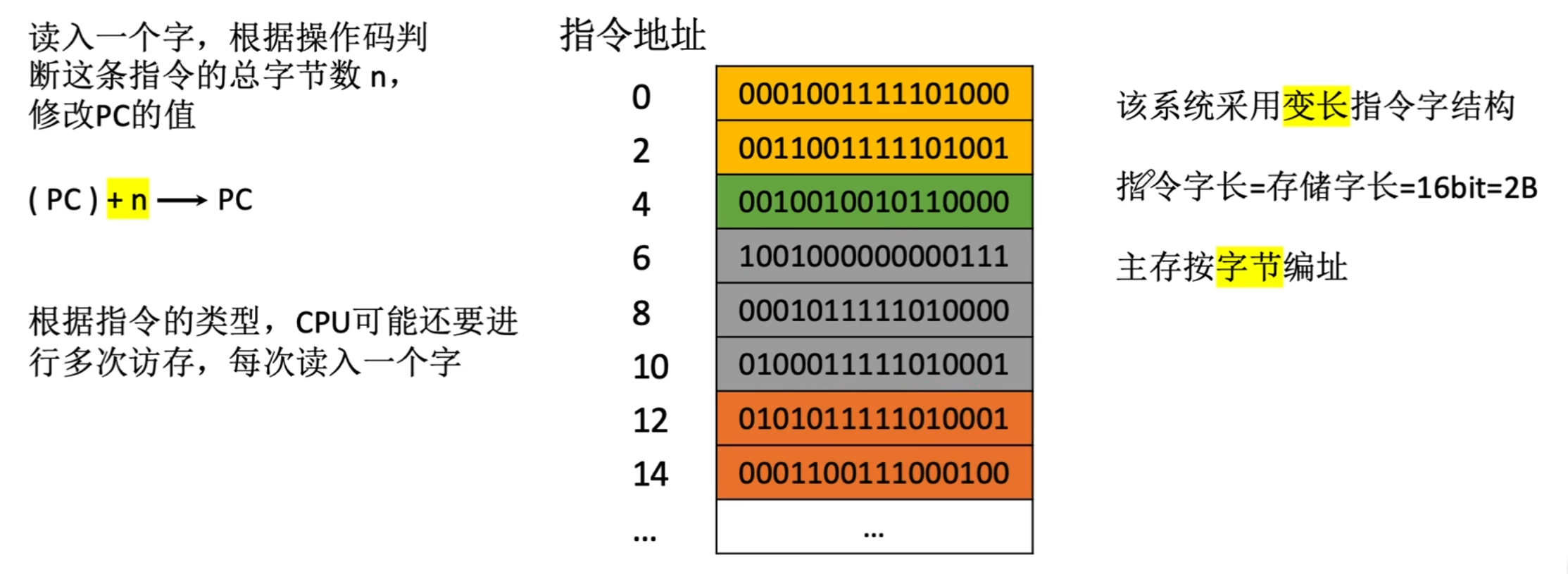
- “变长指令结构”下,各种指令占用的大小不同,PC的值根据读取命令的字长变化而非固定的变化,同时CPU读取一条指令可能要多次访存
- 这里的"1"理解为1个指令字长,实际加的值会因指令长度、编址方式而不同
跳跃寻址
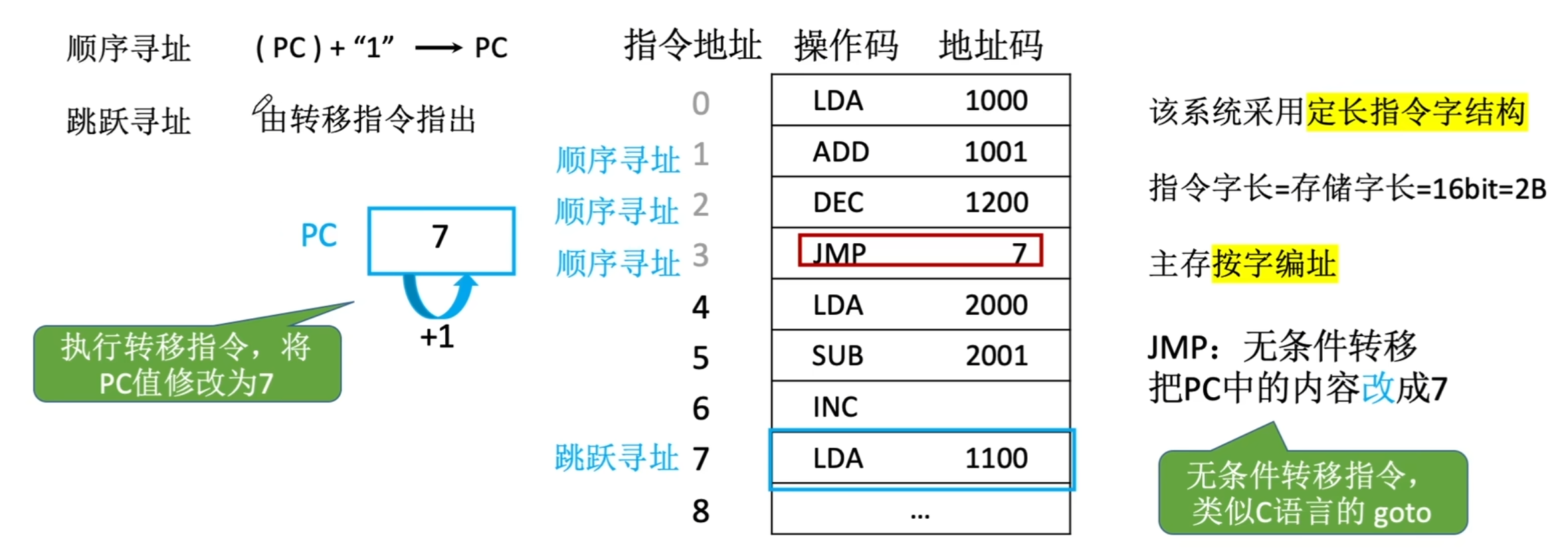
- 与顺序寻址不同,由转移指令,将PC的值直接进行修改而非顺序执行,便是跳跃寻址。以某个地址作为起点,形式地址视为“偏移量”。
5.2.2 偏移寻址
- 基址寻址:以程序的起始存放地址作为“起点”
- 变址寻址:程序员自己决定从哪里作为“起点”
- 相对寻址:以程序计数器PC所指地址作为“起点”
基址寻址
- 将CPU中基址寄存器(BR base address register)的内容加上指令格式中的形式地址A,而形成操作数的有效地址,即
- 但CPU中不一定有专用的基址寄存器,而都是通用寄存器,这时就需要在指令中指明哪个通用寄存器作为基址寄存器使用,要根据通用寄存器总数来判断要用几个bit来指明寄存器。
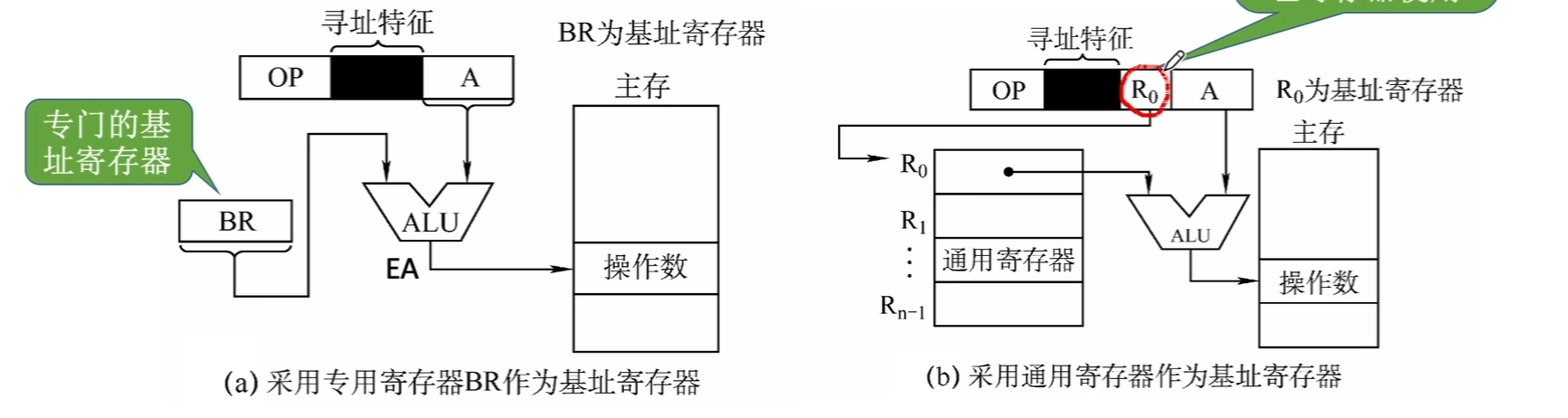
- 如图,BR的地址为程序开始存放的地址,即第一条指令的地址,“取数a至ACC”
- 地址码101即访问地址为5的数据a,但这里都是相对地址而非绝对地址
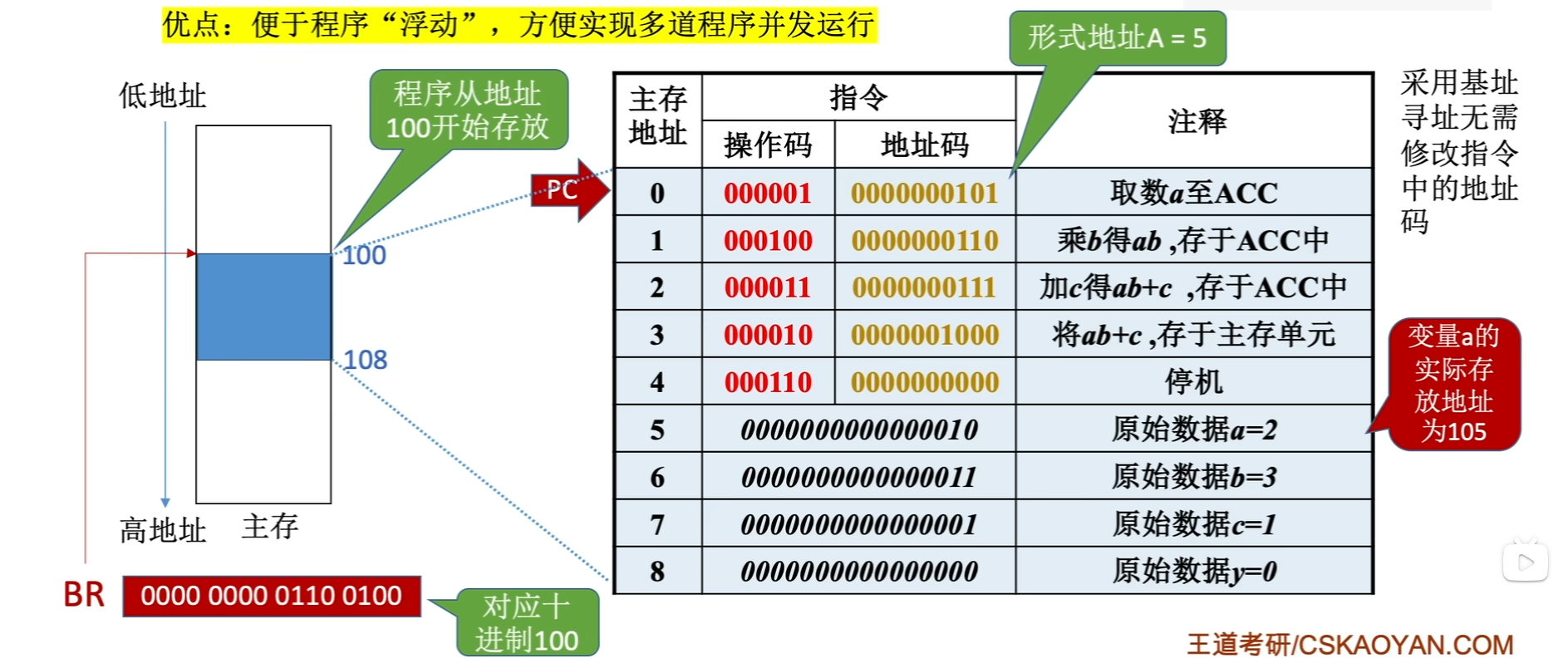
- 基址寄存器是面向操作系统的,其内容由操作系统或管理程序确定。在程序执行过程中,基址寄存器的内容不变(作为基地址),形式地址可变(作为偏移量)。
- 当采用通用寄存器作为基址寄存器时,可由用户决定哪个寄存器作为基址寄存器,但其内容仍由操作系统确定。
- 优点:可扩大寻址范围(基址寄存器的位数大于形式地址A的位数);用户不必考虑自己的程序存于主存的哪一空间区域,故有利于多道程序设计,以及可用于编制浮动程序(整个程序在内存里边的浮动)。
变址寻址
- 有效地址EA等于指令字中的形式地址A与变址寄存器(IX index register)的内容相加之和,即 ,其中IX可为变址寄存器(专用),也可用通用寄存器作为变址寄存器。
- 变址寄存器是面向用户的,在程序执行过程中,变址寄存器的内容可由用户改变(IX作为偏移量),形式地址A不变(作为基地址)。
- 如图中的循环累加案例,我们把数组起始的地址作为形式地址,IX看作偏移量,在地址3,4,5的指令,由用户对IX进行操作和比较,从而实现了数组的循环累加,直到IX的值达到数组的最大容量
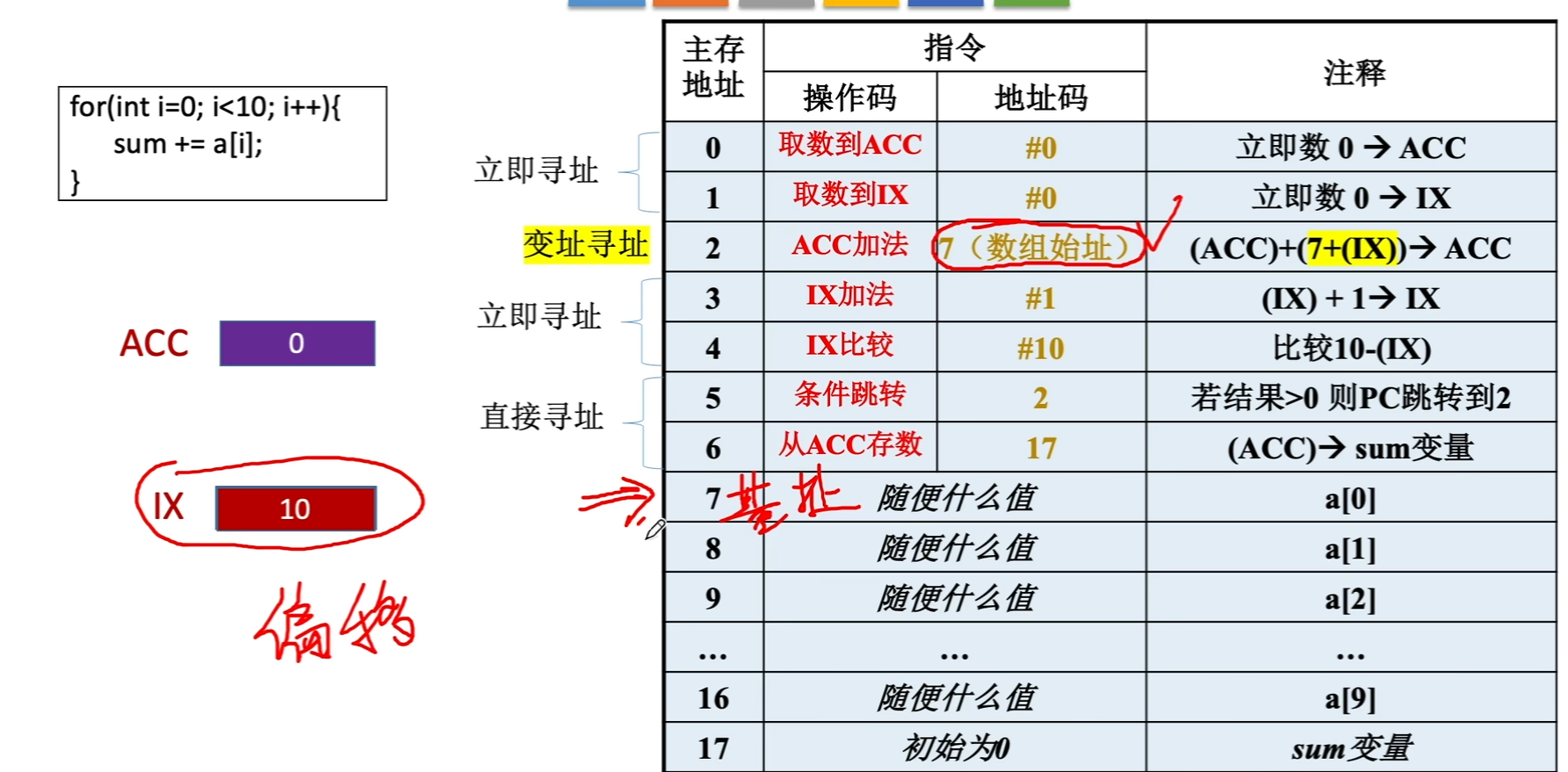
- 优点:在数组处理过程中,可设定A为数组的首地址,不断改变变址寄存器IX的内容,便可很容易形成数组中任一数据的地址,特别适合编制循环程序。
基址变址复合寻址
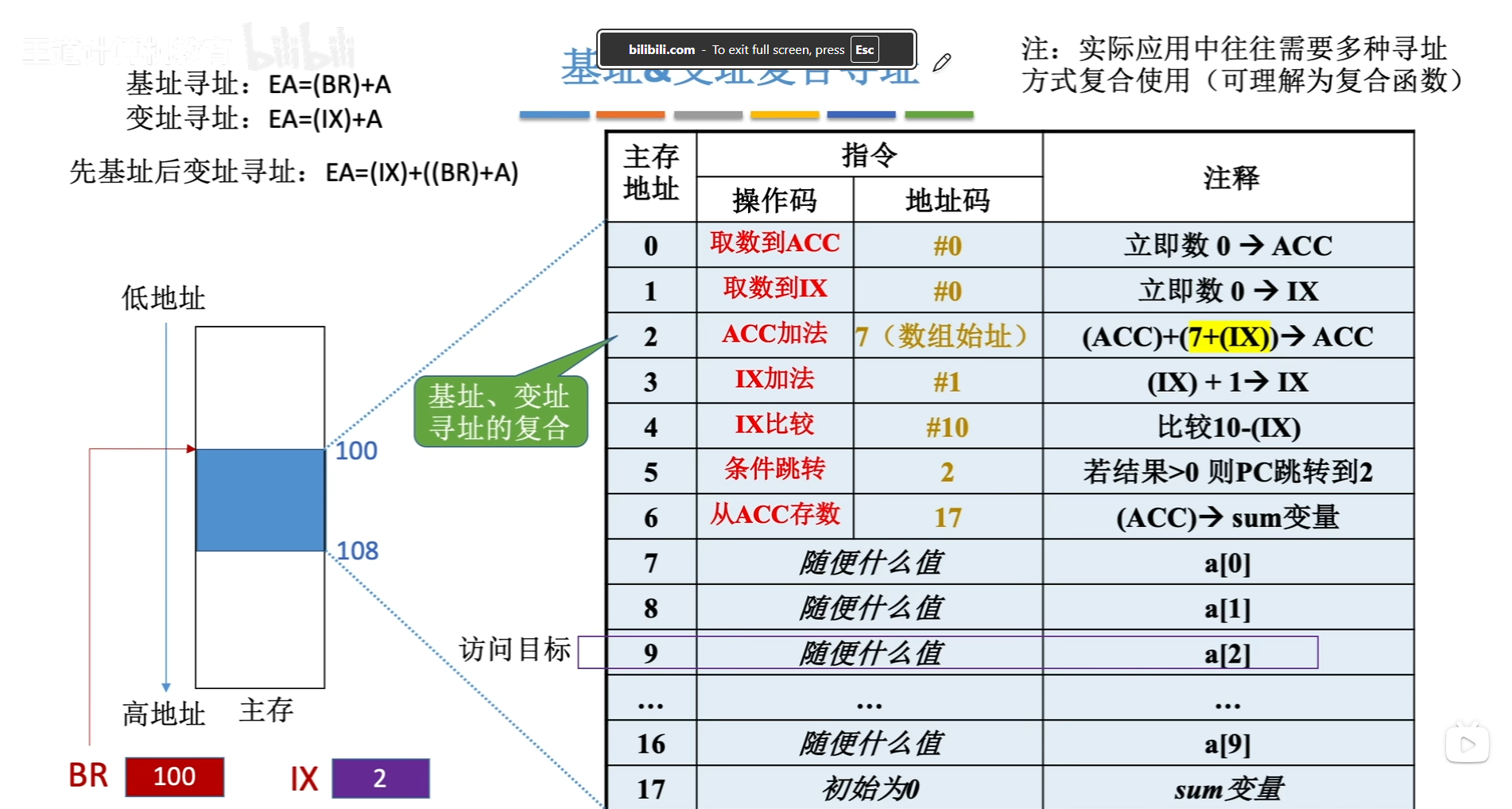
相对寻址
- 把程序计数器PC的内容加上指令格式中的形式地址A而形成操作数的有效地址,即 ,其中A是相对于PC所指地址的位移量,可正可负,补码表示。
- 且注意相对寻址是相对于下一条指令的偏移
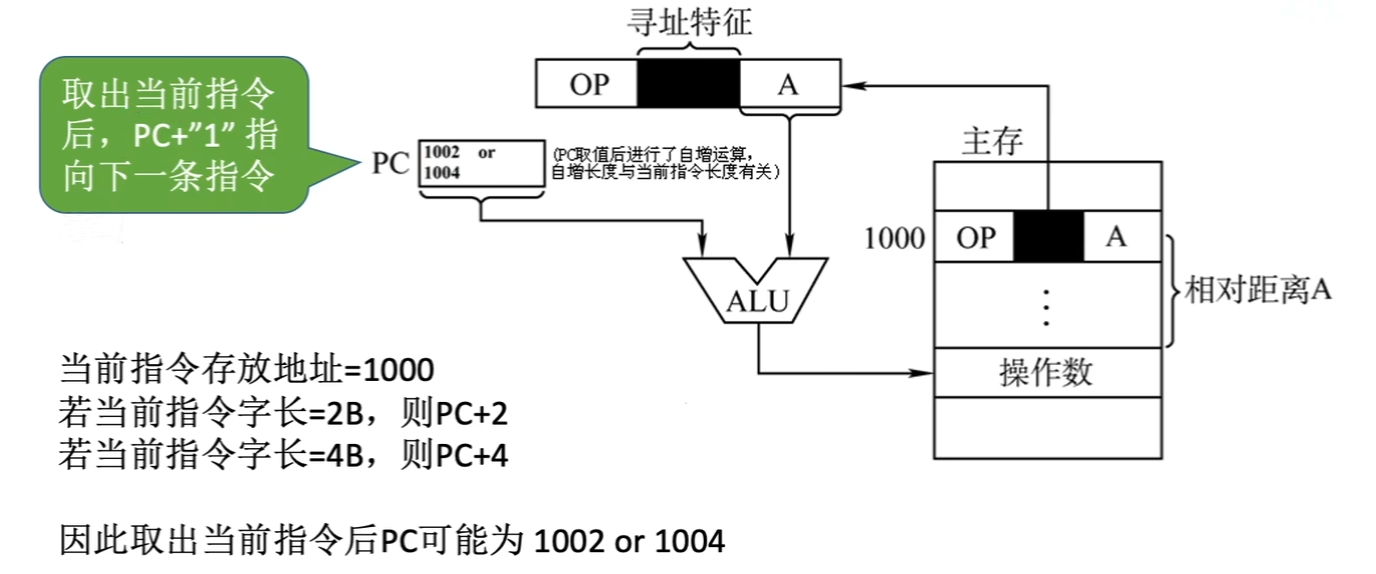
- 如图中的和之前一样的案例,若是我们将这块循环代码的位置进行变换,则之前用了直接寻址的“条件跳转”指令就会失效,而应该改为相对寻址的方式,同时注意要偏移 因为PC自动 的现象
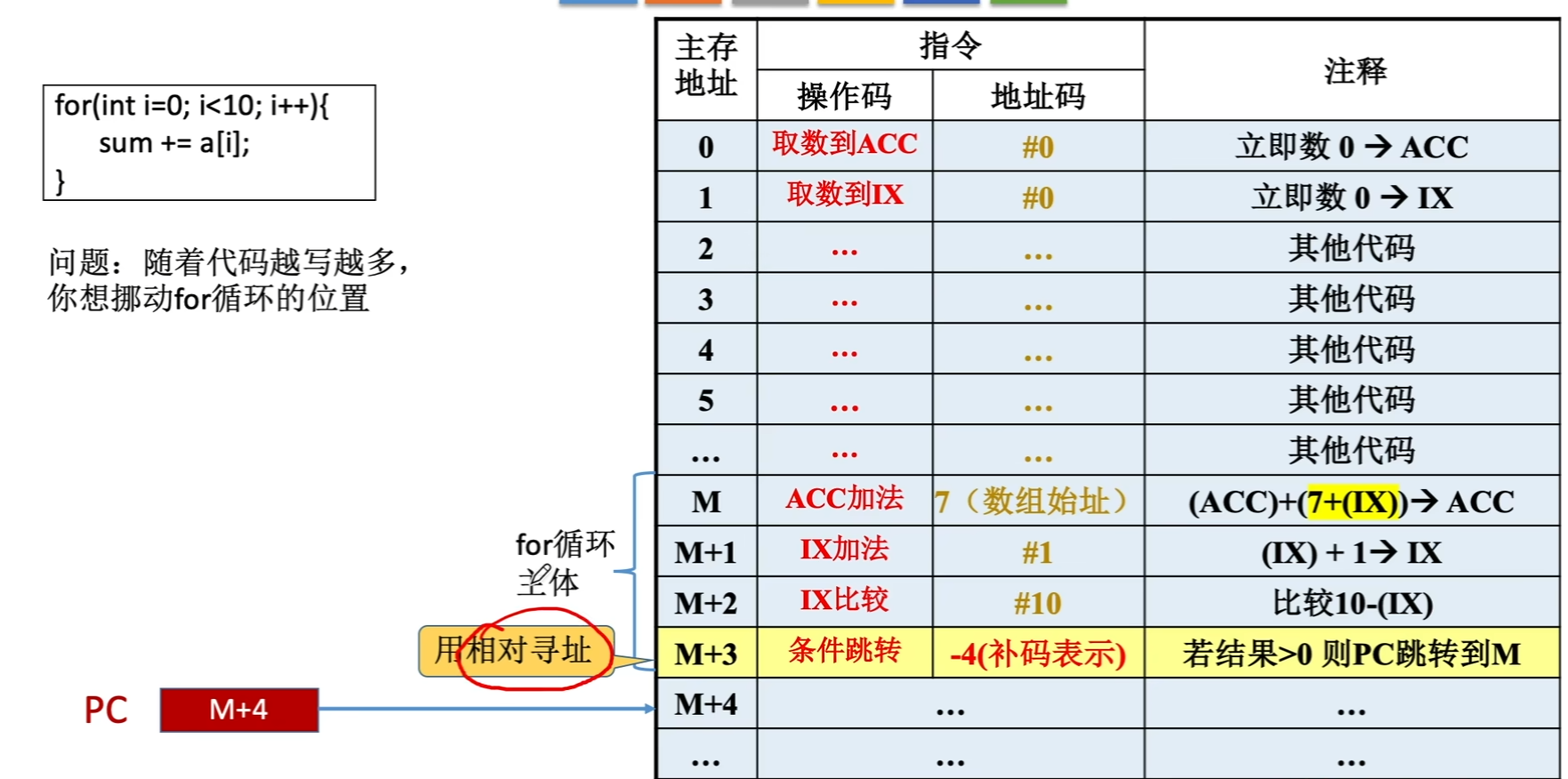
- 优点:操作数的地址不是固定的,它随着PC值的变化而变化,并且与指令地址之间总是相差一个固定值,因此便于程序浮动(一段代码在程序内部的浮动)。相对寻址广泛应用于转移指令。
硬件如何实现数的比较
在上述各例中的"IX比较"和"条件跳转"指令,都对值进行了比较
硬件视角:
- 通过“cmp指令”比较a和b(如cmp a,b),实质上是用a-b相减的结果信息会记录在程序状态字寄存器中(PSW)
- 根据PSW的某几个标志位进行条件判断,来决定是否转移
PSW中有几个比特位记录上次运算的结果
- 位/借位标志CF:最高位有进位/借位时CF=1
- 零标志ZF:运算结果为0则ZF=1,否则ZF=0
- 符号标志SF:运算结果为负,SF=1,否则为0
- 溢出标志OF:运算结果有溢出OF=1否则为0
5.2.3 堆栈寻址
- 操作数存放在堆栈中,隐含使用堆栈指针(SP)作为操作数地址。
- 堆栈是存储器(或专用寄存器组)中一块特定的按“后进先出(LIFO)”原则管理的存储区,该存储区中被读/写单元的地址是用一个特定的寄存器给出的,该寄存器称为堆栈指针(SP)。
- 数据执行出栈或是入栈指令,都要注意SP的变化
硬堆栈
- 使用专门的寄存器来作为堆栈,指令执行期间不需访存,运行速度块,成本高
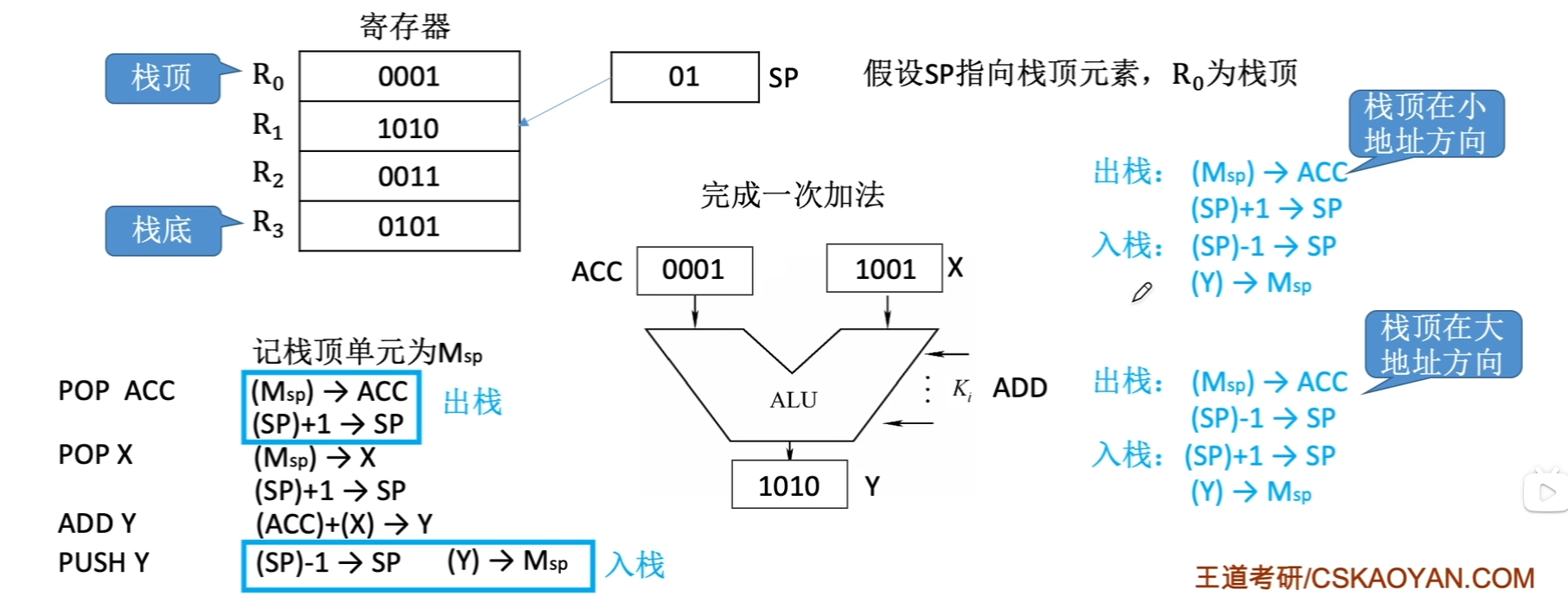
软堆栈
- 用主存中的一块空间作为堆栈。访存次数多,运行速度慢,成本低,也是普遍的堆栈方式
总结
| 寻址方式 | 有效地址 | 访存次数(指令执行期间) |
|---|---|---|
| 隐含寻址 | 程序指定 | 0 |
| 立即寻址 | A即是操作数 | 0 |
| 直接寻址 | 1 | |
| 一次间接寻址 | 2 | |
| 寄存器寻址 | 0 | |
| 寄存器间接一次寻址 | 1 | |
| 相对寻址(转移指令) | 1 | |
| 基址寻址(多道程序) | 1 | |
| 变址寻址(循环程序) | 1 | |
| 堆栈寻址 | 入栈/出栈时EA的确定方式不同 | 硬堆栈不访存,软堆栈访存1次 |
5.3 CISC和RISC
-
CISC: Complex Instruction Set Computer
-
一条指令完成一个复杂的基本功能,一条指令可以由一个专门的电路完成
-
代表: x86架构
-
-
RISC: Reduced Instruction Set Computer
- 一条指令完成一个基本动作,多条指令组合完成一个复杂的基本功能
- 代表: ARM架构
| 对比项目\类别 | CISC | RISC |
|---|---|---|
| 指令系统 | 复杂,庞大 | 简单,精简 |
| 指令数目 | 一般大于200条 | 一般小于100条 |
| 指令字长 | 不固定 | 定长 |
| 可访存指令 | 不加限制 | 只有Load/Store指令 |
| 各种指令执行时间 | 相差较大 | 绝大多数在一个周期内完成 |
| 各种指令使用频度 | 相差很大 | 都比较常用 |
| 通用寄存器数量 | 较少 | 多 |
| 目标代码 | 难以用优化编译生成高效的目标代码程序 | 采用优化的编译程序,生成代码较为高效 |
| 控制方式 | 绝大多数为微程序控制 | 绝大多数为组合逻辑控制 |
| 指令流水线 | 可以通过一定方式实现 | 必须实现 |
6.1 CPU的功能和结构
CPU的功能
- 指令控制:完成取指令、分析指令和执行指令的操作,即程序的顺序控制。
- 操作控制:一条指令的功能往往是由若干操作信号的组合来实现的。CPU管理并产生由内存取出的每条指令的操作信号,把各种操作信号送往相应的部件,从而控制这些部件按指令的要求进行动作。
- 时间控制:对各种操作加以时间上的控制。时间控制要为每条指令按时间顺序提供应有的控制信号。
- 数据加工:对数据进行算术和逻辑运算。
- 中断处理:对计算机运行过程中出现的异常情况和特殊请求进行处理。
运算器和控制器的功能
- 运算器:对数据进行加工。
- 控制器:协调并控制计算机各部件执行程序的指令序列,基本功能包括取指令、分析指令、执行指令。
- 取指令:自动形成指令地址,自动发出取指令的命令。
- 分析指令:操作码译码(分析本条指令要完成什么操作)产生操作数的有效地址。
- 执行指令:根据分析指令得到的“操作命令”和“操作数地址”,形成操作信号控制序列,控制运算器、存储器以及I/O设备完成相应的操作。
- 中断处理:管理总线及输入输出,处理异常情况(如掉电)和特殊请求(如打印机请求打印一行字符)
运算器的基本结构
- 算术逻辑单元(ALU):主要功能是进行算术/逻辑运算。
- 通用寄存器组:如AX、BX、CX、DX、SP等(在x86架构下,AH表示A寄存器高位,AL表示A寄存器低位),用于存放操作数(包括源操作数、目的操作数及中间结果)和各种地址信息等。SP是堆栈指针,用于指示栈顶的地址。
寄存器和ALU有多种连接方式,最直接的就是专用数据通路方式,根据指令执行过程中的数据和地址的流动方向安排连接线路。但是直接用导线连接,相当于多个寄存器同时并且一直向ALU传输数据,但ALU应只能同时处理一对操作数,因此
-
解决方法1:使用多路选择器根据控制信号选择一路输出
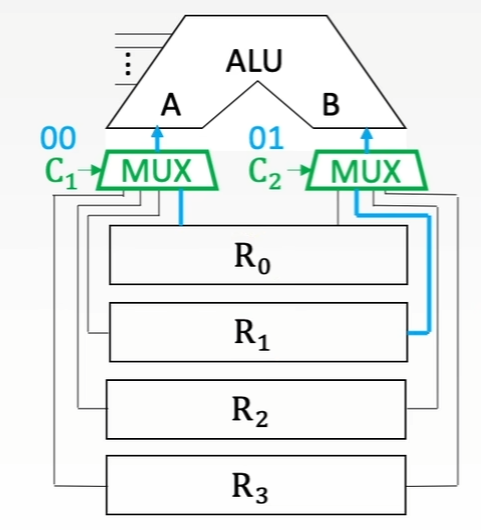
-
解决方法2:使用三态门可以控制每一路是否输出。比如,为1时中的数据输出到A端,
为0时中的数据无法输出到B端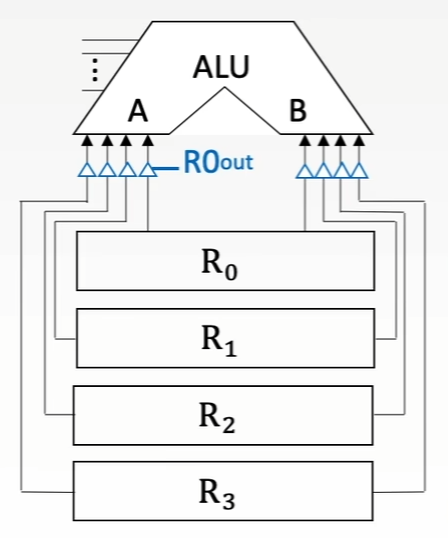
-
专用数据通路方式性能较高,基本不存在数据冲突现象,但结构复杂,硬件量大,不易实现。
另一种连接方式,即CPU内部单总线方式,首先引入一些新的部件
- 暂存寄存器:用于暂存从主存读来的数据,这个数据不能存放在通用寄存器中,否则会破坏其原有内容。
- 累加寄存器(ACC):它是一个通用寄存器,用于暂时存放ALU运算的结果信息,用于实现加法运算。
- 程序状态字寄存器(PSW):保留由算术逻辑运算指令或测试指令的结果而建立的各种状态信息,如溢出标志(OP)、符号标志(SF)、零标志(ZF)、进位标志(CP)等。PSW中的这些位参与并决定微操作的形成。
- 移位器:对运算结果进行移位运算。
- 计数器:控制乘除运算的操作步数。
ALU会通过总线传输运算结果,寄存器也会通过总线向ALU传输操作数,则易发生数据冲突,需要在ALU的输出端加入暂存寄存器和三态门来解决。如,两个操作数分别来自主存和,最后结果存回,那么从主存中取来的操作数直接放入暂存器,就不会破坏运算前的内容。
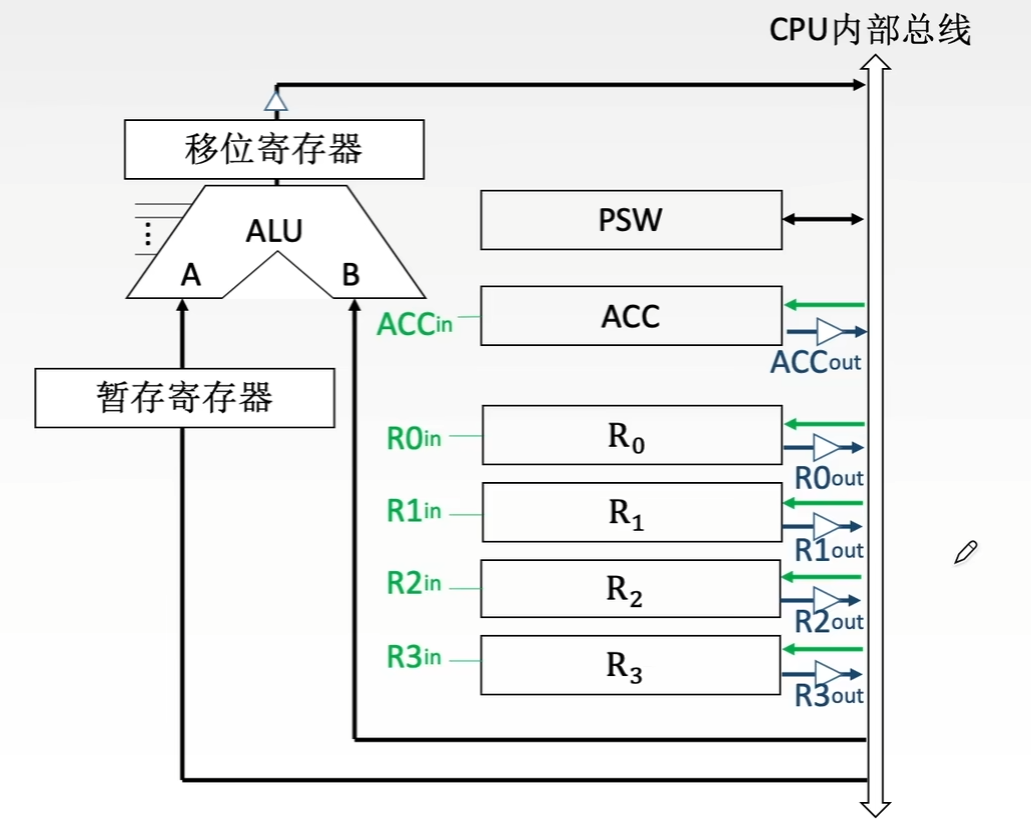
- CPU内部单总线方式,结构简单,容易实现,但数据传输存在较多冲突的现象,性能较低。
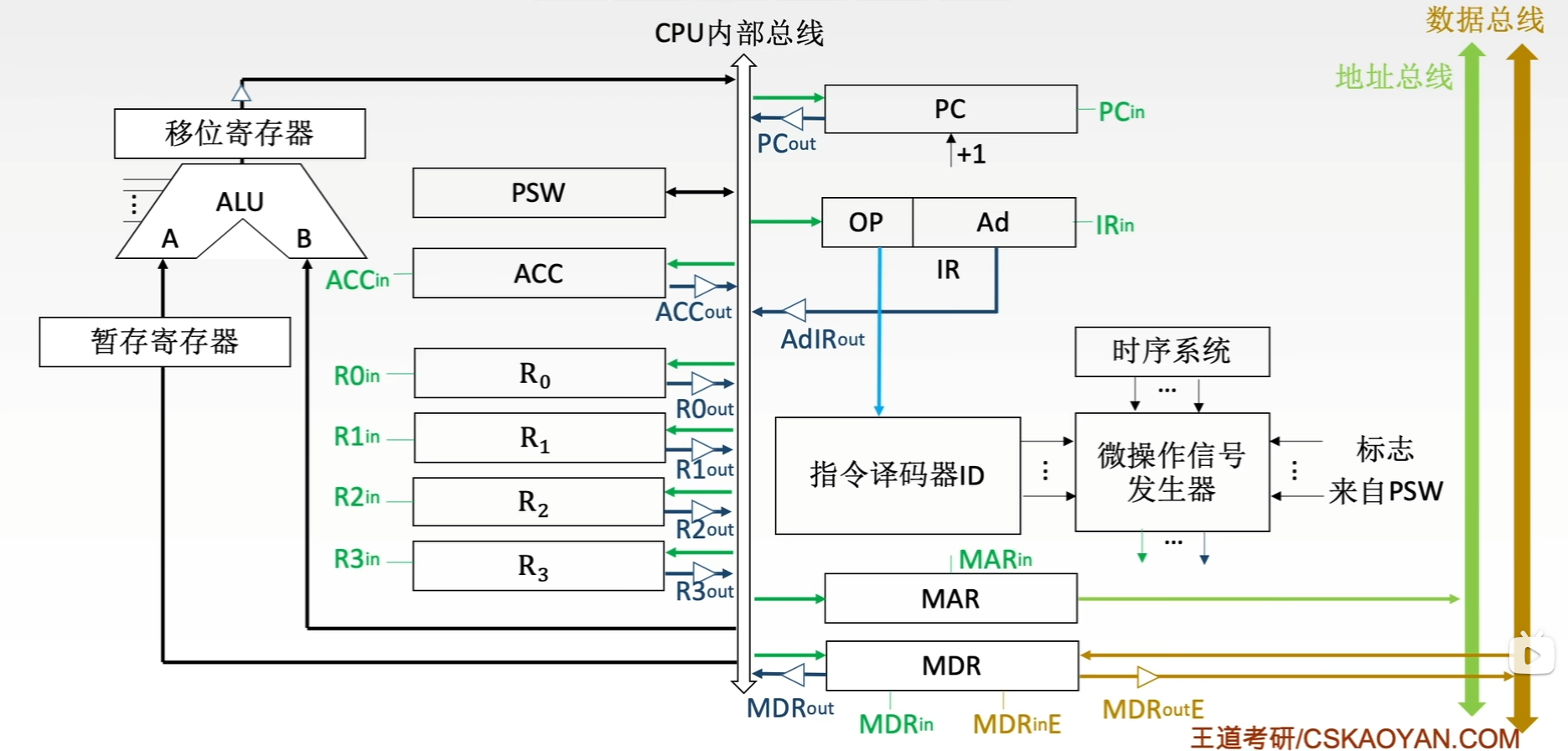
控制器的基本结构
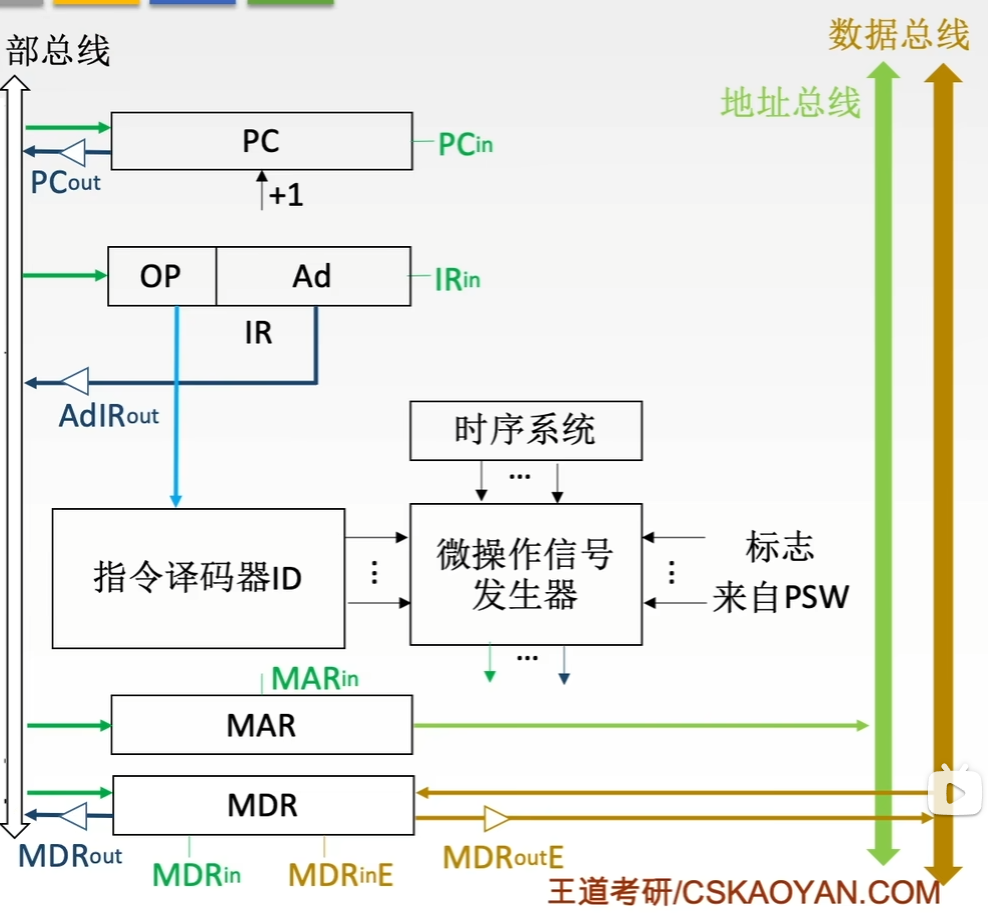
- 程序计数器:用于指出下一条指令在主存中的存放地址。CPU就是根据PC的内容去主存中取指令的。因程序中指令(通常)是顺序执行的,所以PC有自增功能。
- 指令寄存器:用于保存当前正在执行的那条指令。
- 指令译码器:仅对操作码字段进行译码,向控制器提供特定的操作信号。
- 微操作信号发生器:根据IR的内容(指令)、PSW的内容(状态信息)及时序信号,产生控制整个计算机系统所需的各种控制信号,其结构有组合逻辑型和存储逻辑型两种。
- 时序系统:用于产生各种时序信号,它们都是由统一时钟(CLOCK)分频得到。
- 存储器地址寄存器:用于存放所要访问的主存单元的地址。
- 存储器数据寄存器:用于存放向主存写入的信息或从主存中读出的信息。
- 其中,时序系统、微操作信号发生器、指令译码器属于控制单元CU
- 用户可见的寄存器:通用寄存器组、程序状态字寄存器PSW、程序计数器PC
- 用户不可见的寄存器:MAR、MDR、IR、暂存器
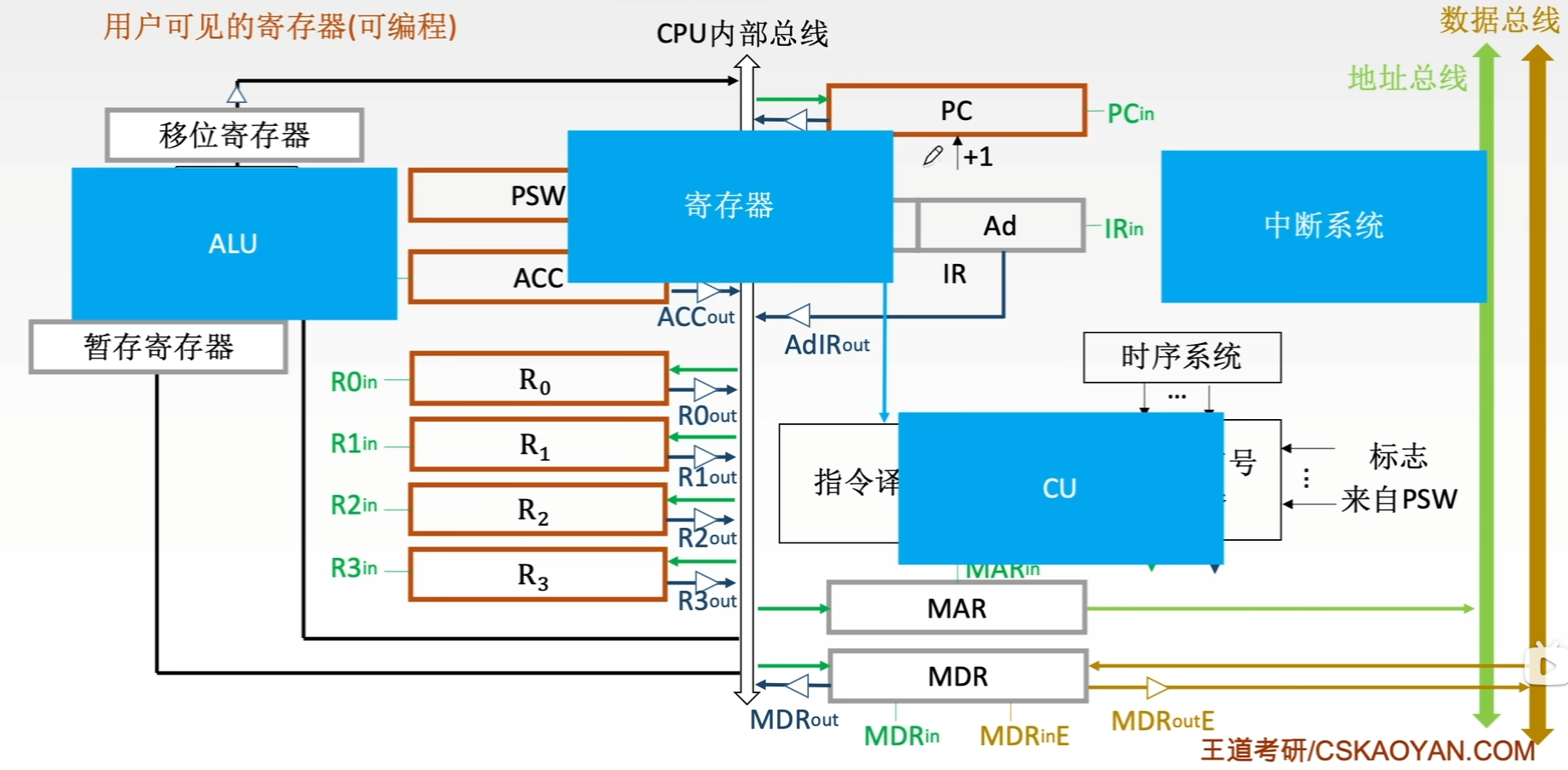
6.2.1 指令周期
-
CPU从主存中每取出并执行一条指令所需的全部时间
-
周期中包括了取指周期和执行周期
- 取指周期包括取指令,对指令译码
- 执行周期包括执行指令
-
指令周期常常用若干机器周期来表示,机器周期又叫CPU周期
- 取指阶段消耗一个CPU周期
- 执行阶段又消耗一个CPU周期
-
一个机器周期又包含若干时钟周期(也称为节拍、T周期或CPU时钟周期)它是CPU操作的最基本单位。
- 如图中所示,取指令的机器周期( ~ ) 包括了4个微操作
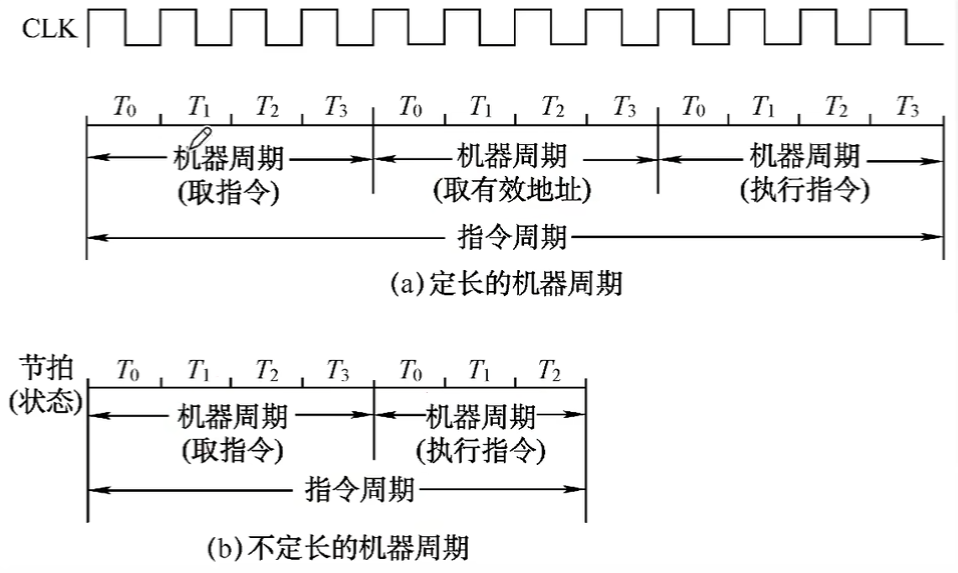
- 一个机器周期中的时钟周期数量不一定相等,一个指令周期中的机器周期的数量也不一定相同,所以分为了定长的机器周期和不定长的机器周期
- 如空指令(NOP)的指令周期只有一个机器周期,即取指周期,从主存中取出指令
- 如乘法指令的指令周期包含了取指周期,和较长的执行周期,进行指令的执行
- 若是具有间接寻址的指令,在取指周期和执行周期间,包含了间址周期,用来将形式地址转化为实际地址,得到操作数的有效地址。有些会在指令周期的最后加入中断周期
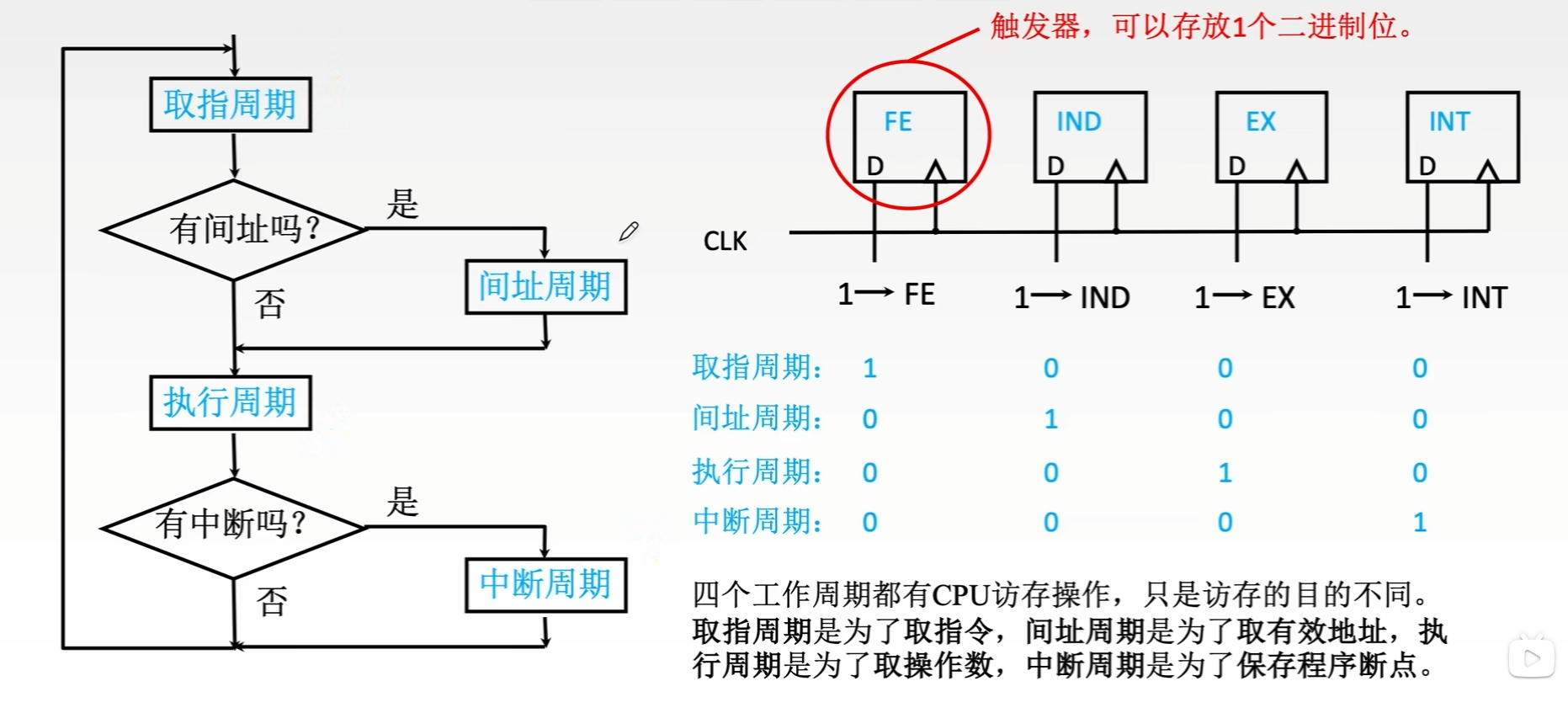
6.2.2 指令周期的数据流
取指周期
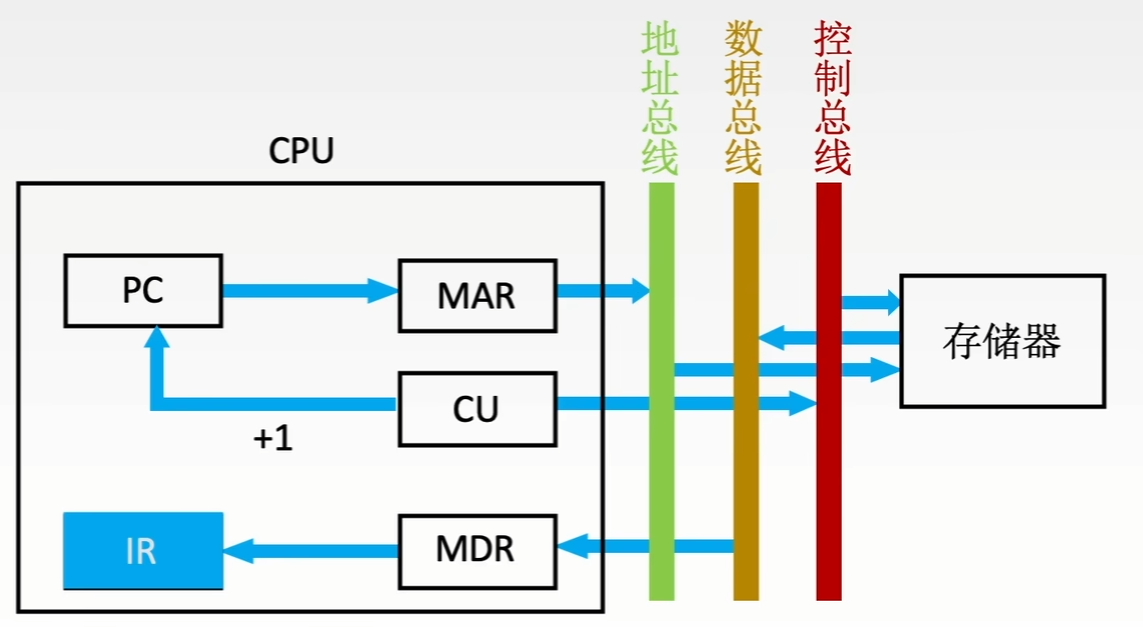
- 当前指令地址送至存储器地址寄存器,记做:(PC) → MAR
- CU发出控制信号,经控制总线传到主存,这里是读信号,记做:1 → R
- 将MAR所指主存中的内容经数据总线送入MDR,记做:M(MAR) → MDR
- 将MDR中的内容(此时是指令)送入IR,记做:MDR → IR
- CU发出信号,形成下一条指令地址,记做:(PC)+1 → PC
间址周期
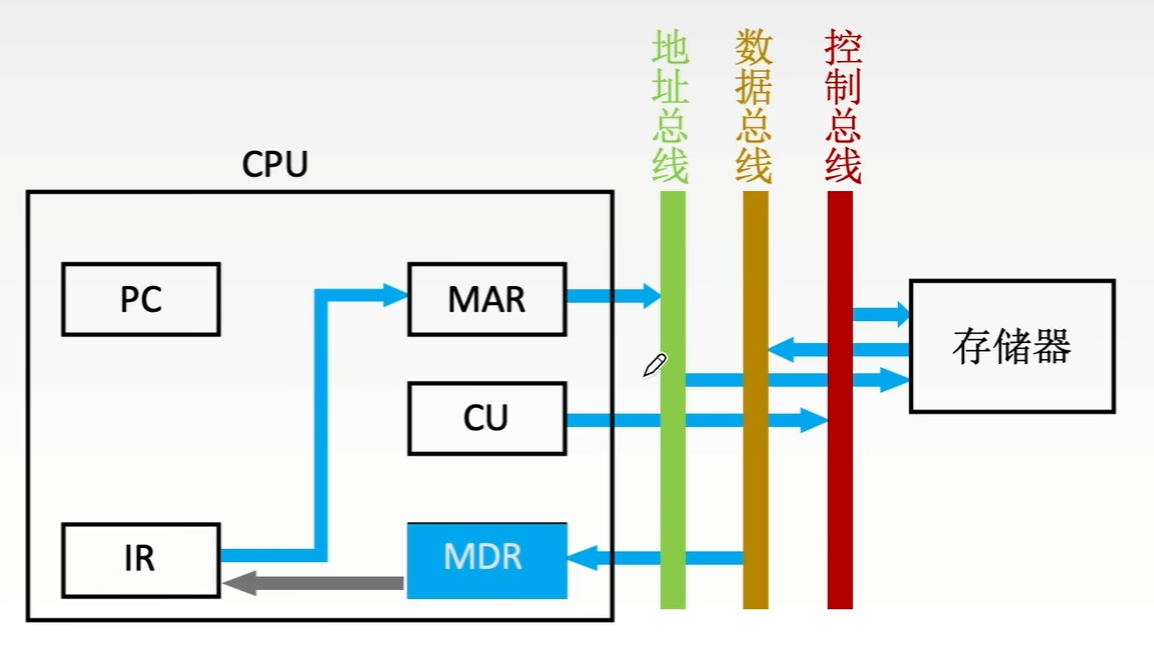
- 将指令的地址码送入MAR,记做:Ad(IR) → MAR 或Ad(MDR) → MAR
- CU发出信号,启动主存做读操作,记做:1 → R
- 将MAR所指主存中的内容经数据总线送入MDR,记做:M(MAR) → MDR
- 有效地址送至指令的地址码字段,记做:MDR → Ad(IR)
中断周期
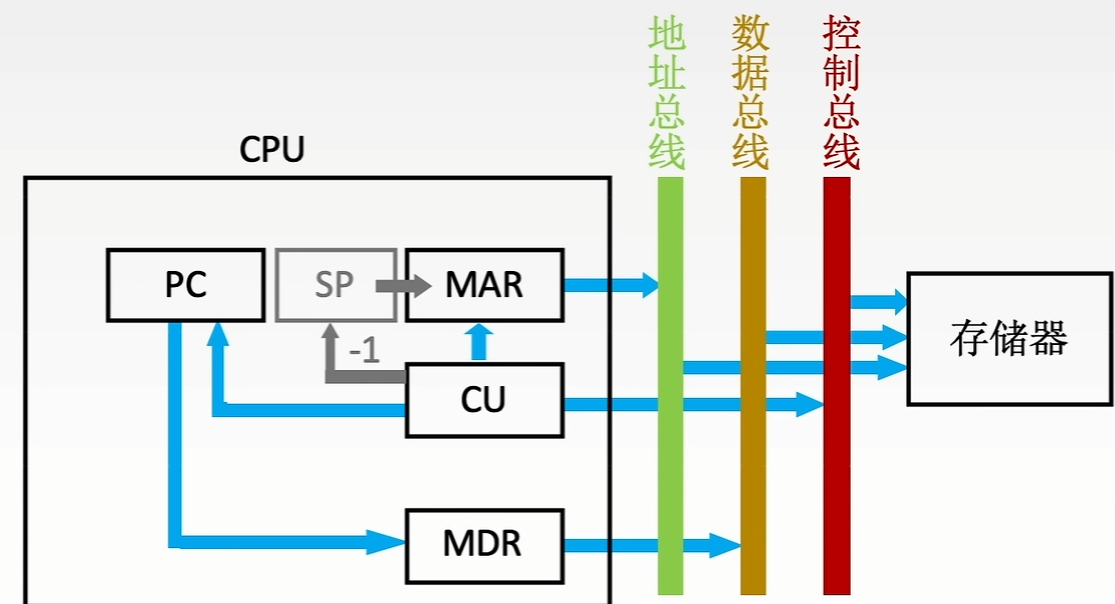
- 中断,暂停当前任务去完成其他任务。为了能够恢复当前任务,需要保存断点。一般使用堆栈来保存断点,这里用SP表示栈顶地址,假设SP指向栈顶元素,进栈操作是先修改指针,后存入数据。
- CU控制将SP减1,修改后的地址送入MAR 记做:(SP)-1 → SP,(SP) → MAR 本质上是将断点存入某个存储单元,假设其地址为a,故可记做:a → MAR
- CU发出信号,启动主存做写操作, 记做:1 → W
- 将断点(PC内容)送入MDR, 记做:(PC) → MDR
- CU控制将中断服务程序的入口地址(由向量地址形成部件产生)送入PC, 记做:向量地址 → PC
6.2.3 指令执行方案
单指令周期
- 对所有指令都选用相同的执行时间来完成。
- 指令之间串行执行;指令周期取决于执行时间最长的指令的执行时间。
- 对于那些本来可以在更短时间内完成的指令,要使用这个较长的周期来完成,会降低整个系统的运行速度。
多指令周期
- 对不同类型的指令选用不同的执行步骤来完成。
- 指令之间串行执行;可选用不同个数的时钟周期来完成不同指令的执行过程。
- 需要更复杂的硬件设计。
流水线
- 在每一个时钟周期启动一条指令,尽量让多条指令同时运行,但各自处在不同的执行步骤中。
- 指令之间并行执行。
6.3.1 数据通路 单总线结构
寄存器之间数据传送
比如把PC内容送至MAR,实现传送操作的流程及控制信号为:
- (PC) → Bus
- 有效,PC内容送总线
- Bus → MAR
- 有效,总线内容送MAR
主存与CPU之间的数据传送
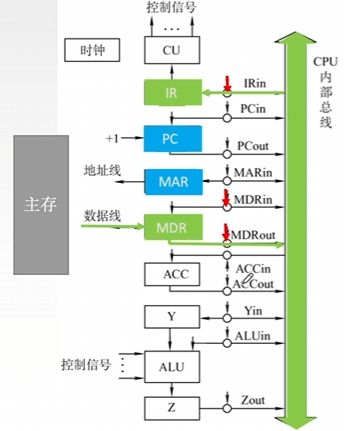
比如CPU从主存读取指令,实现传送操作的流程及控制信号为:
-
(PC) → Bus → MAR
和有效,现行指令地址 → MAR
-
1 → R
CU发读命令(通过控制总线发出,图中未画出)
-
MEM(MAR) → MDR
有效
-
MDR → Bus → IR
和有效,现行指令→IR
执行算术或逻辑运算
比如一条加法指令,微操作序列及控制信号为:
-
Ad(IR) → Bus → MAR
和有效
-
1 → R
CU发读命令
-
MEM(MAR) → 数据线 → MDR
有效
-
MDR → Bus → Y
和有效,操作数→Y
-
(ACC) + Y → Z
和有效,CU向ALU发送加命令
-
Z → ACC
和有效,结果→ACC
例题
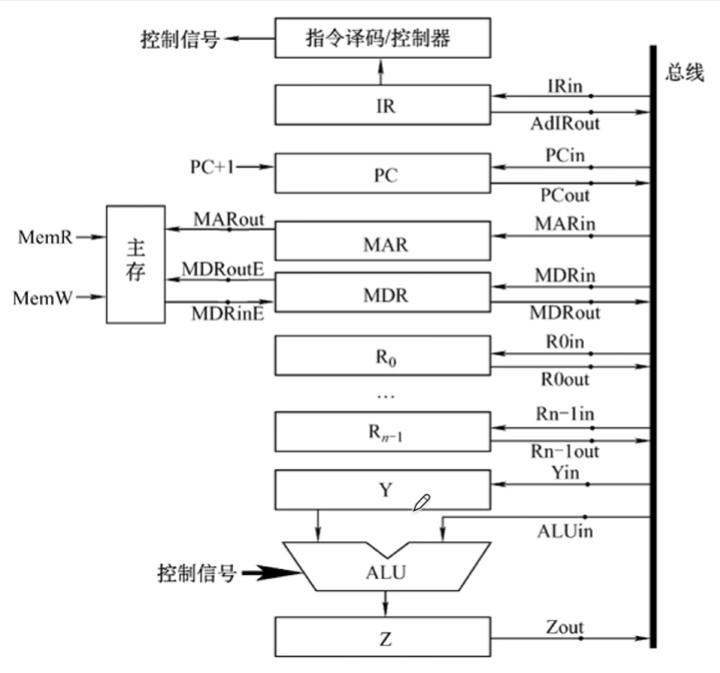
设有如图所示的单总线结构,分析指令ADD (R0),R1 的指令流程和控制信号
(R0)是目的操作数,R1是源操作数,R0有括号说明R0中存放的是操作数在主存的地址而非操作数本身,所以要对其进行间接寻址操作
-
分析指令功能和指令周期
-
功能:((R0)) + (R1) → (R0)
把计算结果放回R0所指向的存储单元
-
取指周期、间址周期、执行周期
-
-
取值周期
时序 微操作 有效控制信号 1 (PC) → MAR PCout,MARin 2 M(MAR) → MDR (PC)+1 → PC MemR,MARout,MDRinE 3 (MDR) → IR MDRout,IRin 4 指令译码 - -
间址周期
完成取数操作,被加数在主存中,加数已经放在寄存器R1中
时序 微操作 有效控制信号 1 (R0) → MAR R0out,MARin 2 M(MAR) → MDR MemR,MARout,MDRinE 3 (MDR) → Yin MDRout,Yin -
执行周期
完成取数操作,被加数在主存中,加数已经放在寄存器R1中
时序 微操作 有效控制信号 1 (R1)+(Y)→Z R1out,ALUin,CU向ALU发ADD控制信号 2 (Z)→MDR Zout,MDRin 3 (MDR)→M(MAR) MemW,MDRoute,MARout
6.3.2 数据通路 专用数据通路
skip
6.4.1 硬布线控制器
- 微操作控制信号由组合逻辑电路根据当前的指令码、状态和时序,即时产生。
6.4.2 微程序控制器的基本原理
设计思路
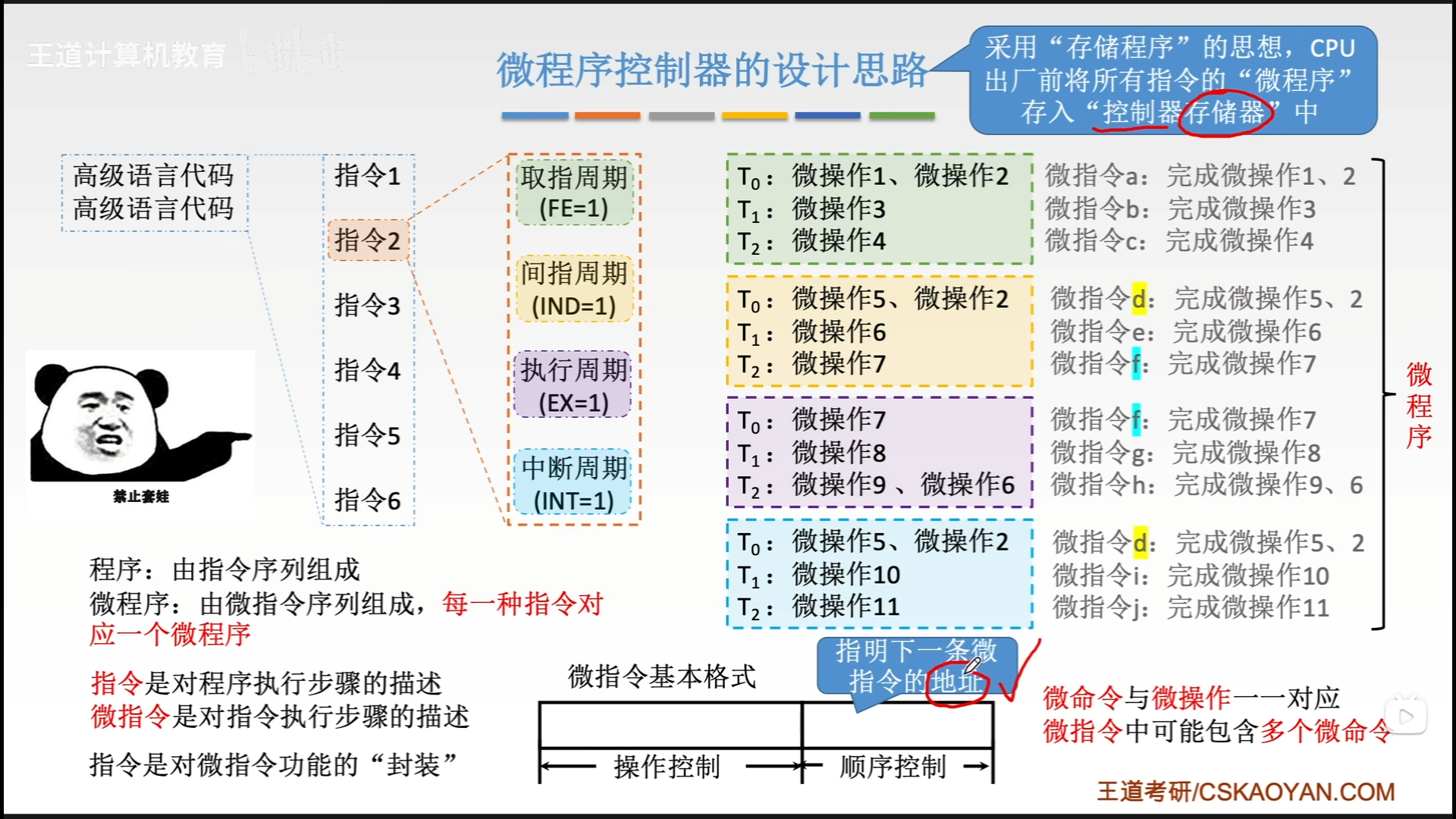
基本结构
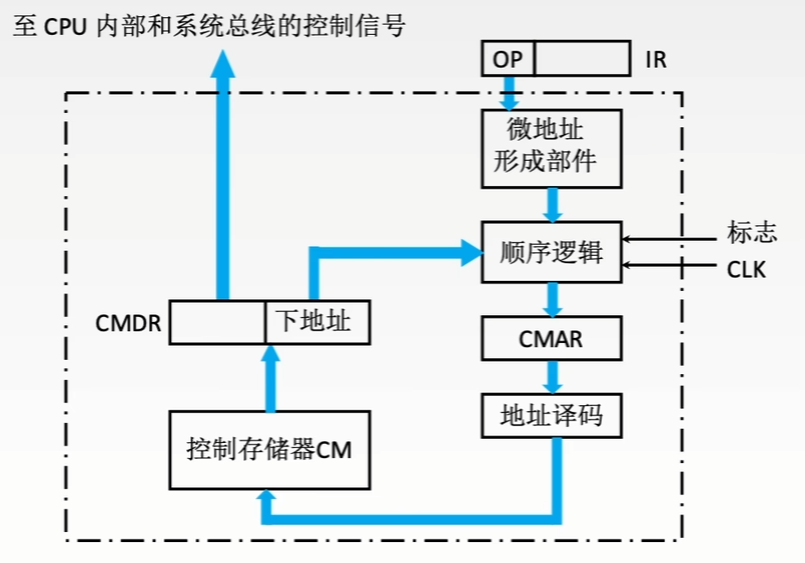
- 微地址形成部件:微地址即微指令在CM中的存放地址,通过指令操作码形成对应微程序的第一条微指令的存放地址。
- 顺序逻辑:根据某些机器标志和时序信息确定下一条微指令的存放地址。
- CMAR(μPC):微地址寄存器,指明接下来要执行的微指令的存放地址,大致相当于CPU中MAR和PC的组合体。
- 地址译码器:将CMAR内的地址信息译码为电信号,控制CM读出微指令。
- 控制存储器CM:存放所有指令对应的微程序(微指令序列)用ROM实现,按地址寻址。通常在CPU出厂时就把所有微程序写入。
- CMDR(μIR):微指令寄存器,用于存放当前要执行的微指令。CM(μPC)→μIR。大致相当于CPU中MDR和IR的组合体。
工作原理
-
取指周期、间址周期、中断周期的微程序是可以共享的,控存中只需存储一份
- 故如果某指令系统中有n条机器指令,则CM中微程序的个数至少是n+1个。
- 间址、中断周期可有可无。
-
假设接下来执行LDA指令(把主存中的数据放入ACC)
- 在取指周期的最后,程序不一定需要进入首地址为3的间址周期,而有可能直接进入执行周期,这需要顺序逻辑来指明接下来要执行的地址。中断周期也是同理。
-
微周期(微指令周期):从控存取出一条微指令并执行相应的微操作所需的时间。
6.4.3 微指令的设计
格式
- 相容性微命令:可以并行完成的微命令。
- 互斥性微命令:不允许并行完成的微命令。
水平型微指令
- 一条微指令能定义多个可并行的微命令。
- 基本格式由操作控制和顺序控制组成。
- 优点:微程序短的情况,执行速度块。缺点:微指令长的情况,编写微程序较麻烦。
垂直型微指令
- 一条微指令只能定义一个微命令,由微操作码字段规定具体功能。
- 基本格式由微操作码、目的地址和源地址组成。
- 优点:微指令短、简单、规整,便于编写微程序。缺点:微程序长,执行速度慢,工作效率低。
混合型微指令
- 在垂直型的基础上增加一些不太复杂的并行操作。
- 微指令较短,仍便于编写;微程序也不长,执行速度加快。
编码方式(控制方式)
- 微指令的编码方式又称为微指令的控制方式,它是指如何对微指令的控制字段进行编码,以形成控制信号。编码的目标是在保证速度的情况下,尽量缩短微指令字长。
下面讨论的均为水平型微指令的编码(控制)方式
直接编码方式
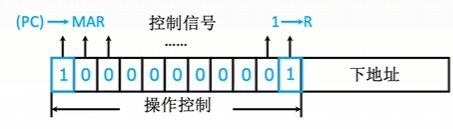
- 在微指令的操作控制字段中,每一位代表一个微操作命令
- 某位为“1”表示该控制信号有效
- 优点:简单、直观,执行速度快,操作并行性好。缺点:微指令字长过长,n个微命令就要求微指令的操作字段有n位,造成控存容量极大。
字段直接编码方式
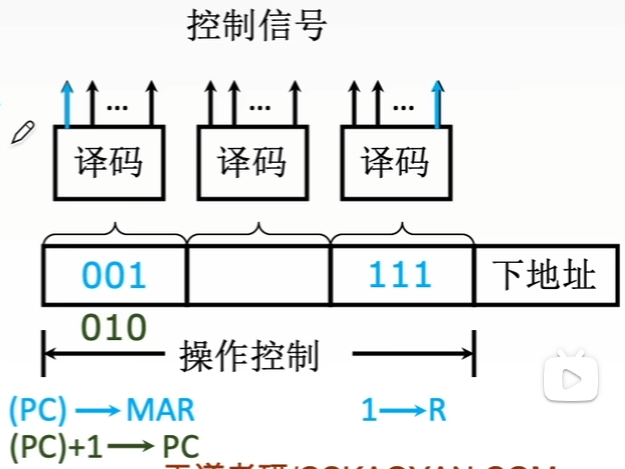
-
将微指令的控制字段分成若干“段”,每段经译码后发出控制信号。微命令字段分段的原则:
- 互斥性微命令分在同一段内,相容性微命令分在不同段内。
- 每个小段中包含的信息位不能太多,否则将增加译码线路的复杂性和译码时间。
- 一般每个小段还要留出一个状态,表示本字段不发出任何微命令。因此,当某字段的长度为3位时,最多只能表示7个互斥的微命令。通常用000表示不操作。
-
优点:可以缩短微指令字长。缺点:要通过译码电路后再发出微命令,因此比直接编码方式慢。
-
例题:某计算机的控制器采用微程序控制方式,微指令中的操作控制字段采用字段直接编码法,共有33个微命令,构成5个互斥类,分别包含7、3、12、5和6个微命令,则操作控制字段至少有多少位?
第1个互斥类有7个微命令,要留出1个状态表示不操作,所以需要表示8种不同的状态,故需要3个二进制位。
以此类推,后面4个互斥类各需要表示4、13、6、7种不同的状态,分别对应2、4、3、3个二进制位。
故操作控制字段的总位数为 3+2+4+3+3 = 15 位。
Tips:若采用直接编码方式,则控制字段需要33位。
字段间接编码方式
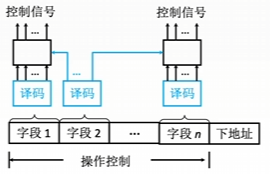
- 一个字段的某些微命令需由另一个字段中的某些微命令来解释,由于不是靠字段直接译码发出的微命令,故称为字段间接编码,又称隐式编码。
- 优点:可进一步缩短微指令字长。缺点:削弱了微指令的并行控制能力,故通常作为字段直接编码方式的一种辅助手段。
地址形成方式
-
微指令的下地址字段指出
微指令格式中设置一个下地址字段,由微指令的下地址字段直接指出后继微指令的地址,这种方式又称为断定方式。
-
根据机器指令的操作码形成
当机器指令取至指令寄存器后,微指令的地址由操作码经微地址形成部件形成。
-
增量计数器法
(CMAR)+1 → CMAR
-
分支转移
指明判别条件和转移成功后的去向
-
通过测试网络
-
由硬件产生微程序入口地址
第一条微指令地址 由专门硬件产生(用专门的硬件记录取指周期微程序首地址)
中断周期 由硬件产生 中断周期微程序首地址(用专门的硬件记录)
-
例题:某计算机采用微程序控制器,共有32条指令,公共的取指令微程序包含2条微指令,各指令对应的微程序平均由4条微指令组成,采用断定法(下地址字段法)确定下条微指令地址,则微指令中下地址字段的位数至少是多少位?
“至少”说明不需要间址和中断周期,只需额外计算取指周期的2条
总共需要存储多少条微指令? 32×4+2 = 130条
标注出130个不同的位置至少需要多少个二进制位? ,
下地址字段的位数至少是8位
6.4.4 微程序控制单元的设计
设计步骤
-
分析每个阶段的微操作序列
-

-
以取值周期为例,相比于硬布线的方式,若要读出微指令以及转入下一个机器周期,都需要多一个节拍
- 取指周期的第一条微指令地址由硬件自动给出,下一条指令的地址在当前执行的指令的下地址字段
- Ad(CMDR)→CMAR 用当前微指令的下地址表示找到下一条微指令
- 微地址形成部件→CMAR
-
-
写出对应机器指令的微操作命令及节拍安排
-
写出每个周期所需要的微操作
-
补充微程序控制器特有的微操作
- 取指周期:Ad(CMDR)→CMAR 每条微指令结束之后都要进行,OP(IR)→微地址形成部件→CMAR 取值周期的最后一条微指令完成后,要根据指令操作码确定其执行周期的微程序首地址
- 执行周期:Ad(CMDR)→CMAR 每条微指令结束之后都要进行
-
-
确定微指令格式
- 根据微操作个数决定采用何种编码方式,以确定微指令的操作控制字段的位数。根据CM中存储的微指令总数,确定微指令的顺序控制字段的位数。最后按操作控制字段位数和顺序控制字段位数就可确定微指令字长。
-
编写微指令码点
- 根据操作控制字段每一位代表的微操作命令,编写每一条微指令的码点。
微程序设计分类
- 静态微程序分类和动态微程序设计
- 静态:微程序无需改变,采用ROM
- 动态:通过改变微指令和微程序改变机器指令,有利于仿真,采用EPROM
- 毫微程序设计
硬布线与微程序的比较
| 类别 | 微程序控制器 | 硬布线控制器 |
|---|---|---|
| 工作原理 | 微操作控制信号以微程序的形式存放在控制存储器中,执行指令时读出即可 | 微操作控制信号由组合逻辑电路根据当前的指令码、状态和时序,即时产生 |
| 执行速度 | 慢 | 快 |
| 规整性 | 较规整 | 烦琐、不规整 |
| 应用场合 | CISC CPU | RISC CPU |
| 易扩充性 | 易扩充修改 | 困难 |
6.5.1 指令流水线 基本概念和性能指标
基本概念
- 一条指令的执行过程可以分成多个阶段(或过程)。根据计算机的不同,具体的分法也不同。
- 取指:根据PC内容访问主存储器,取出一条指令送到IR中。
- 分析:对指令操作码进行译码,按照给定的寻址方式和地址字段中的内容形成操作数的有效地址EA,并从有效地址EA中取出操作数。
- 执行:根据操作码字段,完成指令规定的功能,即把运算结果写到通用寄存器或主存中。
设取指、分析、执行3个阶段的时间都相等,用t表示,按以下几种执行方式分析n条指令的执行时间
-
顺序执行方式
-

- 总耗时
- 传统冯·诺依曼机采用顺序执行方式,又称串行执行方式。优点:控制简单,硬件代价小。缺点:执行指令的速度较慢,在任何时刻,处理机中只有一条指令在执行,各功能部件的利用率很低。
-
-
一次重叠执行方式
-

- 总耗时
- 优点:程序的执行时间缩短了1/3,各功能部件的利用率明显提高。缺点:需要付出硬件上较大开销的代价,控制过程也比顺序执行复杂了。
-
-
二次重叠执行方式
-

- 总耗时
- 与顺序执行方式相比,指令的执行时间缩短近2/3。这是一种理想的指令执行方式,在正常情况下,处理机中同时有3条指令在执行。
-
除了上面的用指令执行过程图来表示流水线,主要用来分析指令执行过程以及影响流水线的因素。
还有用时空图来表示流水线,主要用于分析流水线的性能。
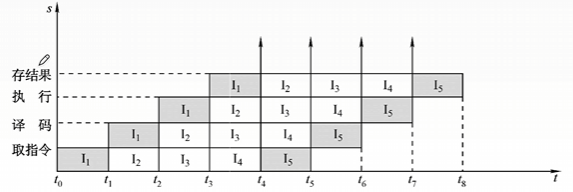
性能指标
吞吐率
-
吞吐率是指在单位时间内流水线所完成的任务数量,或是输出结果的数量。设任务数为n;处理完成n个任务所用的时间为
-
则计算流水线吞吐率(TP)的最基本公式为 , ,流水线的实际吞吐率为 ,当连续输入的任务 时,得最大吞吐率为 。
理想情况下,流水线的时空图如下:
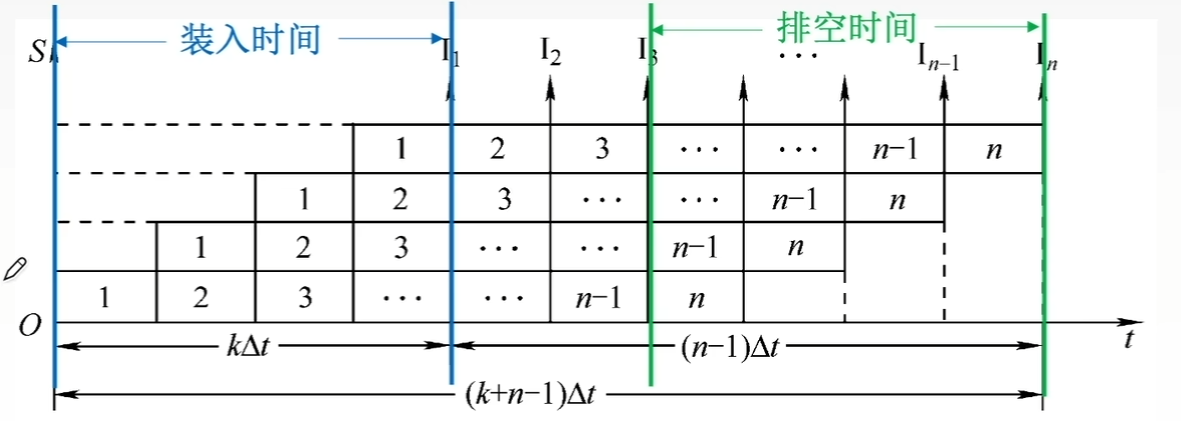
-
一条指令的执行分为k个阶段,每个阶段耗时 ,一般取 一个时钟周期
加速比
-
加速比是完成同样一批任务,不使用流水线所用的时间与使用流水线所用的时间之比。
-
设 表示不使用流水线时的执行时间,即顺序执行所用的时间; 表示使用流水线时的执行时间。则计算流水线加速比(S)的基本公式为 当连续输入的任务 时,最大加速比为
-
单独完成一个任务耗时为 ,则顺序完成n个任务耗时 ,
-
实际加速比为
效率
-
流水线的设备利用率称为流水线的效率
-
在时空图上,流水线的效率定义为完成n个任务占用的时空区有效面积与n个任务所用的时间与k个流水段所围成的时空区总面积之比。
理想情况下,流水线的时空图如下:
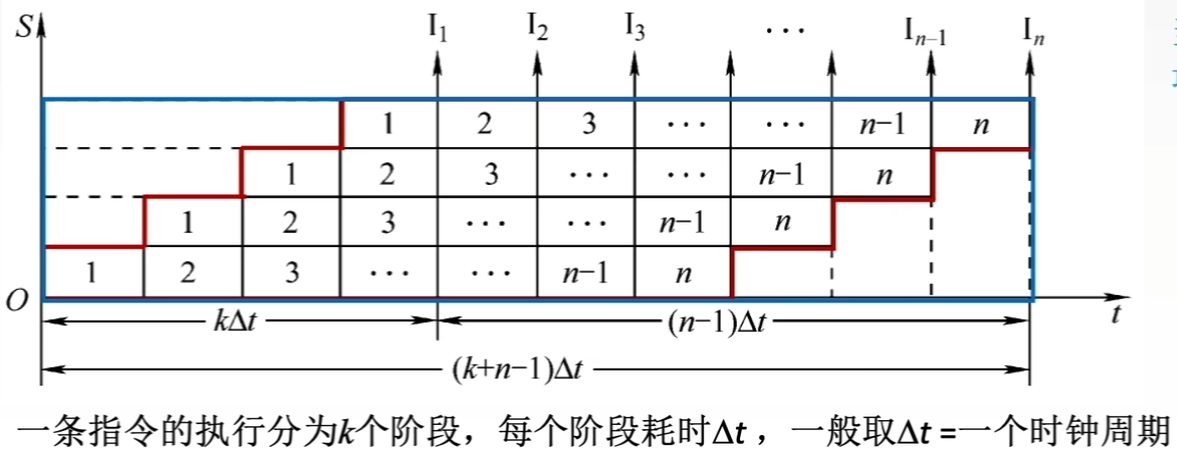
-
则流水线效率(E)的一般公式为
-
当连续输入的任务 时,最高效率为
6.5.2 指令流水线影响因素分类
为方便流水线的设计,将每个阶段的耗时取成一样,以最长耗时为准。
流水线每一个功能段部件后面都要有一个缓冲寄存器,或称为锁存器,其作用是保存本流水段的执行结果,提供给下一流水段使用。
结构相关(资源冲突)
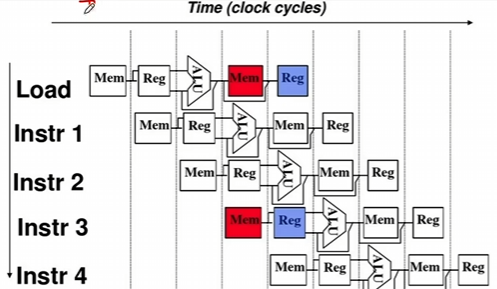
- 由于多条指令在同一时刻争用同一资源而形成的冲突称为结构相关。
- 如图所示,Load和Instr3在同一时刻访问了主存和寄存器,造成冲突。
- 解决方法:
- 1.后一指令暂停一周期。
- 2.数据存储器+指令存储器,分开存储。
数据相关(数据冲突)
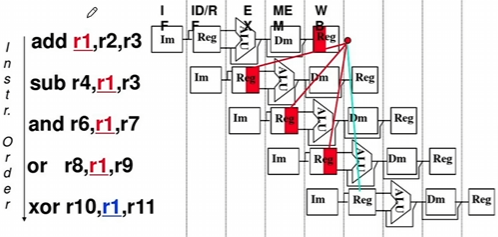
- 数据相关指在一个程序中,存在必须等前一条指令执行完才能执行后一条指令的情况,则这两条指令即为数据相关。
- 如图所示,第一条指令执行 但是在r1被写回寄存器之前,后面的指令在前面的时刻就进行了调用,造成冲突。
- 解决方法:
- 1.把遇到数据相关的指令及其后续指令都暂停一至几个时钟周期,直到数据相关问题消失后再继续执行。可分为硬件阻塞(stall)和软件插入"NOP(空指令)"两种方法。
- 2.数据旁路技术(转发机制)如在上图,将第一条指令的ALU连接至下一条指令的ALU,在不用写回寄存器的情况下即可使用此操作数。
- 3.编译优化,通过编译器调整指令顺序来解决,如将后面无冲突的指令更早运行。
控制相关(控制冲突)
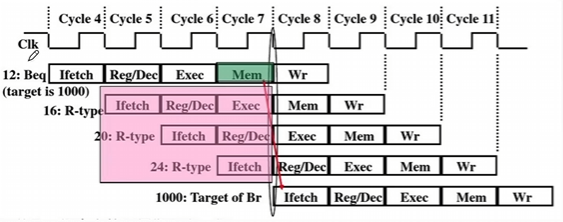
- 当流水线遇到转移指令和其它改变PC值的指令而造成断流时,会引起控制相关。
- 如图所示,第一条指令为条件转移,若是不满足条件,指令顺序执行,若是满足条件,可能发生跳转,中间的指令不执行。
- 解决方法:
- 1.转移指令分支预测:简单预测(永远猜true或false)动态预测(根据历史情况动态调整)。
- 2.预取转移成功和不成功两个控制流方向上的目标指令。
- 3.加快和提前形成条件码。
- 4.提高转移方向的猜准率。
7.1 总线概述
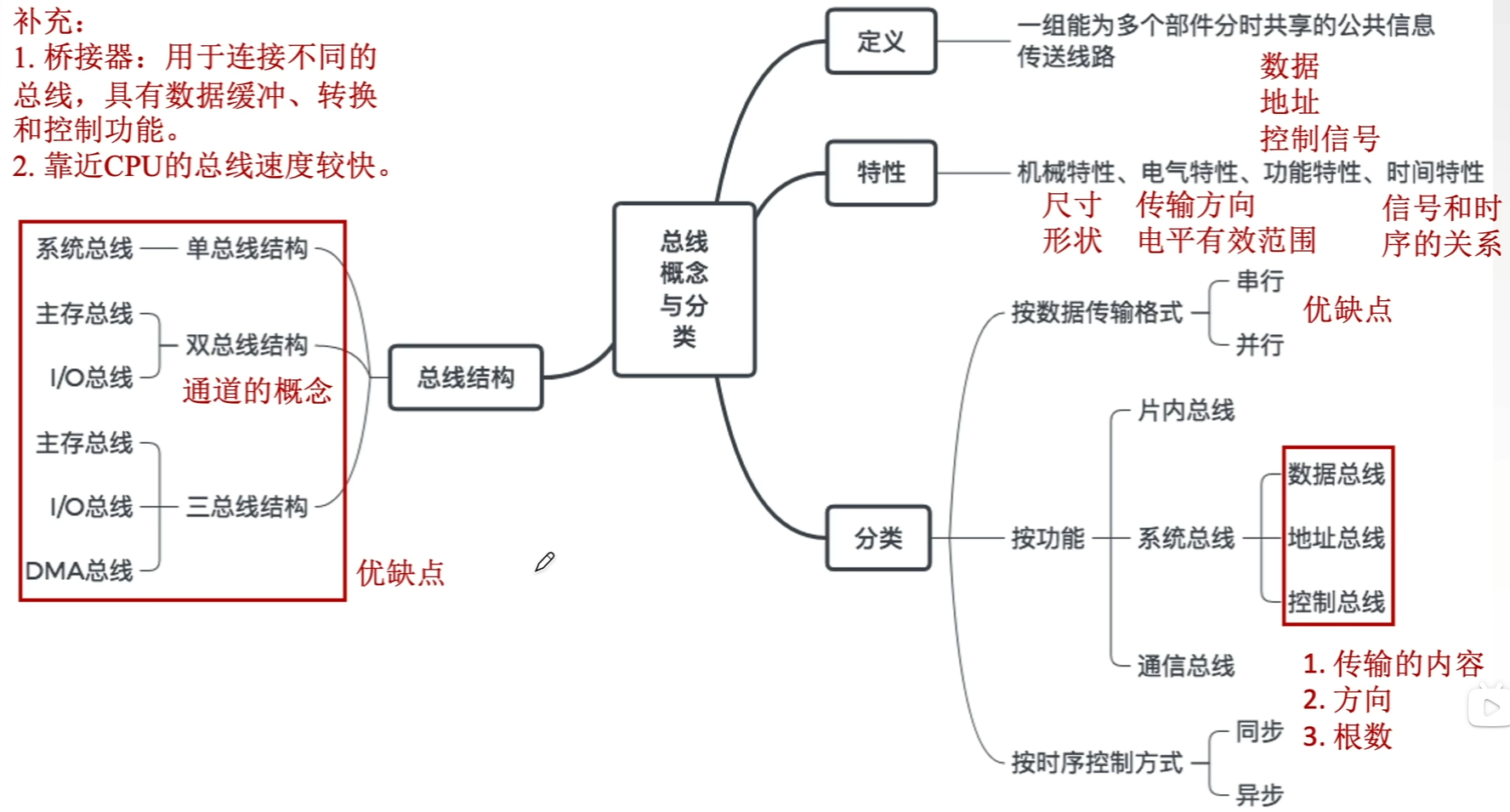
总线的特点
- 总线是一组能为多个部件分时共享的公共信息的传送线路。
- 分时是指同一时刻只允许有一个部件向总线发送信息,如果系统中有多个部件,则它们只能分时地向总线发送信息。
- 共享是指总线上可以挂接多个部件,各个部件之间互相交换的信息都可以通过这组线路分时共享。
- 早期计算机外部设备少时大多采用分散连接方式,不易实现随时增减外部设备。为了更好地解决I/O设备和主机之间连接的灵活性问题,计算机的结构从分散连接发展为总线连接。
总线的特性
- 机械特性:尺寸、形状、管脚数、排列顺序
- 电气特性:传输方向和有效的电平范围
- 功能特性:每根传输线的功能(地址、数据、控制)
- 时间特性:信号的时序关系
总线的分类
数据通路表示的是数据流经的路径,数据总线是承载的媒介。
按数据传输格式
设备通过串行总线只能一位一位地传输数据,通过并行总线可以同时传输多位数据。
- 串行总线:
- 优点:只需要一条传输线,成本低廉,广泛应用于长距离传输;应用于计算机内部时,可以节省布线空间。
- 缺点:在数据发送和接收的时候要进行拆卸和装配,要考虑串行-并行转换的问题。
- 并行总线:
- 优点:总线的逻辑时序比较简单,电路实现起来比较容易。
- 缺点:信号线数量多,占用更多的布线空间;远距离传输成本高昂;由于工作频率较高时,并行的信号线之间会产生严重干扰,对每条线等长的要求也越高,所以无法持续提升工作频率。
- 速度对比:
- 工作频率相同时,串行总线传输速度比并行总线慢。
- 并行总线的工作频率无法持续提高,而串行总线可以通过不断提高工作频率来提高传输速度,最终超过并行总线。
按总线功能
- 片内总线:片内总线是芯片内部的总线。它是CPU芯片内部寄存器之间、寄存器与ALU之间的公共连接线。
- 系统总线:系统总线是计算机系统内各功能部件(CPU、主存、I/O接口)之间相互连接的总线。按系统总线传输信息内容的不同,又可分为3类:数据总线、地址总线和控制总线。
-
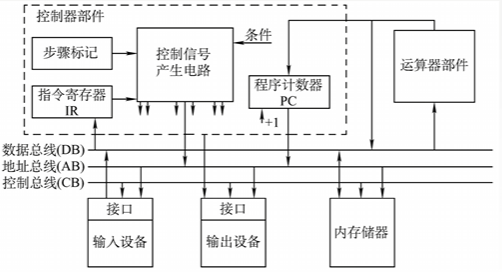
- 数据总线用来传输各功能部件之间的数据信息,它是双向传输总线,其位数与机器字长、存储字长有关。
- 地址总线用来指出数据总线上的源数据或目的数据所在的主存单元或I/O端口的地址,它是单向传输总线,地址总线的位数与主存地址空间的大小有关。
- 控制总线传输的是控制信息,包括CPU送出的控制命令和主存(或外设)返回CPU的反馈信号。
-
- 通信总线:通信总线是用于计算机系统之间或计算机系统与其他系统(如远程通信设备、测试设备)之间信息传送的总线,通信总线也称为外部总线。
系统总线的结构
-
单总线结构:CPU、主存、I/O设备(通过I/O接口)都连接在一组总线上,允许I/O设备之间、I/O设备和CPU之间或I/O设备与主存之间直接交换信息。
注:单总线并不是指只有一根信号线,系统总线按传送信息的不同可以细分为地址总线、数据总线和控制总线。
-
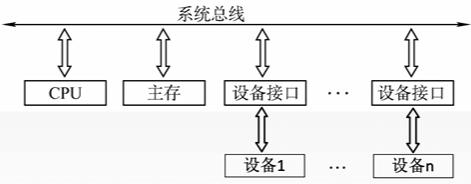
- 优点:结构简单,成本低,易于接入新的设备。
- 缺点:带宽低、负载重,多个部件只能争用唯一的总线,且不支持并发传送操作。
-
-
双总线结构:有两条总线,一条是主存总线,用于CPU、主存和通道之间进行数据传送;另一条是I/O总线,用于多个外部设备与通道之间进行数据传送。
-
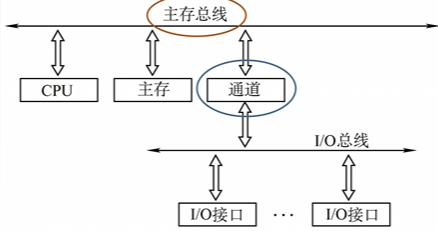
- 通道是具有特殊功能的处理器,能对I/O设备进行统一管理。通道程序放在主存中。
- 优点:将较低速的I/O设备从单总线上分离出来,实现存储器总线和I/O总线分离。支持突发(猝发)传送,即送出一个地址,收到多个地址连续的数据。
- 缺点:需要增加通道等硬件设备。
-
-
三总线结构:三总线结构是在计算机系统各部件之间采用3条各自独立的总线来构成信息通路,这3条总线分别为主存总线、I/O总线和直接内存访问DMA总线。
DMA: Direct Memory Access 直接内存访问
-
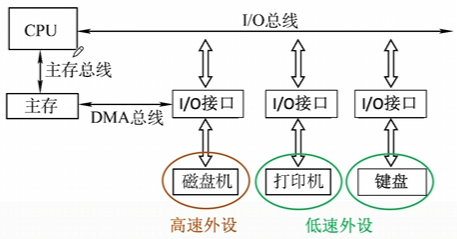
- 优点:提高了I/O设备的性能,使其更快地响应命令,提高系统吞吐量。
- 缺点:系统工作效率较低(三条总线只能同时工作一条)。
-
7.2 总线的性能指标
传输周期(总线周期)
- 一次总线操作所需的时间(包括申请阶段、寻址阶段、传输阶段和结束阶段),通常由若干个总线时钟周期构成。
时钟周期
-
即机器的时钟周期。计算机有一个统一的时钟,以控制整个计算机的各个部件,总线也要受此时钟的控制。
总线周期与总线时钟周期的关系比较魔幻,大多数情况下,一个总线周期包含多个总线时钟周期。有时候,一个总线周期就是一个总线时钟周期。有时候,一个总线时钟周期可包含多个总线周期。
工作频率
- 总线上各种操作的频率,为总线周期的倒数。若总线周期=N个时钟周期,则总线的工作频率=时钟频率/N。实际上指一秒内传送几次数据。
时钟频率
- 即机器的时钟频率,为时钟周期的倒数。若时钟周期为T,则时钟频率为 。实际上指一秒内有多少个时钟周期。
总线宽度
又称为总线位宽,它是总线上同时能够传输的数据位数,通常是指数据总线的根数,如32根称为32位(bit)总线。
总线带宽
可理解为总线的数据传输率,即单位时间内总线上可传输数据的位数,通常用每秒钟传送信息的字节数来衡量,单位可用字节/秒(B/s)表示。
总线带宽是指总线本身所能达到的最高传输速率。在计算实际的有效数据传输率时,要用实际传输的数据量除以耗时。
总线复用
总线复用是指一种信号线在不同的时间传输不同的信息。可以使用较少的线传输更多的信息,从而节省了空间和成本。
例题
同步总线采用数据线和地址线复用方式,其中地址/数据线有32根,总线时钟频率为66MHz,每个时钟周期传送两次数据(上升沿和下降沿各传送一次数据)。
1)该总线的最大数据传输率(总线带宽)是多少?
2)若该总线支持突发(猝发)传输方式,传输一个地址占用一个时钟周期,则一次“主存写”总线事务传输128位数据所需要的时间至少是多少?
(1)"数据线和地址线复用方式"即地址线先用这32根进行传输,数据线再分时复用
"每个时钟周期传送两次数据"即一个时钟周期包含两个总线周期,总线工作频率是时钟频率的两倍, $总线宽度=
(2)突发传输方式:一次总线事务中,主设备只需给出一个首地址,从设备就能从首地址开始的若干连续单元读出或写入多个数据。
发送首地址占用1个时钟周期,128位数据需传输4次,占用2个时钟周期
一个时钟周期 = 1/66MHz ≈ 15ns 总耗时 = (1+2) × 15ns = 45ns
7.3.1 程序查询方式

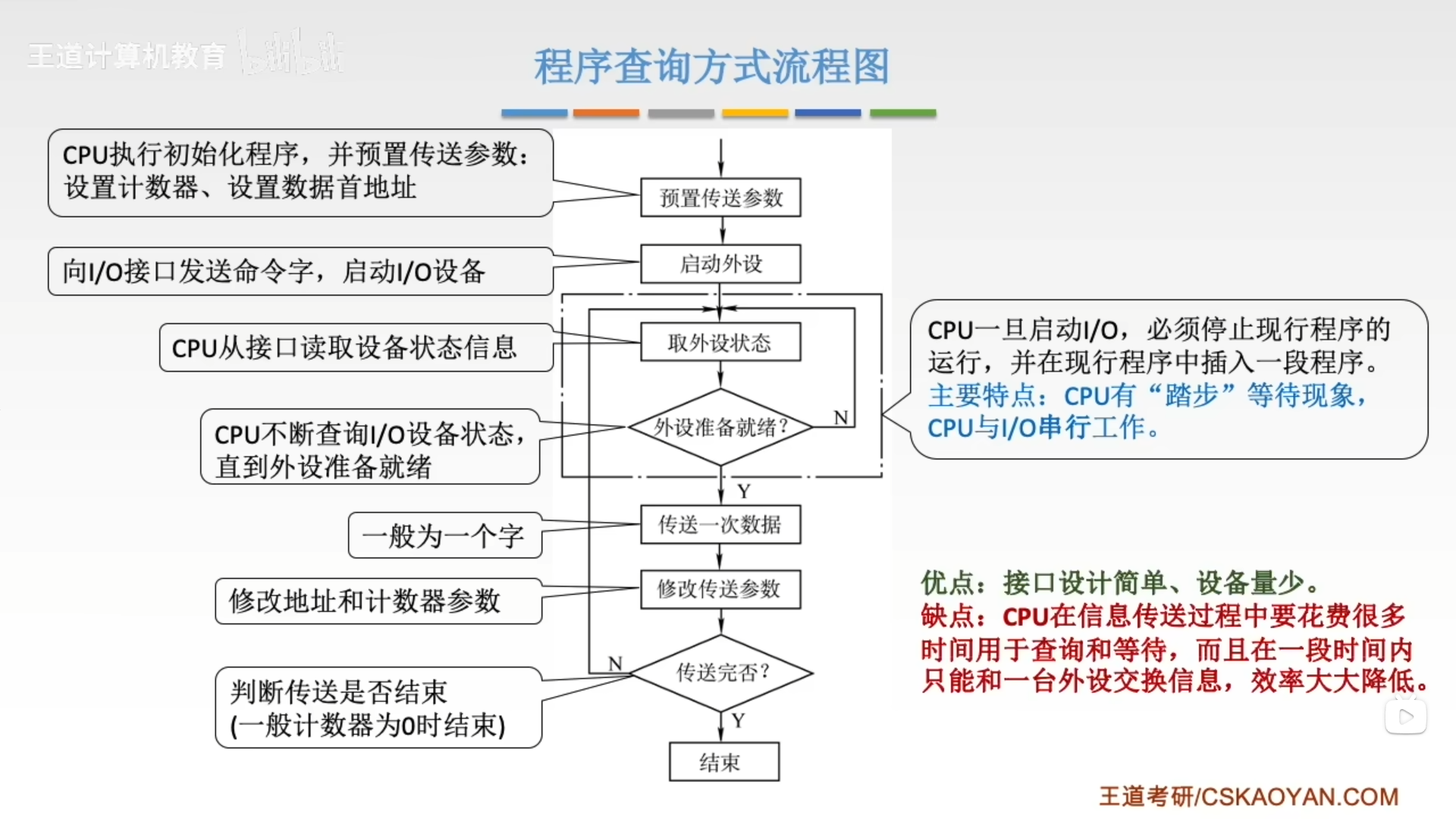
- 独占查询:CPU 100%的时间都在查询I/O状态,完全串行
- 定时查询:在保证数据不丢失的情况下,每隔一段时间CPU就查询一次I/O状态,查询的间隔内CPU可以执行其它程序
例题
-
在程序查询方式的输入/输出系统中,假设不考虑处理时间,每一个查询操作需要100个时钟周期,CPU的时钟频率为50MHz。现有鼠标和硬盘两个设备,而且CPU必须每秒对鼠标进行30次查询,硬盘以32位字长为单位传输数据,即每32位被CPU查询一次,传输率为。求CPU对这两个设备查询所花费的时间比率,由此可得出什么结论?
通过时钟频率得出一个时钟周期为
则每次查询操作耗时
(1)每秒查询鼠标耗时
查询鼠标所花费的时间比率
则对鼠标的查询基本不影响CPU的性能
(2)每32位需要查询一次,每秒传送
每秒需要查询
查询硬盘耗时
查询硬盘所花费的时间比率
则CPU将全部时间都用于硬盘的查询也不能满足硬盘传输的要求

