数据挖掘

数据挖掘复习

内容来自PPT及最后课上画的重点信息

复习题PPT

数据挖掘中的关联规则挖掘主要用来发现数据项之间的什么关系？

关联规则挖掘主要用来发现数据项之间的频繁共存或隐含的关联关系。

聚类分析中，K-means算法的K值表示什么？

在K-means聚类算法中，K值表示用户期望将数据集划分成的簇的数量。

决策树有哪些算法？主要根据什么标准选择特征进行划分，并分析各标准的不足之处。

算法	标准	不足
ID3	信息增益	强烈偏好多值特征，容易过拟合
C4.5	信息增益率	计算更复杂，可能偏好少值特征
CART	基尼指数	对多值特征有轻微偏好，倾向于不平衡分裂

给定一个简单的文本分类训练集，用于判断邮件是否为“垃圾邮件(Spam)”。词典包含以下5个词语：
["deal", "money", "urgent", "meeting", "free"]

训练数据：

• 垃圾邮件 (Spam, S)：
  1. “deal free money”
  2. “urgent free deal”
  3. “money urgent free”
• 非垃圾邮件 (Ham, H)：
  1. “meeting deal”
  2. “urgent meeting”

待分类的新邮件内容为：
“free urgent meeting”

任务要求：
使用多项式朴素贝叶斯模型（应用拉普拉斯平滑，其中平滑参数 λ=1λ=1）对该邮件进行分类。请按步骤完成以下计算：

1. 计算先验概率 P(Spam)P(Spam) 和 P(Ham)P(Ham)。

   文档总数：
   $N_{\text{doc}} = 3 + 2 = 5$

   $P(S) = \frac{3}{5} = 0.6$
   $P(H) = \frac{2}{5} = 0.4$

   先验概率结果：
   $P(S) = 0.6, \quad P(H) = 0.4$

2. 计算每个词语在 Spam 和 Ham 类别下的类条件概率。

   词典大小 $|V| = 5$

   Spam:

   deal: 2, money: 2, urgent: 2, meeting: 0, free: 3

   • 总词数：$2+2+2+0+3 = 9$
   • 分母：$9 + 5 = 14$

   $P(\text{deal}|S) = \frac{2+1}{14} = \frac{3}{14}$
   $P(\text{money}|S) = \frac{2+1}{14} = \frac{3}{14}$
   $P(\text{urgent}|S) = \frac{2+1}{14} = \frac{3}{14}$
   $P(\text{meeting}|S) = \frac{0+1}{14} = \frac{1}{14}$
   $P(\text{free}|S) = \frac{3+1}{14} = \frac{4}{14}$

   Ham:

   • deal: 1, money: 0, urgent: 1, meeting: 2, free: 0

   • 总词数：$1+0+1+2+0 = 4$

   • 分母：$4 + 5 = 9$

   $P(\text{deal}|H) = \frac{1+1}{9} = \frac{2}{9}$
   $P(\text{money}|H) = \frac{0+1}{9} = \frac{1}{9}$
   $P(\text{urgent}|H) = \frac{1+1}{9} = \frac{2}{9}$
   $P(\text{meeting}|H) = \frac{2+1}{9} = \frac{3}{9}$
   $P(\text{free}|H) = \frac{0+1}{9} = \frac{1}{9}$

3. 将新邮件 “free urgent meeting” 表示为词频向量。

   "free urgent meeting"的词频向量（按词典顺序：deal, money, urgent, meeting, free）：
   $[0, 0, 1, 1, 1]$

4. 计算该邮件属于 Spam 和 Ham 的后验概率。

   Spam:

   $P(S|d) \propto P(S) \times P(\text{urgent}|S) \times P(\text{meeting}|S) \times P(\text{free}|S)$
   $= 0.6 \times \frac{3}{14} \times \frac{1}{14} \times \frac{4}{14}$
   $= 0.6 \times \frac{12}{2744} \approx 0.002624$

   Ham:

   $P(H|d) \propto P(H) \times P(\text{urgent}|H) \times P(\text{meeting}|H) \times P(\text{free}|H)$
   $= 0.4 \times \frac{2}{9} \times \frac{3}{9} \times \frac{1}{9}$
   $= 0.4 \times \frac{6}{729} \approx 0.003292$

   归一化:

   $P(S|d) = \frac{0.002624}{0.002624 + 0.003292} \approx 0.444$
   $P(H|d) = \frac{0.003292}{0.002624 + 0.003292} \approx 0.556$

5. 根据后验概率判断其最终类别。

   由于 $P(H|d) > P(S|d)$，新邮件被分类为：

   $\boxed{Ham}$

2.1.4 属性的类型

标称、序数、区间、比率

属性类型		描述	例子	操作
分类 (定性)	标称	标称属性的值仅仅只是不同的名字，即标称值只提供足够的信息以区分对象（=，≠）	邮政编码，雇员ID号，性别	众数、熵、列联相关，卡方检验
	序数	序数属性的值提供足够的信息确定对象的序（<>）	矿石硬度{好，一般}、成绩等级、街道号码	中值、百分位、秩相关、游程检验、符号检验
数值 (定量)	区间	对于区间属性，值之间的差是有意义的，即存在测量单位（+，-）	日历日期、摄氏或华氏温度	均值、标准差、皮尔逊相关系数，t和F检验
	比率	对于比率属性，差和比率都是有意义的（+，-，*，/）	绝对温度、货币量、计数、年龄、质量、长度、电流	几何平均、调和平均、百分比变差

2.2.1 中心化趋势

均值、中位数和众数

$Mean-mode = 3 * (mean - median)$

2.2.2 四分位极差

第一个四分位数，即第25百分位上的数据 $(n-1)/4$ （仅对于第一个四分位数，若是第三个四分位数还要乘3）

若n为偶数 需要$+0.25\times (d_{n+1}-d_n)$ （仅对于第一个四分位数，若是第三个四分位数就是0.75）

2.4.4 数值属性的近邻性度量

两个 $p$ 维变量 $x_1 = \{x_{11}, x_{12}, \ldots, x_{1p}\}$ 和 $x_2 = \{x_{21}, x_{22}, \ldots, x_{2p}\}$ 间的闵可夫斯基距离定义为：

$$d(i,j) = \sqrt[q]{|x_{i1} - x_{j1}|^q + |x_{i2} - x_{j2}|^q + \cdots + |x_{ip} - x_{jp}|^q}$$

当 $q=1$ 时，表示曼哈顿距离：

$$d(i,j) = |x_{i1} - x_{j1}| + |x_{i2} - x_{j2}| + \cdots + |x_{ip} - x_{jp}|$$

当 $q=2$ 时，表示欧式距离：

$$d(i,j) = \sqrt{|x_{i1} - x_{j1}|^2 + |x_{i2} - x_{j2}|^2 + \cdots + |x_{ip} - x_{jp}|^2}$$

当 $q \to \infty$ 时，表示切比雪夫距离：

$$d(i,j) = \lim_{q \to \infty} \left( \sum_{k=1}^p |x_{ik} - x_{jk}|^q \right)^{\frac{1}{q}} = \max_{1 \le k \le p} |x_{ik} - x_{jk}|$$

n欧几里得和曼哈顿距离满足以下数学性质

• 正定性：距离是一个非负数 d(i,j)>0, 如果i≠j d(i,i)=0

• 对称性：d(i,j)=d(j,i)

• 三角不等式

2.4.8 余弦相似度

余弦相似度可以用来比较文档的相似性

$$s(x, y) = \frac{x^T y}{\|x\|_2 \|y\|_2} \quad x = [1, 1, 0, 0] \quad y = [0, 1, 1, 0]$$

$$s(x, y) = \frac{0 + 1 + 0 + 0}{\sqrt{2} \sqrt{2}} = 0.5$$

3.2 数据预处理

• 数据清理

  • 填写缺失值，平滑噪声数据、识别或删除离群点，并解决不一致问题

• 数据集成

  • 整个多个数据库，多维数据集或文件

• 数据缩减

  • 降维、数据压缩、Numerosity Reduction

• 数据转换和数据离散化

  • 正常化
  • 生成概念层次结构

3.2.1 如何处理缺失数据

• 忽略元组
  • 当类标号缺失时，监督学习
  • 当每个属性缺失值比例较大时
• 手动填写缺失值，工作量较大
• 自动填写
  • 使用一个全局的常数
  • 使用属性的平均值填充空缺值
    • 属性全局平均值
    • 同一类数据对象的属性平均值
    • 最有可能的值：基于贝叶斯公式或决策树推理，回归、最近邻策略

3.2.4 相关分析

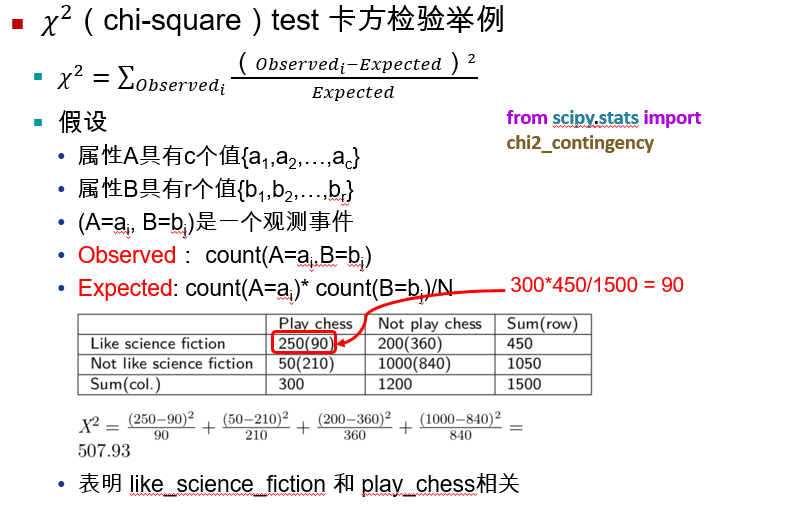
3.2.7 数据规约策略

• 为什么进行数据规约 data reduction?

  • 由于数据仓库可以存储TB级别的数据，因此在一个完整的数据集上运行时，复杂的数据分析可能需要很长的时间。

  • 通常，在数据预处理时需要对数据进行规约

  • 用较小的数据替换原数据

• 常见数据规约策略

  • 降维

  • 降数据

  • 数据压缩

3.2.8 特征降维

• PCA (Principal Component Analysis) 主成分分析方法
• 非负矩阵分解 (NMF)
• 线性判别分析 (Linear Discriminant Analysis ,LDA)

特征选择

• 从原始特征集合中选择一个代表性的特征子集

• 单特征重要性评估

• 基于模型的特征重要性评估

3.2.11 规范化

最小-最大规范化（Min-Max Normalization）

• 某属性 $A$ 从区间 $[\min_A, \max_A]$ 规范化到 $[new_{\min_A}, new_{\max_A}]$

  $$v' = \frac{v - \min_A}{\max_A - \min_A} (new_{\max_A} - new_{\min_A}) + new_{\min_A}$$

• 例子：将收入从 $12000$ 到 $98000$ 区间规范化到 $[0,1]$ 之间，$73600$ 规范后的值为？

Z-分数规范化（Z-score Normalization）

$$v' = \frac{v - \mu_A}{\sigma_A}$$

• 例子：属性 $A$ 的均值 $\mu_A = 54000$，标准差 $\sigma_A = 16000$，$73600$ 规范后的值为？

小数定标规范化

• 移动小数点的位置，移动位数依赖于属性 $A$ 的最大值，公式如下

  $$v' = \frac{v}{10^j}$$

• $j$ 为使 $\max(|v'|) < 1$ 的最小整数
• 例如：一组数据的最小值 $12000$，最大值为 $98000$，$j$ 值为 $5$

  $$[12000, 98000] \rightarrow [0.12, 0.98]$$

4.3.2 决策树构建

• 决策树(Decision Tree) ：从训练数据中学习得出一个树状结构的模型，它是一种以树状结构(包括二叉树和多叉树)形式来表达的预测分析模型
• 决策树是一种有监督学习的算法、属于判别模型
• 决策树又称为判定树，是数据挖掘技术中一种重要的分类与回归方法
• 决策树有两种:分类树和回归树
• 决策树学习通常包含3个步骤: 特征选择,决策树的生成,决策树的剪枝
• 常用的方法：ID3, C4.5, CART

4.5 KNN算法

• k近邻法(k-Nearest Neighbor, kNN)是一种比较成熟也是最简单的机器学习算法，可以用于基本的分类与回归方法。
• 算法的主要思路: 如果一个样本在特征空间中与𝑘个实例最为相似(即特征空间中最邻近)，那么这𝑘 个实例中大多数属于哪个类别，则该样本也属于这个类别。
• 𝑘近邻算法三要素: 𝑘值选择，距离度量，决策规则

KNN与K-Means的区别

K-NN是监督学习中的一种分类算法，类别是已知的，通过对已知分类的数据进行训练和学习，找到这些不同类的特征，再对未分类的数据进行分类。

K-Means是非监督学习中一种聚类算法，事先不知道数据会分为几类，通过聚类分析将数据聚合成几个群体。聚类不需要对数据进行训练和学习。

有监督学习和无监督学习

有监督学习是一种机器学习方法，其中使用标记数据进行训练。每个输入数据都有对应的输出标签，模型通过学习这些输入与输出之间的关系来进行预测。

• 特点：

  • 需要大量的标记数据。

  • 训练过程有明确的目标，模型可以通过反馈不断调整。

  • 常见算法包括线性回归、逻辑回归、支持向量机（SVM）、决策树等。

• 应用场景：

  • 适用于分类和回归问题，例如图像识别、语音识别和金融预测等。

无监督学习是一种机器学习方法，其中使用未标记的数据进行训练。模型从输入数据中自动发现模式和结构，而不依赖于任何标签。

• 特点：
  • 不需要标记数据，适合处理大量未标记的数据。
  • 训练过程没有明确的目标，模型通过数据的内在结构进行学习。
  • 常见算法包括聚类（如K均值）、关联规则学习（如Apriori算法）等。
• 应用场景：
  • 适用于数据聚类、市场细分、异常检测等。

5.3 基于密度的聚类方法

DBSCAN算法描述

• 输入：包含 $n$ 个对象的数据库，半径 $\varepsilon$ (Eps)，最少数目 MinPts

• 输出：所有生成的簇，达到密度要求

• Repeat

  • 从数据中抽取一个未处理过的点
  • If 抽出的点是核心点 Then 找出所有从该点密度可达的对象，形成一个簇
  • Else 抽出的点是边缘点（非核心对象），跳出本次循环，寻找下一点
  • EndIf

• Until 所有点被处理

核心对象:如果对象的ε-领域至少包含最小数目MinPts个对象，则称该对象为核心对象

边界点(Border point)的"Eps"(ε) 领域有少于MinPts个对象，但它的领域中有核心对象

6.1 混淆矩阵

混淆矩阵(Confusion Matrix)

实际类 \ 预测类	Class=Yes	Class=No
Class=Yes	a (TP)	b (FN)
Class=No	c (FP)	d (TN)

• $a+d$ 表示所有样本中被正确分类的样本数量
• $b+c$ 表示所有样本中被错误分类的样本数量
• $a+b+c+d$ 表示样本总数
• 准确率

$$Accuracy = \frac{a+d}{a+b+c+d} = \frac{TP+TN}{TP+TN+FP+FN}$$

• 召回率（查全率，recall）

  $$recall = \frac{TP}{TP+FN}$$

  • 表示样本中的正例被正确预测的比例，即有多少正例样本被预测正确了

• 精确率（查准率，precision）

  $$precision = \frac{TP}{TP+FP}$$

  • 表示预测的正例中被正确预测的比例，即预测为正例样本中有多少是真的正例

6.5 过拟合和欠拟合

导致过拟合的原因：

• 噪声：训练集中存在大量噪声数据

• 缺乏代表性样本：训练集规模较小，训练模型过于复杂

7.1 集成学习的优势

• 能够有效降低预测误差

  • 假设一个集成分类器包含3个单分类器，其中每个分类器的错误率为40%. C表示预测正确，I表示预测错误，Probability表示最终预测结果概率，总的组合数为23=8种

  • 模型的误差率为：0.096+0.096+0.096+0.064=35.2%<40%

  • 设模型数量为 $m$，模型的错误率为 $r$

  • 通用的误差计算公式为：

    $$p(error) = \sum_{i=(m+1)/2}^{m} C_{m}^{i} r^{i}(1-r)^{m-i}$$

    • $m$ 个模型中有超一半分类错误时→最终结果错误，$i$ 从 $(m+1)/2$ 到 $m$
    • 随机从 $m$ 中选择 $i$ 个，其余 $m-i$ 个分类正确
    • 下图为 $r=0.4$ 时误差率和模型规模的关系图